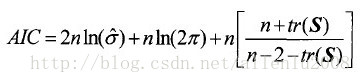作者：陈凤 (西安交通大学)
 
Stata连享会   计量专题 || 精品课程 || 简书推文 || 公众号合集

 

连享会计量方法专题……

 

文章目录

• • • • 连享会计量方法专题……
  • 1. 地理加权回归模型简介
  • 2. 地理加权回归模型的参数估计方法
  • • • 连享会计量方法专题……
  • 3. 常用的核函数
  • • 3.1. Gussian kernel function
    • 3.2. Bi-square kernel function
    • 3.3. K-nearest neighbor kernel function
  • 4. 窗宽h的选择准则
  • • 4.1. 交叉确认方法(Cross-validation (CV) criterion)
    • • 连享会计量方法专题……
    • 4.2. 广义交叉确认方法(Generalized cross-validation (GCV) criterion)
    • 4.3. AICc信息准则(Corrected Akaike information criterion (AICc))
    • • 连享会计量方法专题……
  • 4. 在 R 软件运行地理加权回归模型
  • 5. 参考文献
  • • • 关于我们

1. 地理加权回归模型简介

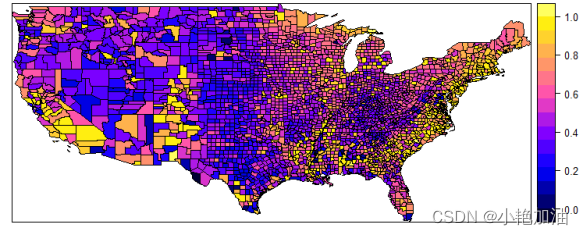
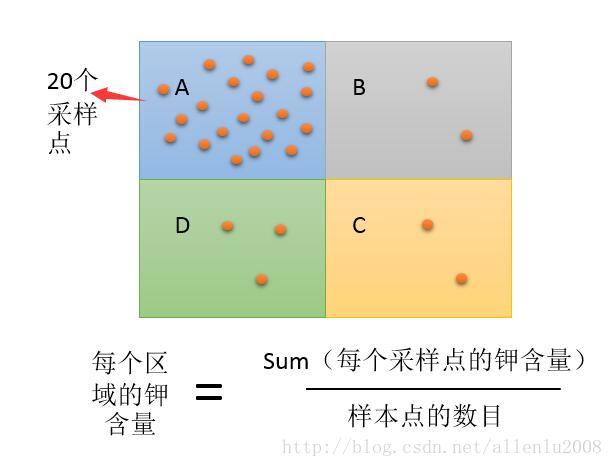
空间数据在地理学、经济学、环境学、生态学以及气象学等众多领域中广泛存在。根据 Tobler 提出的 「地理学第一定律」：任何事物之间都是空间相关的，距离越近的事物之间的空间相关性越大。因此，不同于传统的截面数据，空间数据的空间相关性会导致回归关系的空间非平稳性 (空间异质性)。为了探索空间数据的空间非平稳性， Brunsdon 等 (1996) 首次提出了 地理加权回归模型，设定如下：

$$Y_i={\beta }_0(u_i,v_i)+\sum _{j=1}^p{\beta }_j(u_i,v_i)X_{ij}+{\epsilon }_i\text{\hspace{1em}(1)}$$

其中，${\beta }_j(u,v)(j=0,1,\cdots ,p)$ 为 「空间地理位置函数」。

以某城市的房屋价格 $Y$ 和房屋面积 $X$ 为例， 如果不考虑房屋的地理位置信息，可以建立一个简单的线性回归模型：

$$Y_i=\beta X_i+{\epsilon }_i\text{\hspace{1em}(2)}$$

其中，$\beta$ 为房屋的单位面积均价。实际中，处于不同位置的房屋价格可能会相差甚远，但是模型 $(2)$ 却不能反映出这种异质性。因此，为了能够描述不同位置房屋价格的差异性，我们可以建立如下模型：

$$Y_i=\beta (u_i,v_i)X_i+{\epsilon }_i\text{\hspace{1em}(3)}$$

其中，$\beta (u,v)$ 是地理位置的函数。相比于模型 $(2)$，模型 $(3)$ 可以反映房屋价格随地理位置的变化而变化的规律。

上述例子说明有必要对空间数据建立地理加权回归模型来探索空间数据的非平稳性。

2. 地理加权回归模型的参数估计方法

根据 Tobler 地理学第一定律，距离越近的事物之间的相关性越大。故对于一个给定的地理位置$(u_0,v_0)$，可以采用局部加权最小二乘来估计 ${\beta }_j(u_0,v_0)(j=0,1,\cdots ,p)$，即

$$\min \sum _{i=1}^n[y_i-\sum _{j=1}^p{\beta }_j(u_0,v_0)x_{ij}{]}^2{w}_i(u_0,v_0)\text{\hspace{1em}(4)}$$

其中， { w i ( u 0 , v 0 ) } i = 1 n \{w_i(u_0,v_0)\}_{i=1}^n {wi​(u0​,v0​)}i=1n​ 是在地理位置 $(u_0,v_0)$ 处的空间权重。令 $\mathbf{\beta }(u_0,v_0)=({\beta }_0(u_0,v_0),{\beta }_1(u_0,v_0),\cdots ,{\beta }_p(u_0,v_0){)}^{\mathrm{T}},$ 则 $\mathbf{\beta }(u_0,v_0)$ 在 $(u_0,v_0)$ 处的局部最小二乘估计值为

$$\hat{\mathbf{\beta }}(u_0,v_0)={\left({\mathbf{X}}^{\mathrm{T}}\mathbf{W}(u_0,v_0)\mathbf{X}\right)}^{-1}{\mathbf{X}}^{\mathrm{T}}\mathbf{W}(u_0,v_0)\mathbf{Y}\text{\hspace{1em}(5)}$$

其中，

$$\mathbf{X}=({\mathbf{X}}_0,{\mathbf{X}}_1,\cdots ,{\mathbf{X}}_p),{\mathbf{X}}_j=(x_{1j},x_{2j},\cdots ,x_{nj}{)}^{\mathrm{T}};$$

$$\mathbf{Y}=(Y_1,Y_2,\cdots ,Y_n{)}^{\mathrm{T}};$$

$$\mathbf{W}(u_0,v_0)=\mathrm{D}\mathrm{i}\mathrm{a}\mathrm{g}\left(w_1(u_0,v_0),w_2(u_0,v_0),\cdots ,w_n(u_0,v_0)\right).$$

令 $(u_0,v_0)=(u_i,v_i),i=1,2,\cdots ,n$，则可以由公式 $(5)$ 得到回归函数 $\mathbf{\beta }(u,v)$在所有观测位置处的局部估计值。

注1： ${\beta }_j(u,v)(j=0,1,\cdots ,p)$ 可以在任意位置处被估计。因此，GWR 模型也可以作为空间数据的插值工具。
注2： 在 $(u_0,v_0)$ 处，$\mathbf{\beta }(u_0,v_0)$ 的 GWR 估计值和如下线性模型的最小二乘估计是等价的：

$$\sqrt{w_i(u_0,v_0)}{Y}_i=\sum _{j=1}^p\sqrt{w_i(u_0,v_0)}{x}_{ij}{\beta }_j(u_0,v_0)+{\bar{\epsilon }}_i,i=1,2,\cdots ,n.\text{\hspace{1em}(6)}$$

 

连享会计量方法专题……

3. 常用的核函数

在核光滑方法中，常用的核函数如下：

3.1. Gussian kernel function

$$w_i(u_j,v_j)=K_h(d_{ij})=\frac{1}{\sqrt{2\pi }}\exp \left(-\frac{1}{2}{\left(\frac{d_{ij}}{h}\right)}^2\right),$$

其中，$h$ 为窗宽，$d_{ij}$ 为点 $(u_i,v_i)$ 和 $(u_j,v_j)$ 之间的距离。

3.2. Bi-square kernel function

$$w_i(u_j,v_j)=K_h(d_{ij})=\{\begin{array}{rc}{\left[1-{\left(\frac{d_{ij}}{h}\right)}^2\right]}^2,& \left|d_{ij}\right|<h;\\ 0,& \left|d_{ij}\right|>h.\end{array}$$

给一个$h$，$(u_i,v_i)$处自变量的观测值对$(u_0,v_0)$处因变量的权重$w_i(u_0,v_0)$如下所示。

3.3. K-nearest neighbor kernel function

给定$K$，$d_{ik}$为$(u_i,v_i)$到第$K$个邻近点的距离，则

$$w_i(u_j,v_j)=K_h(d_{ij})=\{\begin{array}{rc}{\left[1-{\left(\frac{d_{ij}}{d_{ik}}\right)}^2\right]}^2,& \left|d_{ij}\right|<d_{ik};\\ 0,& \left|d_{ij}\right|>d_{ik}.\end{array}$$

对于任意的观测点来说，$K$近邻核函数总是保持有$K$个观测点的空间权重不为零，如下所示。

4. 窗宽h的选择准则

在地理加权回归模型中，常用的最优窗宽选取准则有交叉确认方法、广义交叉确认方法以及AICc信息准则。这三种准则的定义分别如下所示。

4.1. 交叉确认方法(Cross-validation (CV) criterion)

交叉确认方法的具体过程如下：给定一个 $h$, 去掉第 $i$ 组观测值 $(Y_i,X_i)$，用剩下的 $(n-1)$ 组数据在给定的 $h$下进行地理加权回归参数估计，然后得到在 $X_i$ 处的拟合值${\hat{Y}}_{(-i)}(h)$。令

$$\mathrm{C}\mathrm{V}(h)=\frac{1}{h}\sum _{i=1}^n{\left(Y_i-{\hat{Y}}_{(-i)}(h)\right)}^2,$$

则最优窗宽 $h_0$ 的选取如下：

$$h_0=\arg \underset{h>0}{\min }\mathrm{C}\mathrm{V}(h)$$

 

连享会计量方法专题……

4.2. 广义交叉确认方法(Generalized cross-validation (GCV) criterion)

设

$$\hat{\mathbf{Y}}(h)={\left({\hat{Y}}_1(h),{\hat{Y}}_2(h),\cdots ,{\hat{Y}}_n(h),\right)}^{\mathrm{T}}=\mathbf{L}(h)\mathbf{Y},$$

其中，$\mathbf{L}(h)$ 为 “帽子” 矩阵，令

$$\mathrm{G}\mathrm{C}\mathrm{V}(h)=\frac{n}{{\left(n-tr(\mathbf{L}(h))\right)}^2}\sum _{i=1}^n{\left(Y_i-{\hat{Y}}_i(h)\right)}^2,$$

则最优窗宽 $h_0$ 的选择标准为：

$$h_0=\arg \underset{h>0}{\min }\mathrm{G}\mathrm{C}\mathrm{V}(h)$$

4.3. AICc信息准则(Corrected Akaike information criterion (AICc))

令 $\hat{\mathbf{Y}}(h)=\mathbf{L}(h)\mathbf{Y}$， $\hat{\mathbf{\epsilon }}={\mathbf{Y}}^{\mathrm{T}}({\mathbf{I}}_n-\mathbf{L}(h){)}^{\mathrm{T}}({\mathbf{I}}_n-\mathbf{L}(h))\mathbf{Y}$，则有

$$\mathrm{A}\mathrm{I}\mathrm{C}\mathrm{c}(h)=\log \left(\frac{1}{n}{\hat{\mathbf{\epsilon }}}^{\mathrm{T}}\hat{\mathbf{\epsilon }}\right)+\frac{n+tr(\mathbf{L}(h))}{n-2-tr(\mathbf{L}(h))}.$$

最优窗宽 $h_0$ 的选取如下：

$$h_0=\arg \underset{h>0}{\min }\mathrm{A}\mathrm{I}\mathrm{C}\mathrm{c}(h)$$

$\mathrm{A}\mathrm{I}\mathrm{C}\mathrm{c}$ 准则选择最优窗宽如下所示：

注：模拟实验以及经验表明，$\mathrm{C}\mathrm{V}$ 和 $\mathrm{G}\mathrm{C}\mathrm{V}$ 准则一般会趋于确定一个稍微偏小的窗宽$h_0$，而较小的窗宽会使得回归函数的估计值偏差减小，但是方差会增大。因此，会出现过拟合现象。但是对于 $\mathrm{A}\mathrm{I}\mathrm{C}\mathrm{c}$ 在很多情况下可以较好的克服过拟合现象，即趋于确定一个更合理的窗宽。

 

连享会计量方法专题……

4. 在 R 软件运行地理加权回归模型

在R软件中，可以调用 Rpacakge-GWmodel (Lu, B. B, et al. 2014) 来实现地理加权回归模型的参数过程。以都柏林 2014 年的选举数据为例，下面介绍 GWR 在 R 中的实现过程：

# 1. 加载 Rpacakge：
library("GWmodel")# 2. 加载数据
data(DubVoter)# 3. 选择最优窗宽
Dub<cbind(Dub.voter\$DiffAdd,Dub.voter\$LARent,Dub.voter\$SC1,Dub.voter\$Unempl,Dub.voter\$LowEduc,Dub.voter\$Age18_24,Dub.voter\$Age25_44,Dub.voter\$Age45_64,Dub.voter\$GenEl2004)
DubCoord<-cbind(Dub.voter\$X,Dub.voter\$Y) %地理位置
DIS<-gw.dist(dp.locat=DubCoord)% 计算距离矩阵
bw1<bw.gwr(GenEl2004~DiffAdd+LARent+SC1+Unempl+LowEduc+Age18_24+Age25_44+Age45_64, approach="AICc",adaptive=TRUE, data=Dub.voter, kernel = "bisquare",dMat=DIS) %选择bi-square函数作为核函数，使用AICc准则选择最优窗宽# 4. 拟合GWR模型
gwr.res1<gwr.basic(GenEl2004~DiffAdd+LARent+SC1+Unempl+LowEduc+Age18_24+Age25_44+Age45_64, data=Dub.voter, bw=bw1,adaptive=TRUE,kernel = "bisquare", dMat=DIS)# 5. 将局部估计值画在对应的地图上面
library("RColorBrewer")
Mcolor<-1;mypalette <- colorRampPalette(brewer.pal(9, "Greys"))(200)
map.na=list("SpatialPolygonsRescale", layout.north.arrow(),offset=c(329000, 261500), scale=4000,col=1)
map.scale.1=list("SpatialPolygonsRescale",layout.scale.bar(),offset=c(326500, 217000), scale=5000,col=1,fill=c("transparent","black"))
map.scale.2=list("sp.text",c(326500, 217900),"0",cex=0.9,col=1)
map.scale.3=list("sp.text",c(331500, 217900),"5km",cex=0.9,col=1)             
map.layout<-list(map.na,map.scale.1,map.scale.2,map.scale.3)
mypalette.9<-brewer.pal(9,"Greys")
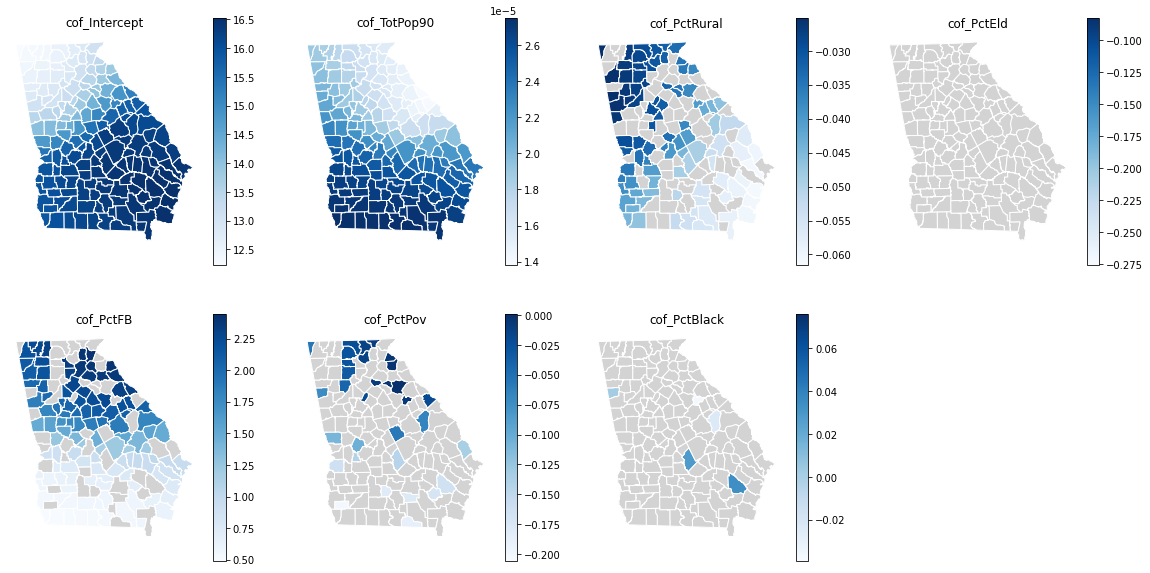
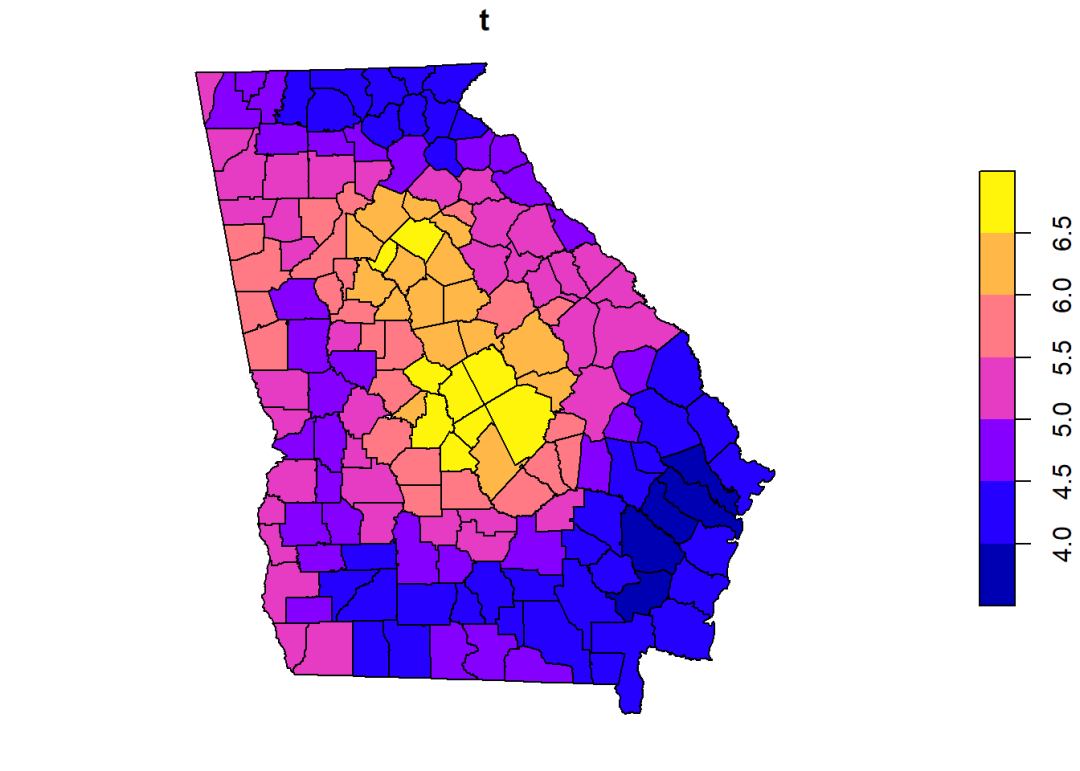
spplot(gwr.res1$SDF, "LowEduc",key.space="right",col.regions=mypalette.6, at=c(-8,-6,-4,-2,0,2,4),sp.layout=map.layout)

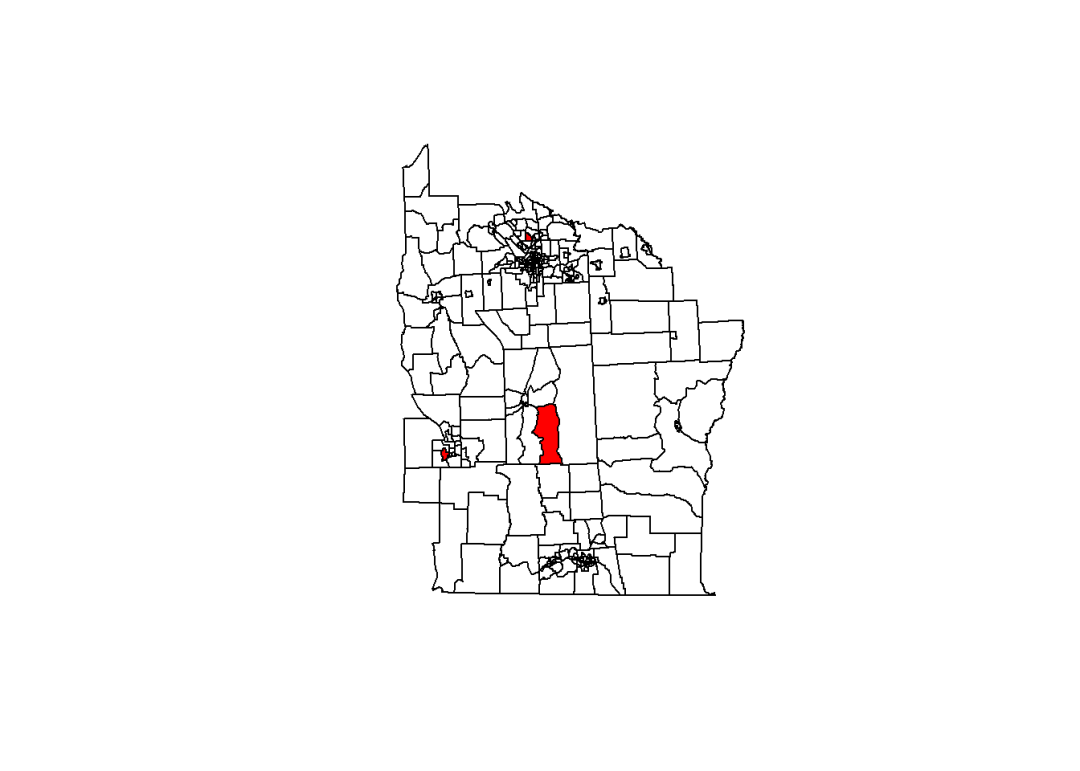
在都柏林 2014 年选择数据中，使用 AICc 准则确定的最优窗宽为 115，其中变量 LowEduc 的回归系数的局部估计值如下：

5. 参考文献

• Brunsdon, C. E, Fotheringham, A. S. and Charlton, M. E., 1999. Some notes on parametric significance test for geographically weighted regression. Journal of Regional Science, 39 (3): 497–524. [PDF]
• 梅长林, 王宁. 近代回归分析方法 [M]: 北京：科学出版社, 2012.
• Lu, B. B., Harris, P., Charlton, M. and Brunsdon, C., 2014. The GWmodel R package: further topics for exploring spatial heterogeneity using geographically weighted models. Geo-spatial Information Science, 17 (2): 85–101. [PDF]

 

关于我们

• 「Stata 连享会」 由中山大学连玉君老师团队创办，定期分享实证分析经验， 公众号：StataChina。
• 公众号推文同步发布于 CSDN 、简书 和 知乎Stata专栏。可在百度中搜索关键词 「Stata连享会」查看往期推文。
• 点击推文底部【阅读原文】可以查看推文中的链接并下载相关资料。
• 欢迎赐稿： 欢迎赐稿。录用稿件达 三篇 以上，即可 免费 获得一期 Stata 现场培训资格。
• E-mail： StataChina@163.com
• 往期推文：计量专题 || 精品课程 || 简书推文 || 公众号合集

---