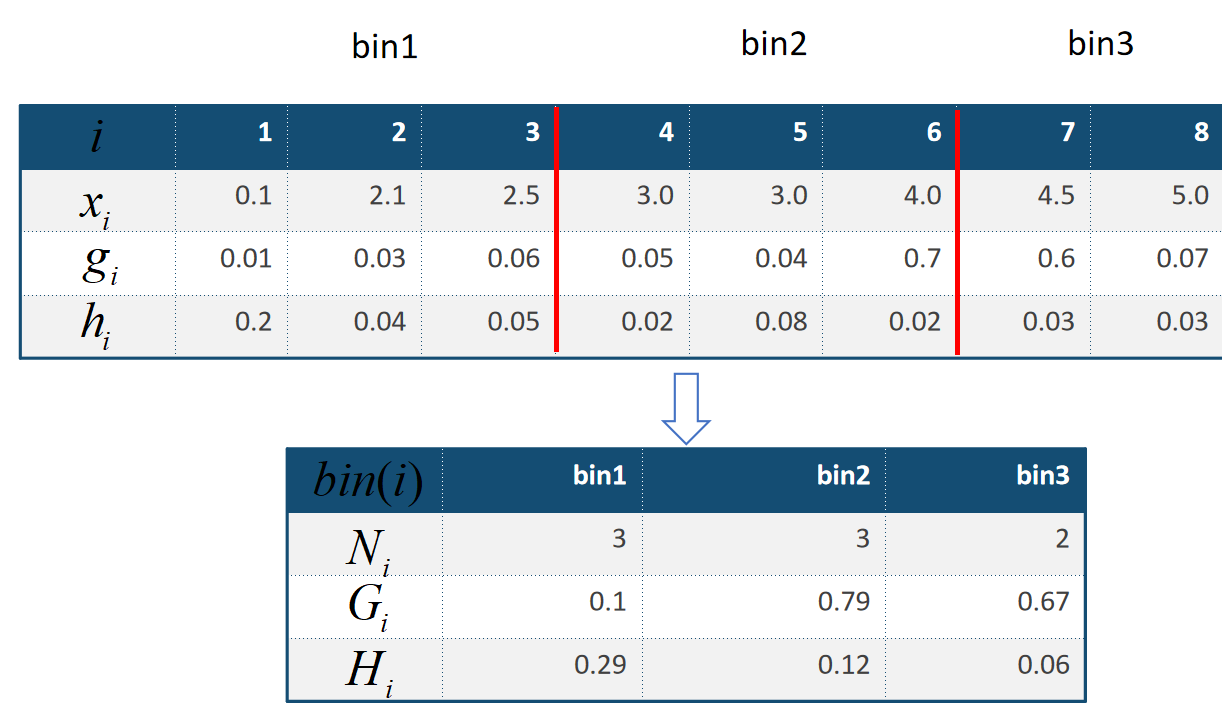
决策树ID3，C4.5是多叉树，CART树是一个完全二叉树，CART树不仅能完成分类也能实现回归功能，所谓回归指的是目标是一个连续的数值类型，比如体重、身高、收入、价格等，在介绍ID3，C4.5其核心是信息熵的应用，而在实际应用中熵的运算会涉及大量的对数运算，其复杂度还是比较高的。CART树采用了一个与熵近似的概念'基尼系数',不同于熵来自于物理学，基尼系数来自于经济学范畴，原本是用来衡量国民收入是否平均：当基尼系数为0时代表收入平均，而大于0.5时代表贫富差异显著。在决策树模型中，基尼系数越高代表信息纯度越低，基尼系数越低代表纯度越高，而纯度的高低代表样本数据不确定性的大小，这方面来说基尼系数与熵的功效一致，实际上基尼系数在是信息熵的近似，可以观察下图:

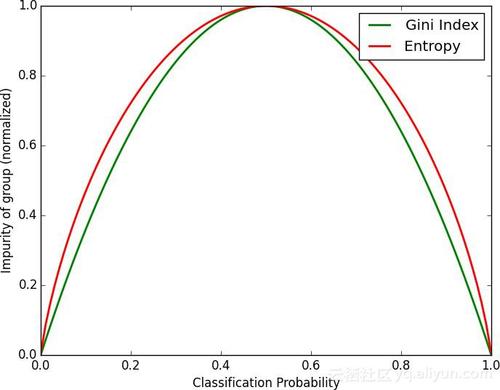
上图中红色曲线代表信息熵，绿色曲线代表基尼系数，可以看到两者走势是一样的。基尼系数是初等函数二次多项式的运算，这比熵的对数运算简单多了。如果要问CART树能不能用熵来代替基尼系数呢？答案是当然可以了，熵更能反映出信息的不确定性，香农博士的理论可不是开玩笑的，但是接下来了解算法特性后就会发现如果用熵来构建CART树，计算量将会非常之大，选用基尼系数是平衡准确率与效率之后的折中之举，这个折中的办法其实不会降低CART树的实际效果，在介绍ID3，C4.5结尾时曾提到，决策树本质是一个弱分类器，实际应用中不会单独用一棵决策树来实现分类的，而是会用集成算法将多棵决策树汇总起来进行运算。这里涉及相关知识有Bagging，Boosting 集成算法以及随机森林、GBDT梯度下降树等，这些都将在以后篇章中详细介绍。

一、CART树实现分类

2.1、CART树分类原理介绍

前面已经说过CART树利用基尼系数代替信息熵表示信息的不确定性，CART树实现分类的原理与ID3，C4.5一样，分别计算各个属性对降低基尼系数高低作为构建决策树结点的依据，与ID3，C4.5不同的是CART树是一个二叉树，对结点分裂时会选择一个切分点将一个属性的值分成两类计算，分成两类的过程代表二叉树子树的两个分支。

    CART树实现分类过程中每选择一个属性计算条件基尼系数时，都需要遍历整个属性值找到最佳切分点，然后再类似重复计算其他属性的条件基尼系数，择其最优的作为决策树结点，可以看到这个计算量比起ID3，C4.5是成倍上升的，所以CART树选择一个成本较低的二次函数而不是对数作为数学模型。综上所述，每个属性寻找最佳切分点是CART树与ID3，C4.5最大不同之处。

    另外需要注意的是，前面在提到C4.5对ID3改进时其中有一点是ID3偏好值是多元化的属性优先作为决策树结点，C4.5通过除以属性的信息熵来抵消了这方面的偏好，而CART树的条件基尼系数、基尼系数增益其形式都与为ID3的条件熵、信息增益一样，为什么这里就不存在ID3问题呢？或者说CART树是否偏好多元化的属性？其实仔细看一下CART树计算过程可以看到，由于切分点概念的引入，不管属性值有多少，都将所有属性值都划分成两部分，也就是说CART树认为所有的属性值只有两种情况，没有哪个属性能占到多样化这种便宜。

    下面看一个具体的CART树实现分类的例子，这是一个根据是否有房、婚姻状况、收入情况判断是否会拖欠贷款的分类过程，可以看到收入情况是一个数值型的属性，其他两个是离散型属性。

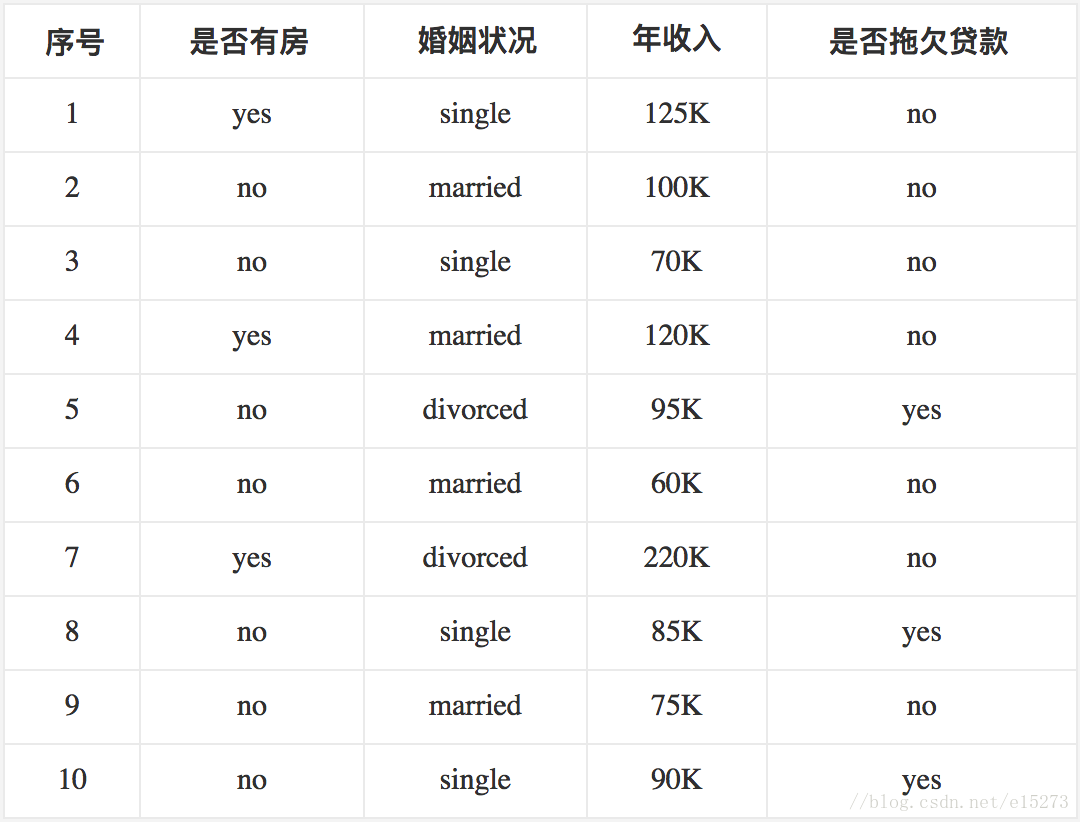
首先计算分类的基尼系数，这里拖欠贷款的有3例，不拖欠的有7例，利用公式(1)可得：

Gini(是否拖欠贷款)=1−(3/10)^2−(7/10)^2=0.42

然后分别计算属性的条件基尼系数，比如是否有房这个属性，由于这个属性本身只有两个分类，所以切分点只要一个即可：

 

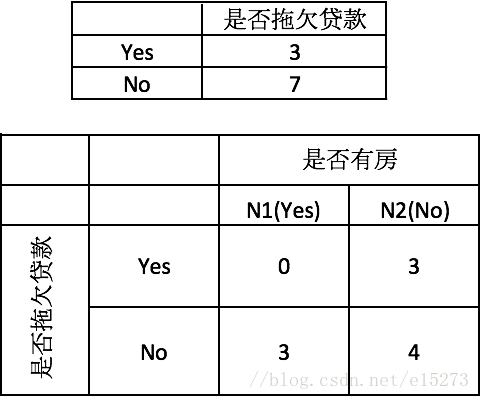
Gini(有房)=1−(0/3)^2−(3/3)^2=0

Gini(无房)=1−(3/7)^2−(4/7)^2=0.4898

Gain_Gini{是否拖欠贷款,是否有房}=0.42−7/10×0.4898−3/10×0=0.077

接下来看婚姻状况，该属性值有三个married，single，divorced，可先选{married} | {single,divorced}计算基尼系数增益为：

Gain_Gini{是否拖欠贷款,{married} | {single,divorced}}=0.42−4/10×0−6/10×[1−(3/6)^2−(3/6)^2]=0.12

移动切分点得到其他两种情况的基尼系数增益：

 

Gain_Gini{是否拖欠贷款,{single} | {married,divorced}}=0.42−4/10×0.5−6/10×[1−(1/6^)2−(5/6)^2]=0.053

Gain_Gini{是否拖欠贷款,{divorced} | {single,married}}=0.42−2/10×0.5−8/10×[1−(2/8)^2−(6/8)^2]=0.02

可以发现婚姻状况按{married} | {single,divorced}切分时基尼系数增益最大(条件基尼系数最小)，所以选择这个切分下计算出的基尼系数增益作为婚姻状况对是否拖欠贷款的基尼系数增益。

接下来看收入状况，收入是一个数值型属性，将属性值按从小到大排列,并将排列好的属性值两两计算平均值得到相邻中值点：

选择相邻中值点作为切分点，从小到大顺序先选择65K，小于65K的年收入为60K的为一个部分，大于65K是第二个部分，然后统计每个部分样本个数，利用上面的公式即可计算出基尼系数增益，从上图可以看到不同切分点下系数增益最大值是0.12，与婚姻状况的系数增益一样。

    以上计算完成了算法的第一步，接下来根据第二步选择婚姻状况作为决策树的节点，并选择切分点{married} | {single,divorced}作为二叉树的两个分支，将married作为左枝，{single,divorced}作为右枝，其中左枝有4个样本其类别都是no，这时左枝为叶结点不需要再分类；而右枝有6个样本，用余下的收入和是否有房两个属性再进行分类，此时剩下的6个样本数据的类别的基尼系数为：

Gini(是否拖欠贷款)=1−(3/6)^2−(3/6)^2=0.5

按是否有房对这6个样本计算系数增益可得：

Gain_Gini{是否拖欠贷款,是否有房}=0.5−4/6×[1−(3/4)^2−(1/4)^2]−2/6×0=0.25

收入情况系数增益表如下图:

最后得到CART树分类图如下所示:

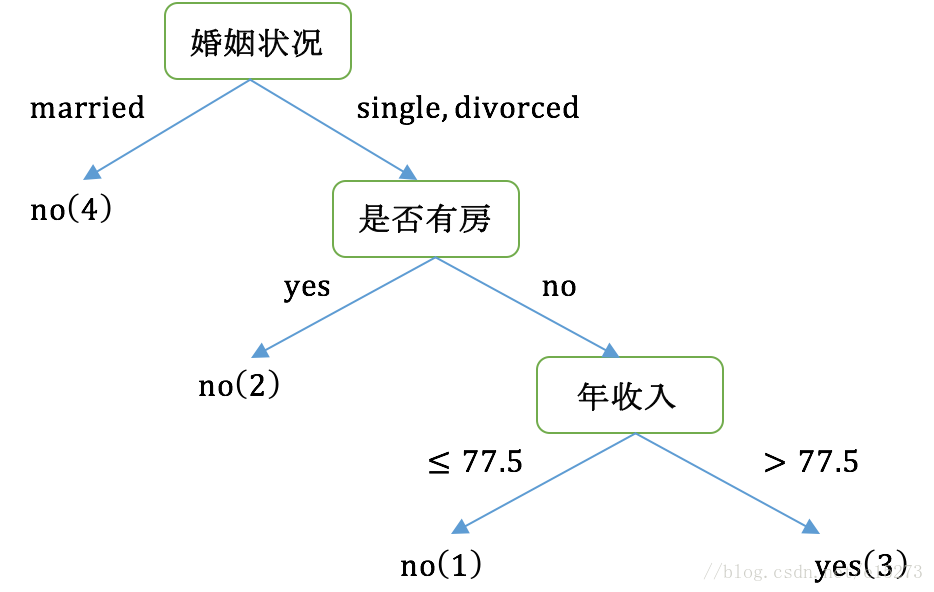
2.2 python实现CART分类与剪枝

    介绍C4.5时说过不剪枝的决策树是过拟合的，回顾C4.5剪枝算法是引入惩罚因子后，利用子树结点与叶结点之间的误差率，当两者误差率差不多时剪枝子树结点用叶结点代替从而降低过拟合，当时这个惩罚因子是一个固定的常数0.5，CART树剪枝算法与C4.5大致相同，只不过CART树剪枝算法的惩罚因子不再是一个固定的常数，观察下图，有内部结点t以及以t为根结点的子树Tt:

 

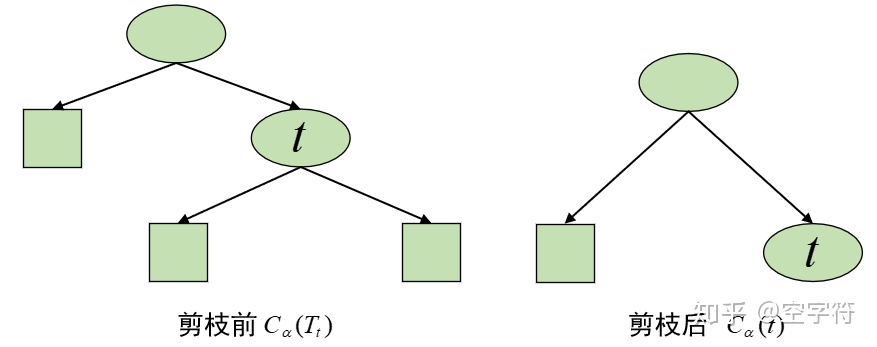
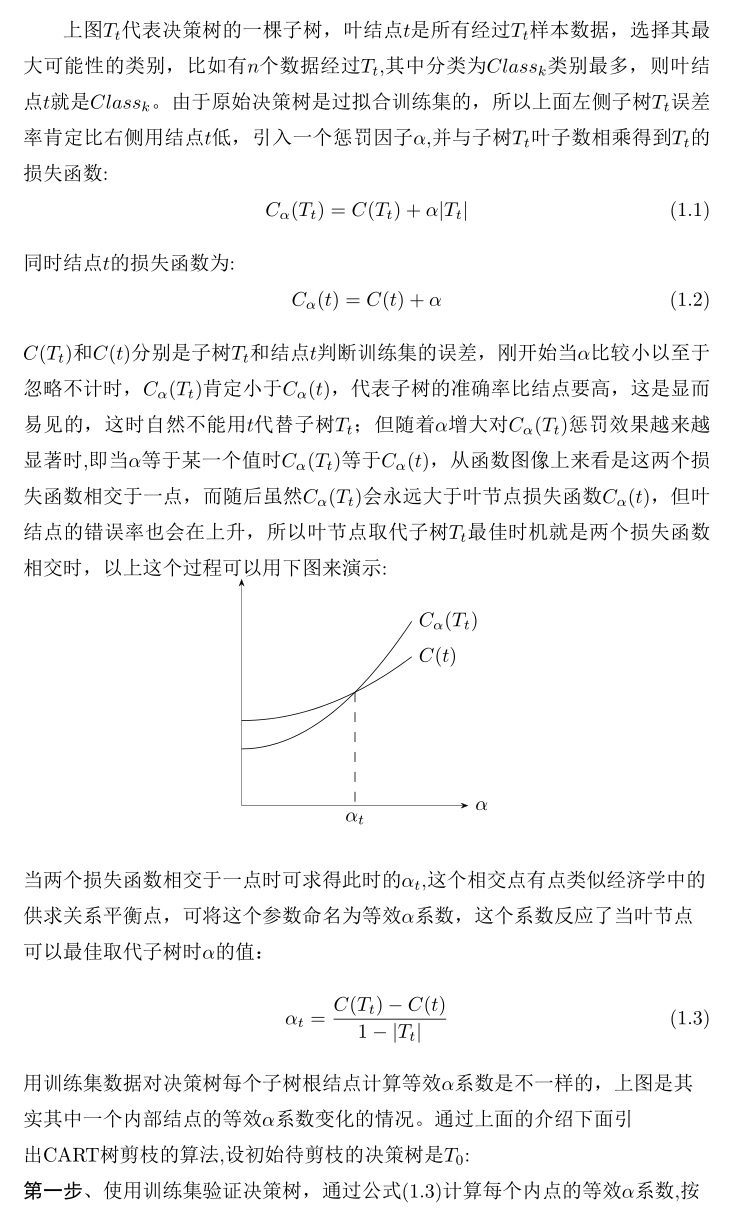
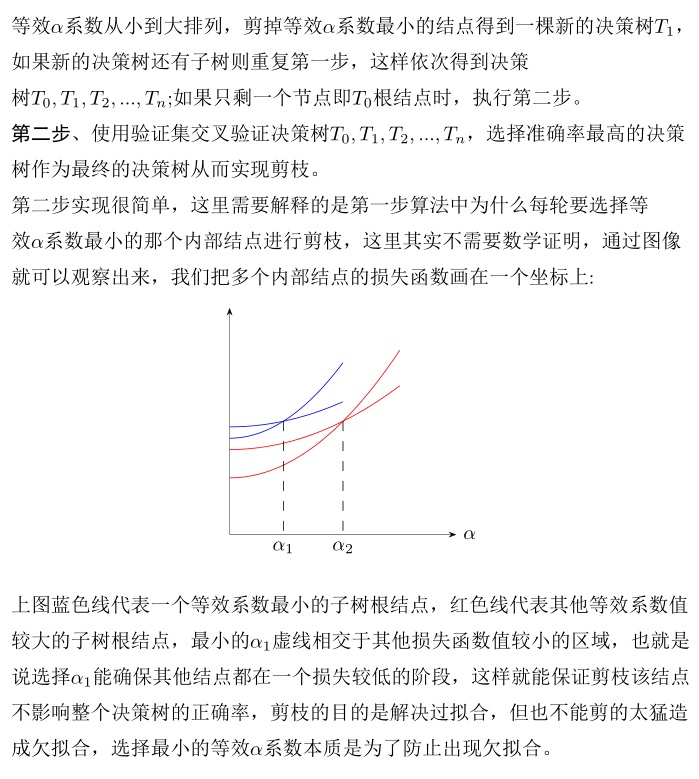
下面python代码实现CART树分类以及剪枝，样本数据是一些二手车数据，属性分别是：'购买时价格','后期保养','车门','装载人数','后备箱大小','安全性'，样本分类是根据以上特性得出的客户购买意向，主要有以下几类，acc：接受,unacc：不接受,good：好评,vgood:非常好。可以看出属性都是离散型的，所以这里用基尼系数来实现损失函数。

 

python实现cart树剪枝代码