ID3、C4.5与CART树的联系与区别：

参考博客：
链接1
链接2

特征选择准则：

ID3的特征选择准则为信息增益，即集合D的经验熵H(D)与给定特征A下条件经验熵H(D|A)之差，即：

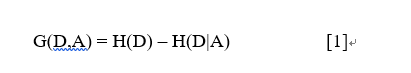
H(D)表现了数据集D进行分类的不确定性，而H(D|A)表现在特征A而使得对数据集D的分类的不确定性的减少。

有公式[1]可知，当特征取值较多时，H(D) – H(D|A)的差就越大，ID3决策树会偏向于选择取值较多的特征。

C4.5的特征选择准则为信息增益比，即：

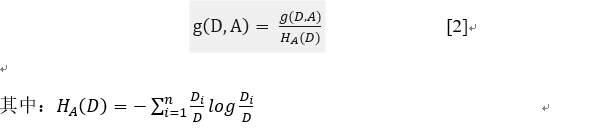
H_A(D)为数据集D关于特征A的值的熵，在信息增益比公式中充当了一个惩罚因子，迫使决策树不去选择特征取值过多的属性。这是C4.5对ID3改进的一点。

CART决策树在分类任务上选择基尼系数作为特征选择准则，其公式如下：

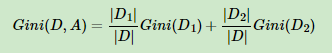
基尼系数的含义为：描述集合D的不确定性，基尼系数越大，也就是说集合的不确定性也越大。在二分类任务中，基尼系数与熵之半曲线很接近，都可以近似的表示分类误差率，因此可以使用基尼系数来作为分类任务的准则。

缺省值处理：

ID3算法：
对于缺失值的情况没有考虑
C4.5算法：

CART算法：
仍在挖坑………

连续特征处理：

ID3算法:
不能直接出来连续型特征,只能事先将连续型特征转为离散型，才能在ID3中使用。但这种转换过程会破坏连续型变量的内在性质。故使用二元切分法，具体的处理方法是: 如果特征值大于给定值就走左子树，否则走右子树。另外二元切分法也节省了树的构建时间。

C4.5算法：
采用的相邻数值平均值离散化的方式，这样就会具有多个切分点。

CART算法：
本身就可以处理连续型数值。

算法优缺点：

ID3算法优缺点：
（1）不能对连续数据进行处理，只能通过连续数据离散化进行处理；
（2）采用信息增益进行数据分裂容易偏向取值较多的特征，准确性不如信息增益率；
（3）缺失值不好处理。
（4）没有采用剪枝，决策树的结构可能过于复杂，出现过拟合。

C4.5算法优缺点：
(1) 产生的规则易于理解；准确率较高；实现简单；
(2) 对数据进行多次顺序扫描和排序，效率较低；
(3) 只适合小规模数据集，需要将数据放到内存中

CART算法优缺点：
(1) 无论是ID3， C4.5还是CART，在做特征选择的时候都是选择最优的一个特征来做分类决策，但是大多数，分类决策不应该是由某一个特征决定的，而是应该由一组特征决定的。这样决策得到的决策树更加准确。这个决策树叫做多变量决策树(multi-variate decision tree)。在选择最优特征的时候，多变量决策树不是选择某一个最优特征，而是选择最优的一个特征线性组合来做决策。

(2) 如果样本发生一点点的改动，就会导致树结构的剧烈改变。这个可以通过集成学习里面的随机森林之类的方法解决