---

🌠 『精品学习专栏导航帖』

• 🐳最适合入门的100个深度学习实战项目🐳
• 🐙【PyTorch深度学习项目实战100例目录】项目详解 + 数据集 + 完整源码🐙
• 🐶【机器学习入门项目10例目录】项目详解 + 数据集 + 完整源码🐶
• 🦜【机器学习项目实战10例目录】项目详解 + 数据集 + 完整源码🦜
• 🐌Java经典编程100例🐌
• 🦋Python经典编程100例🦋
• 🦄蓝桥杯历届真题题目+解析+代码+答案🦄
• 🐯【2023王道数据结构目录】课后算法设计题C、C++代码实现完整版大全🐯

---

---

2021人工智能领域新星创作者，带你从入门到精通，该博客每天更新，逐渐完善机器学习各个知识体系的文章，帮助大家更高效学习。

---

一、概述

针对于ID3和C4.5只能处理分类的问题，后来有人提出了CART，该模型是由Breima等人在1984年提出的，它是被应用广泛的决策树学习方法，它可以用于分类与回归问题，同样CART也是由特征选择、树的生成以及剪枝组成。

所以针对于该算法可以分为几种情况：

数据：离散型特征、连续型特征

标签：离散值、连续值

针对于不同的场景处理方式也大不相同，一般情况下选择特征划分节点时，如果标签为离散的，我们可以使用基尼系数作为划分标准，在ID3和C4.5中是使用信息增益方式进行评估，在CART中是使用基尼系数，如果标签是连续性的，显然不能够使用基尼系数，因为此时无法计算每个节点不同类别的概率，应使用均方误差来进行评估，原来是使用每个节点的熵值期望与原来的熵做差，如果标签连续使用均方误差，每个节点的均方误差与分割前节点的均方误差做对比。

二、CART决策树

1.分类树

其实CART分类树和ID3和C4.5的树生成算法差不多，只不过是在特征选择是采用了基尼系数

1.1 基尼系数

基尼系数公式的定义如下：
$$Gini(p)=\sum _{i=k}^K{p}_k(1-p_k)=1-\sum _{k=1}^K{p}_k^2$$

$$Gini(D)=1-\sum _{k=1}^K(\frac{|C_k|}{|D|}{)}^2$$

• K：样本的类别个数
• $p_k$ ：每个类别的概率
• $C_k$ ：每个类别的样本数
• D：样本总数

所以我们需要计算根据一个特征分割后的基尼系数与分割前的基尼系数做差：

假设A特征有两个值，所以可以分成两个节点，那么分割后的基尼系数为：
$$\begin{gathered} Gini(D,A)=p_{1}Gini(D_1)+p_{2}Gini(D_2) \\ =\frac{|D_1|}{|D|}Gini(D_1)+\frac{|D_2|}{|D|}Gini(D_2) \end{gathered}$$
我们也需要获得增益：
$$Gini(D,A)-Gini(D)$$
其实这个和熵非常相似，只不过是换个衡量指标罢了。

1.1 特征离散

如果特征是离散的，那么它就是按照特征的可选值进行划分节点，该特征有几个离散值，那么就划分成几个节点，和ID3、C4.5决策树一样。

1.2 特征连续

如果特征值是连续的，划分节点时就不能够按照特征的可选数量进行分割节点，因为连续特征有很多可选值，所以肯定不能和离散特征一样的分割方式，它是采用二叉树的方式，每次按照连续特征分成两个分支，分割方式为将待分割特征的所有值从小到大排序，然后选中其中一个值作为划分点，将样本划分为两个部分。

比如说，有一列特征A，值为 $[1,5,2,6,8,3]$​ ，按照顺序进行排序，$[1,2,3,5,6,8]$​ ，所以可选的值很多，我们假设选中3作为划分点，将原始样本划分为：$[1,2,3]$​ 和 $[5,6,8]$​ 。

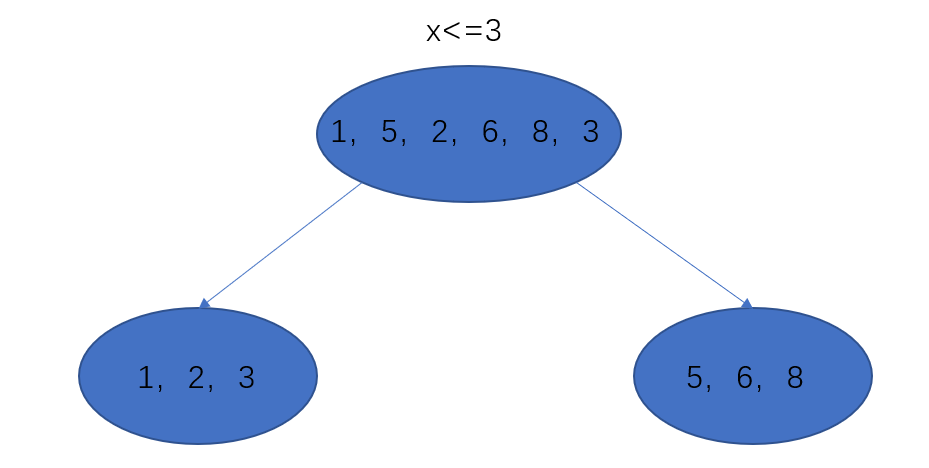
按照连续型特征分割后然后在用基尼系数进行评估。

2.回归树

其实回归树就是标签为连续型的，所以此时不能够使用基尼系数、熵这种的概率评估作为评估指标，因为不是分类不能够利用古典概型求出概率，所以我们考虑使用均方误差作为特征划分的好坏，将划分后的每个节点所有样本的均方误差之和之前没划分的节点的均方误差做差来代替基尼系数。

之前分类问题是计算所有特征的信息增益，此时我们会计算每个特征按照每个划分点的均方误差：
$$mi{n}_{j,s}[mi{n}_{c_1}\sum _{xi\in R_1(j,s)}(y_i-c1{)}^2+mi{n}_{c_2}\sum _{xi\in R_2(j,s)}(y_i-c2{)}^2]$$
上面的j是不同的特征，s是对应每个特征可供选择的划分点，因为一个连续特征的值很多，所以划分点很多，要选择最优的。

中括号内的意思就是找出针对特征j的最优划分点s，采用均方误差，最外层是特征，计算不同特征。

回归的比分类相对麻烦一些，分类只需要计算每个特征的信息增益，回归是计算每个特征的均方误差增益，但是它多了一个步骤就是求每个特征增益的时候还要找出最优划分值s。

这样生成的树成为最小二乘回归树。

算法流程：

1. 选择最优切分特征j和切分点s

$$mi{n}_{j,s}[mi{n}_{c_1}\sum _{xi\in R_1(j,s)}(y_i-c1{)}^2+mi{n}_{c_2}\sum _{xi\in R_2(j,s)}(y_i-c2{)}^2]$$

2. 用选定的对（j，s）划分区域并决定相应的输出值：

R 1 ( j , s ) = { x ∣ x ( j ) ≤ s } R 2 ( j , s ) = { x ∣ x ( j ) > s } R_1(j,s)=\{x|x^{(j)}\leq s\}\quad R_2(j,s)=\{x|x^{(j)}> s\} R1​(j,s)={x∣x(j)≤s}R2​(j,s)={x∣x(j)>s}

$$c_m=\frac{1}{N_m}\sum _{x_i\in R_m(j,s)}{y}_{i}x\in R_m,m=1,2$$

第一个式子是将数据按照切分点分成两个节点，第二个是求每个节点的均方误差之和。

3. 继续对两个子区域调用步骤1，2直至满足停止条件
4. 将输入空间划分为M个区域， $R_1,R_2,...R_M$ ，生成决策树：

$$f(x)=\sum _{i=1}^M{c}_{m}I(x\in R_m)$$

该式子的意思是求分到相同节点的均值作为预测值，后面的指示函数作为划分到那么区域。

三、剪枝算法

同样针对于CART决策树也存在防止过拟合的方法剪枝，CART剪枝算法由两步组成，首先从生成算法产生的决策树 $T_0$ 底端开始不断剪枝，直到 $T_0$ 的根节点，形成一个子树序列 { T 0 , T 1 , . . . , T n } \{T_0,T_1,...,T_n\} {T0​,T1​,...,Tn​} ，然后通过交叉验证法在独立的验证数据集熵对于子树序列进行测试，从中选择最优子树。

我们定义树模型的损失函数为：
$$C_a(T)=C(T)+a|T|$$
其中 $C(T)$ 为模型的预测误差（基尼系数、熵信息增益等），$a|T|$ 代表模型的复杂度，其中 $|T|$ 代表模型叶节点的个数，所以 $C_a(T)$ 可以作为树的整体损失，参数 a用于权衡训练数据的拟合程度与模型的复杂度。

取两个极端情况，如果a=0，那么此时的树是最茂盛的，如果a趋于无穷大，那么此时的树就为一个根节点，所以随着a的增大，我们的树会不断变小。

首先对 $T_0$​ 的任意内部节点t，以t为单节点树的损失函数为：
$$C_a(t)=C(t)+a$$
因为此时只有一个叶子节点。

以t为根节点的子树 $T_t$ 的损失函数为：
$$C_a(T_t)=C(T_t)+a|T_t|$$
当a=0时，有：
$$C_a(T_t)<C_a(t)$$
因为此时此时过拟合，很显然可以看出，当a增大时，存在a使得：
$$C_a(T_t)=C_a(t)$$
此时我们认为t节点和以该节点为根节点的子树损失值相同，损失同等情况下，我们选择复杂度小的t，所以进行剪枝，将t作为叶子节点。

此时的a为：
$$g(t)=a=\frac{C(t)-C(T_t)}{|T_t|-1}$$
在 $T_0$ 中减去 $g(t)$ 最小的 $T(t)$ ，将得到的子树作为 $T_1$ ，同时将最小的 $g(t)$ 设为 $a_1$ ，如此剪枝下去，直至得到根节点，然后利用独立的验证数据集取交叉验证获得的子树序列 $T_0,T_1,...T_n$ 获得最优决策树 $T_a$ ，其中每个决策子树对应一个 a。

写在最后

        大家好，我是阿光，觉得文章还不错的话，记得“一键三连”哦！！！