CART树算法解析加举例

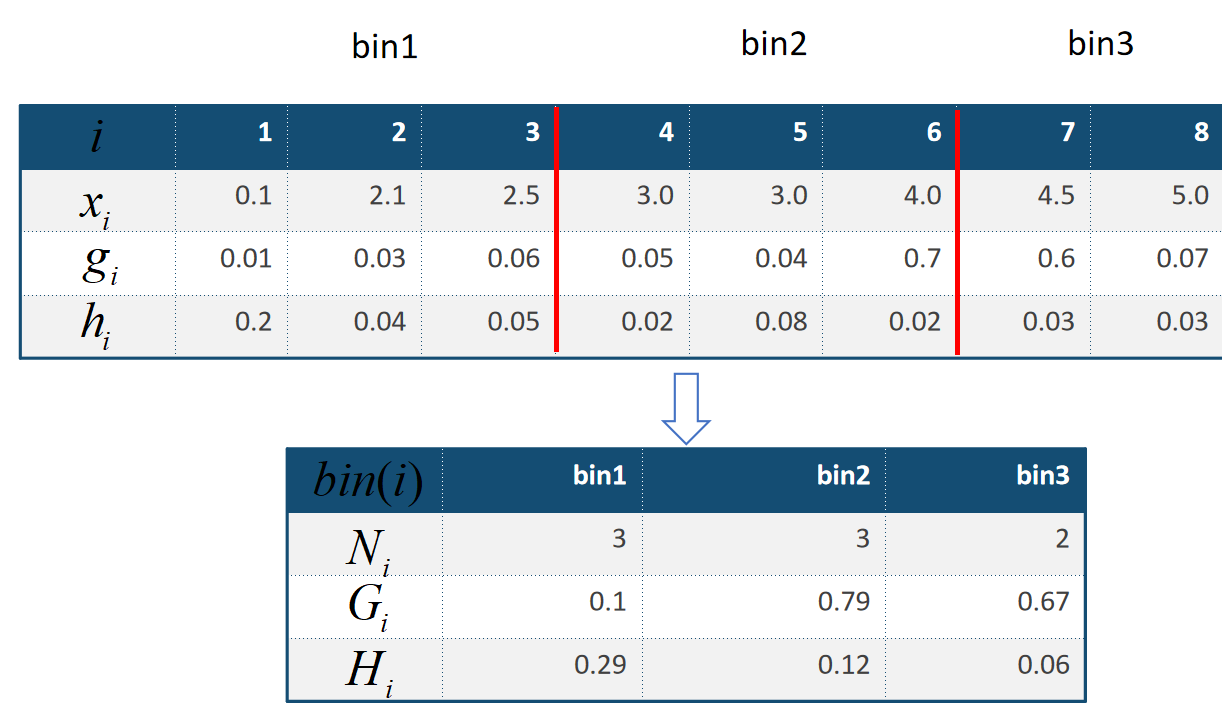
算法步骤

CART假设决策树是二叉树，内部结点特征的取值为“是”和“否”，左分支是取值为“是”的分支，右分支是取值为“否”的分支。这样的决策树等价于递归地二分每个特征，将输入空间即特征空间划分为有限个单元，并在这些单元上确定预测的概率分布，也就是在输入给定的条件下输出的条件概率分布。

CART算法由以下两步组成：

决策树生成：基于训练数据集生成决策树，生成的决策树要尽量大；
决策树剪枝：用验证数据集对已生成的树进行剪枝并选择最优子树，这时损失函数最小作为剪枝的标准。
CART决策树的生成就是递归地构建二叉决策树的过程。CART决策树既可以用于分类也可以用于回归。本文我们仅讨论用于分类的CART。对分类树而言，CART用Gini系数最小化准则来进行特征选择，生成二叉树。 CART生成算法如下：

输入：训练数据集D，停止计算的条件：
输出：CART决策树。

根据训练数据集，从根结点开始，递归地对每个结点进行以下操作，构建二叉决策树：

设结点的训练数据集为D，计算现有特征对该数据集的Gini系数。此时，对每一个特征A，对其可能取的每个值a，根据样本点对A=a的测试为“是”或 “否”将D分割成D1和D2两部分，计算A=a时的Gini系数。
在所有可能的特征A以及它们所有可能的切分点a中，选择Gini系数最小的特征及其对应的切分点作为最优特征与最优切分点。依最优特征与最优切分点，从现结点生成两个子结点，将训练数据集依特征分配到两个子结点中去。
对两个子结点递归地调用步骤l~2，直至满足停止条件。
生成CART决策树。
算法停止计算的条件是结点中的样本个数小于预定阈值，或样本集的Gini系数小于预定阈值（样本基本属于同一类），或者没有更多特征。

Gini指数的计算

其实gini指数最早应用在经济学中，主要用来衡量收入分配公平度的指标。在决策树算CART算法中用gini指数来衡量数据的不纯度或者不确定性，同时用gini指数来决定类别变量的最优二分值得切分问题。

在分类问题中，假设有K个类，样本点属于第k类的概率为Pk，则概率分布的gini指数的定义为：
这里写图片描述

如果样本集合D根据某个特征A被分割为D1，D2两个部分，那么在特征A的条件下，集合D的gini指数的定义为：
这里写图片描述
gini指数Gini(D,A)表示特征A不同分组的数据集D的不确定性。gini指数值越大，样本集合的不确定性也就越大，这一点与熵的概念比较类似。

所以在此，基于以上的理论，我们可以通过gini指数来确定某个特征的最优切分点(也即只需要确保切分后某点的gini指数值最小)，这就是决策树CART算法中类别变量切分的关键所在。是不是对于决策树的CART算法有点小理解啦！其实，这里可以进一步拓展到我们对于类别变量的粗分类应用上来。比如我某个特征变量下有20多个分组，现在我只想要5个大类，如何将这个20多个类合并为5个大类，如何分类最优，以及如何找到最优的分类。这些建模初期的数据预处理问题其实我们都可以用gini指数来解决。

例子

这里写图片描述

首先对数据集非类标号属性{是否有房，婚姻状况，年收入}分别计算它们的Gini系数增益，取Gini系数增益值最大的属性作为决策树的根节点属性。根节点的Gini系数

Gini(是否拖欠贷款)=1−(3/10)^2−(7/10)^2=0.42

当根据是否有房来进行划分时，Gini系数增益计算过程为

这里写图片描述

Gini(左子节点)=1−(0/3)^2−(3/3)^2=0

Gini(右子节点)=1−(3/7)^2−(4/7)^2=0.4898

Δ{是否有房}=0.42−710×0.4898−310×0=0.077

若按婚姻状况属性来划分，属性婚姻状况有三个可能的取值{married，single，divorced}，分别计算划分后的

{married} | {single,divorced}
{single} | {married,divorced}
{divorced} | {single,married}

的Gini系数增益。
当分组为{married} | {single,divorced}时，Sl表示婚姻状况取值为married的分组，Sr表示婚姻状况取值为single或者divorced的分组

Δ{婚姻状况}=0.42−4/10×0−6/10×[1−(3/6)^2−(3/6)^2]=0.12

当分组为{single} | {married,divorced}时，
Δ{婚姻状况}=0.42−4/10×0.5−6/10×[1−(1/6^)2−(5/6)^2]=0.053

当分组为{divorced} | {single,married}时，
Δ{婚姻状况}=0.42−2/10×0.5−8/10×[1−(2/8)^2−(6/8)^2]=0.02

对比计算结果，根据婚姻状况属性来划分根节点时取Gini系数增益最大的分组作为划分结果，也就是{married} | {single,divorced}。
最后考虑年收入属性，我们发现它是一个连续的数值类型。我们在前面的文章里已经专门介绍过如何应对这种类型的数据划分了。对此还不是很清楚的朋友可以参考之前的文章，这里不再赘述。

对于年收入属性为数值型属性，首先需要对数据按升序排序，然后从小到大依次用相邻值的中间值作为分隔将样本划分为两组。例如当面对年收入为60和70这两个值时，我们算得其中间值为65。倘若以中间值65作为分割点。Sl作为年收入小于65的样本，Sr表示年收入大于等于65的样本，于是则得Gini系数增益为

Δ(年收入)=0.42−1/10×0−9/10×[1−(6/9)^2−(3/9)^2]=0.02

其他值的计算同理可得，我们不再逐一给出计算过程，仅列出结果如下（最终我们取其中使得增益最大化的那个二分准则来作为构建二叉树的准则）：
这里写图片描述

注意，这与我们之前在《数据挖掘十大算法之决策树详解（1）》中得到的结果是一致的。最大化增益等价于最小化子女结点的不纯性度量（Gini系数）的加权平均值，之前的表里我们列出的是Gini系数的加权平均值，现在的表里给出的是Gini系数增益。现在我们希望最大化Gini系数的增益。根据计算知道，三个属性划分根节点的增益最大的有两个：年收入属性和婚姻状况，他们的增益都为0.12。此时，选取首先出现的属性作为第一次划分。

接下来，采用同样的方法，分别计算剩下属性，其中根节点的Gini系数为（此时是否拖欠贷款的各有3个records）
Gini(是否拖欠贷款)=1−(3/6)^2−(3/6)^2=0.5

与前面的计算过程类似，对于是否有房属性，可得
Δ{是否有房}=0.5−4/6×[1−(3/4)^2−(1/4)^2]−2/6×0=0.25

对于年收入属性则有：
这里写图片描述

最后我们构建的CART如下图所示：
这里写图片描述

最后我们总结一下，CART和C4.5的主要区别：

C4.5采用信息增益率来作为分支特征的选择标准，而CART则采用Gini系数；
C4.5不一定是二叉树，但CART一定是二叉树。

关于过拟合以及剪枝

决策树很容易发生过拟合，也就是由于对train数据集适应得太好，反而在test数据集上表现得不好。这个时候我们要么是通过阈值控制终止条件避免树形结构分支过细，要么就是通过对已经形成的决策树进行剪枝来避免过拟合。另外一个克服过拟合的手段就是基于Bootstrap的思想建立随机森林（Random Forest）。关于剪枝的内容可以参考文献【2】以了解更多，如果有机会我也可能在后续的文章里讨论它。

参考文献

【1】Wu, X., Kumar, V., Quinlan, J.R., Ghosh, J., Yang, Q., Motoda, H., McLachlan, G.J., Ng, A., Liu, B., Philip, S.Y. and Zhou, Z.H., 2008. Top 10 algorithms in data mining. Knowledge and information systems, 14(1), pp.1-37. (http://www.cs.uvm.edu/~icdm/algorithms/10Algorithms-08.pdf）
【2】李航，统计学习方法，清华大学出版社