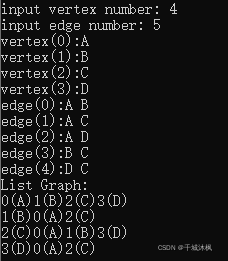
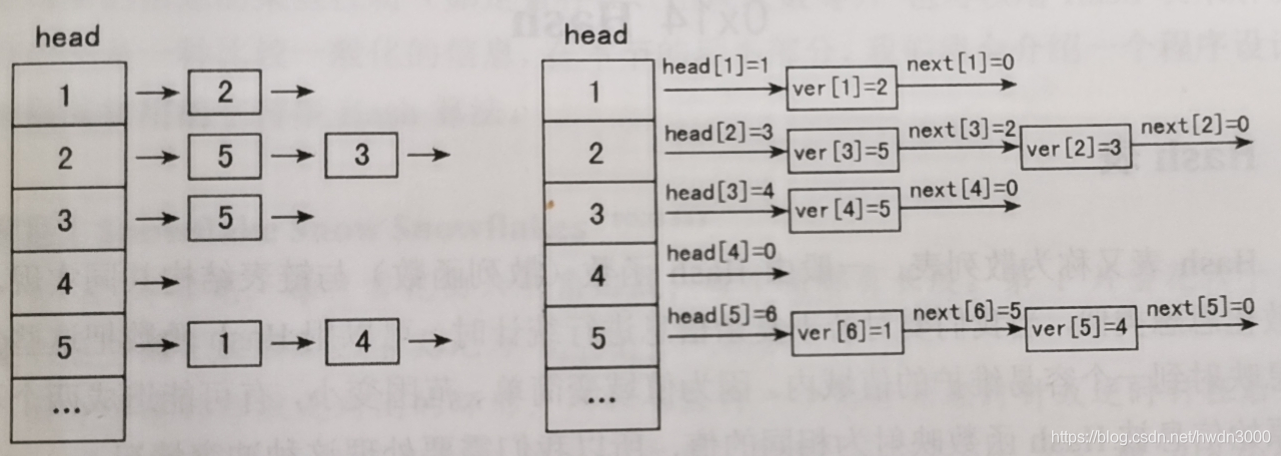
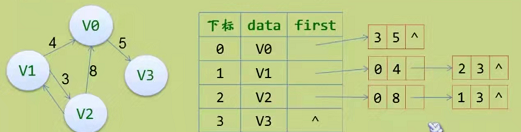
邻接表表示法(链式)

存储定义：

• 顶点：按编号顺序将顶点数据存储在一维数组中
• 关联同一顶点的边(以顶点为尾的弧)：用线性链表存储

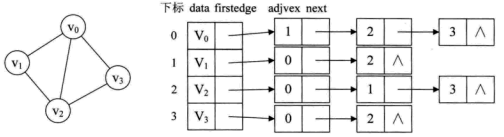
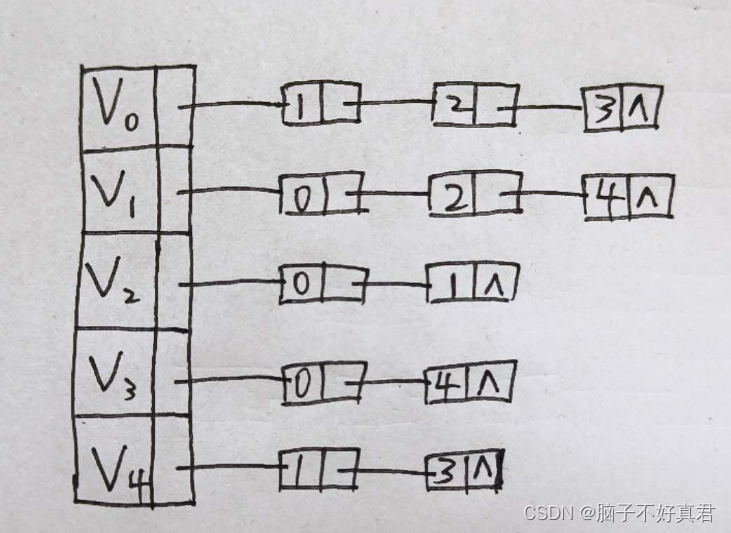
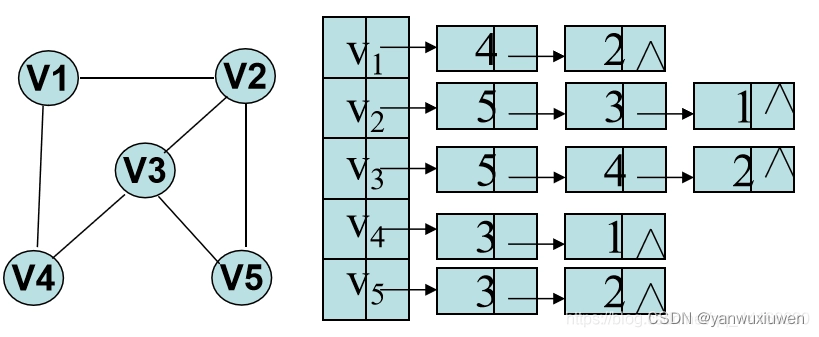
无向图的邻接表

例如，如下无向图

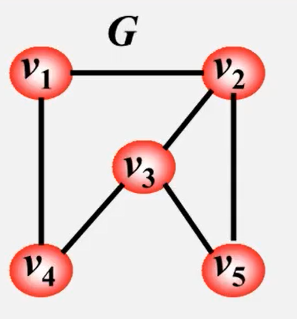
则它的邻接表为

无向图邻接表的特点：

• 邻接表不唯一
• 若无向图中有 n 个顶点，e 条边，则其邻接表需要 n 个头结点和 2e 个表节点，适宜存稀疏图。
• 无向图中顶点 Vi 的度为第 i 个单链表中的节点数。
• 存储空间 n + 2e

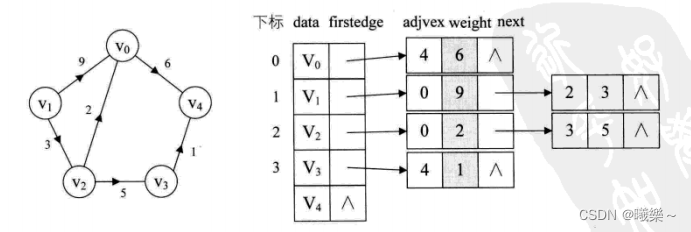
有向图的邻接表

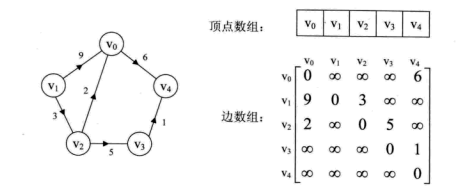
如下有向图

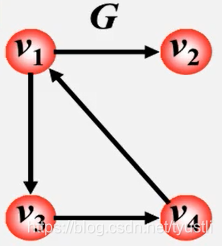
则它的邻接矩阵为

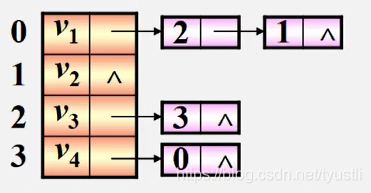
它的逆邻接矩阵为

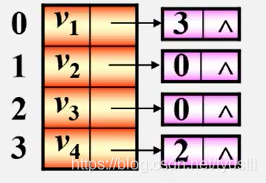
有向图邻接表的特点：

• 顶点 Vi 的出度为第 i 个单链表中结点个数
• 顶点 Vi 的入度为整个单链表中邻接点域值是 i - 1 的节点个数
• 找出度易，找入度难

有向图逆邻接表的特点：

• 顶点 Vi 的入度为第 i 个单链表中结点个数
• 顶点 Vi 的出度为整个单链表中邻接点域值是 i - 1 的节点个数
• 找入度易，找出度难

邻接表的特点

• 方便找任一顶点的所有邻接点
• 节约稀疏图的空间
  • 需要 N 个头指针 + 2E 个结点(每个结点至少2个域)
• 计算任一顶点的度
  • 无向图：方便
  • 有向图：只能计算 出度；需要构造 逆邻接表 来方便计算 入度
• 不方便检查任意一对顶点间是否存在边

邻接矩阵和邻接表的关系

联系：

• 邻接表中每个链表对应邻接矩阵中的一行，链表中结点个数等于一行中非零元素的个数

区别：

• 对于任意确定的无向图，邻接矩阵是唯一的(行列号与顶点编号一致)，但邻接表不唯一(链接次序与顶点编号无关)

• 邻接矩阵的空间复杂度为O(n²)，而邻接表的空间复杂度为 O(n+e)

用途：

• 邻接矩阵多用于稠密图；而邻接表多用于稀疏图。

邻接表的存储方式

typedef int InfoType;              // 网的权值类型
typedef char VertexType[MAX_NAME]; // 顶点类型为字符串enum GraphKind
{DG,DN,UDG,UDN
}; // {有向图,有向网,无向图,无向网}struct ElemType
{int adjvex;     // 该弧所指向的顶点的位置InfoType *info; // 网的权值指针
};struct ArcNode
{struct ElemType data;    // 除指针以外的部分都属于ElemTypestruct ArcNode *nextarc; // 指向下一条弧的指针
};                           // 表结点
typedef struct
{VertexType data;              // 顶点信息struct ArcNode *firstarc;     // 第一个表结点的地址,指向第一条依附该顶点的弧的指针
} VNode, AdjList[MAX_VERTEX_NUM]; // 头结点struct ALGraph
{AdjList vertices;int vexnum, arcnum;  // 图的当前顶点数和弧数enum GraphKind kind; // 图的种类标志
};

邻接表的代码实现

main.c

/** Change Logs:* Date           Author       Notes* 2021-08.03     tyustli      first version*/#include "graph.h"void visit(VertexType i)
{printf("%s ", i);
}int main(int argc, char *argv[])
{int i, j, k, n;struct ALGraph g;VertexType v1, v2;printf("请顺序选择有向图,有向网,无向图,无向网\n");printf("this is graph\r\n");CreateGraphF(&g);Display(g);DFSTraverse(g, visit);BFSTraverse(g, visit);return 1;
}
/*
编译：make
运行：./obj
结果：
请顺序选择有向图,有向网,无向图,无向网
this is graph
请输入数据文件名(f7-1.txt或f7-2.txt)：graph.txt
请输入图的类型(有向图:0,有向网:1,无向图:2,无向网:3): 2
无向图
8个顶点：
a b c d e f g h
14条弧(边):
a→h a→g a→f a→e a→c a→b
b→h b→e b→d
c→h c→g
d→h
e→f
f→ga h d b e f g c
a h g f e c b d
*/
/************************ end of file **************************/

makefile

objects  = main.o graph.o
obj: $(objects)cc -o obj $(objects) -lmmain.o : graph.h
graph.o : graph.h.PHONY : clean
clean :-rm obj $(objects)

graph.h

/** Change Logs:* Date           Author       Notes* 2021-08.03     tyustli      first version*/#include <string.h>
#include <ctype.h>
#include <malloc.h> // malloc()等
#include <limits.h> // INT_MAX等
#include <stdio.h>  // EOF(=^Z或F6),NULL
#include <stdlib.h> // atoi()// 函数结果状态代码
#define TRUE 1
#define FALSE 0
#define OK 1
#define ERROR 0
#define INFEASIBLE -1
#define OVERFLOW -2
typedef int Status;  // Status是函数的类型,其值是函数结果状态代码，如OK等
typedef int Boolean; // Boolean是布尔类型,其值是TRUE或FALSE#define MAX_VERTEX_NUM 20
#define MAX_NAME 3 // 顶点字符串的最大长度+1typedef int InfoType;              // 网的权值类型
typedef char VertexType[MAX_NAME]; // 顶点类型为字符串enum GraphKind
{DG,DN,UDG,UDN
}; // {有向图,有向网,无向图,无向网}struct ElemType
{int adjvex;     // 该弧所指向的顶点的位置InfoType *info; // 网的权值指针
};struct ArcNode
{struct ElemType data;    // 除指针以外的部分都属于ElemTypestruct ArcNode *nextarc; // 指向下一条弧的指针
};                           // 表结点
typedef struct
{VertexType data;              // 顶点信息struct ArcNode *firstarc;     // 第一个表结点的地址,指向第一条依附该顶点的弧的指针
} VNode, AdjList[MAX_VERTEX_NUM]; // 头结点struct ALGraph
{AdjList vertices;int vexnum, arcnum;  // 图的当前顶点数和弧数enum GraphKind kind; // 图的种类标志
};#define LNode struct ArcNode      // 定义单链表的结点类型是图的表结点的类型
#define next nextarc              // 定义单链表结点的指针域是表结点指向下一条弧的指针域
typedef struct ArcNode *LinkList; // 定义指向单链表结点的指针是指向图的表结点的指针void CreateGraph(struct ALGraph *G);
void CreateGraphF(struct ALGraph *G);
void Display(struct ALGraph G);
void DFSTraverse(struct ALGraph G, void (*Visit)(char *));
void BFSTraverse(struct ALGraph G, void (*Visit)(char *));/************************ end of file **************************/

graph.c

/** Change Logs:* Date           Author       Notes* 2021-08.03     tyustli      first version*/#include "graph.h"#if 1
// 不带头结点的单链表的部分基本操作 邻接表中会用到链表的插入等操作
#define DestroyList ClearList // DestroyList()和ClearList()的操作是一样的
void InitList(LinkList *L)
{*L = NULL; // 指针为空
}
void ClearList(LinkList *L)
{ // 初始条件：线性表L已存在。操作结果：将L重置为空表LinkList p;while (*L) // L不空{p = *L;          // p指向首元结点*L = (*L)->next; // L指向第2个结点(新首元结点)free(p);         // 释放首元结点}
}
Status ListEmpty(LinkList L)
{ // 初始条件：线性表L已存在。操作结果：若L为空表，则返回TRUE，否则返回FALSEif (L)return FALSE;elsereturn TRUE;
}
int ListLength(LinkList L)
{ // 初始条件：线性表L已存在。操作结果：返回L中数据元素个数int i = 0;LinkList p = L;while (p) // p指向结点(没到表尾){p = p->next; // p指向下一个结点i++;}return i;
}
Status GetElem(LinkList L, int i, struct ElemType *e)
{int j = 1;LinkList p = L;if (i < 1) // i值不合法return ERROR;while (j < i && p) // 没到第i个元素，也没到表尾{j++;p = p->next;}if (j == i) // 存在第i个元素{*e = p->data;return OK;}elsereturn ERROR;
}
int LocateElem(LinkList L, struct ElemType e, Status (*compare)(struct ElemType, struct ElemType))
{int i = 0;LinkList p = L;while (p){i++;if (compare(p->data, e)) // 找到这样的数据元素return i;p = p->next;}return 0;
}Status ListInsert(LinkList *L, int i, struct ElemType e)
{ // 在不带头结点的单链线性表L中第i个位置之前插入元素eint j = 1;LinkList p = *L, s;if (i < 1) // i值不合法return ERROR;s = (LinkList)malloc(sizeof(LNode)); // 生成新结点s->data = e;                         // 给s的data域赋值if (i == 1)                          // 插在表头{s->next = *L;*L = s; // 改变L}else{                          // 插在表的其余处while (p && j < i - 1) // 寻找第i-1个结点{p = p->next;j++;}if (!p) // i大于表长+1return ERROR;s->next = p->next;p->next = s;}return OK;
}
Status ListDelete(LinkList *L, int i, struct ElemType *e)
{ // 在不带头结点的单链线性表L中，删除第i个元素，并由e返回其值int j = 1;LinkList p = *L, q;if (i == 1) // 删除第1个结点{*L = p->next; // L由第2个结点开始*e = p->data;free(p); // 删除并释放第1个结点}else{while (p->next && j < i - 1) // 寻找第i个结点，并令p指向其前趋{p = p->next;j++;}if (!p->next || j > i - 1) // 删除位置不合理return ERROR;q = p->next; // 删除并释放结点p->next = q->next;*e = q->data;free(q);}return OK;
}LinkList Point(LinkList L, struct ElemType e, Status (*equal)(struct ElemType, struct ElemType), LinkList *p)
{ // 查找表L中满足条件的结点。如找到，返回指向该结点的指针，p指向该结点的前驱(若该结点是// 首元结点，则p=NULL)。如表L中无满足条件的结点，则返回NULL，p无定义。// 函数equal()的两形参的关键字相等，返回OK；否则返回ERRORint i, j;i = LocateElem(L, e, equal);if (i) // 找到{if (i == 1) // 是首元结点{*p = NULL;return L;}*p = L;for (j = 2; j < i; j++)*p = (*p)->next;return (*p)->next;}return NULL; // 没找到
}Status DeleteElem(LinkList *L, struct ElemType *e, Status (*equal)(struct ElemType, struct ElemType))
{ // 删除表L中满足条件的结点，并返回TRUE；如无此结点，则返回FALSE。// 函数equal()的两形参的关键字相等，返回OK；否则返回ERRORLinkList p, q;q = Point(*L, *e, equal, &p);if (q) // 找到此结点，且q指向该结点{if (p)                    // 该结点不是首元结点，p指向其前驱ListDelete(&p, 2, e); // 将p作为头指针,删除第2个结点else                      // 该结点是首元结点ListDelete(L, 1, e);return TRUE;}return FALSE;
}void ListTraverse(LinkList L, void (*vi)(struct ElemType))
{ // 初始条件：线性表L已存在。操作结果：依次对L的每个数据元素调用函数vi()LinkList p = L;while (p){vi(p->data);p = p->next;}printf("\n");
}
#endif// 图的邻接表存储的基本操作// 初始条件：图 G 存在，u 和 G 中顶点有相同特征
// 操作结果：若 G 中存在顶点 u，则返回该顶点在图中位置；否则返回 -1
int LocateVex(struct ALGraph G, VertexType u)
{int i;for (i = 0; i < G.vexnum; ++i)if (strcmp(u, G.vertices[i].data) == 0)return i;return -1;
}// 采用邻接表存储结构，构造没有相关信息图或网G(用一个函数构造4种图)void CreateGraph(struct ALGraph *G)
{                      // 采用邻接表存储结构，构造没有相关信息图或网G(用一个函数构造4种图)int i, j, k, w;    // w是权值VertexType va, vb; // 连接边或弧的2顶点struct ElemType e;printf("请输入图的类型(有向图:0,有向网:1,无向图:2,无向网:3): ");scanf("%d", (int *)&G->kind);printf("请输入图的顶点数,边数: ");scanf("%d,%d", &G->vexnum, &G->arcnum);printf("请输入%d个顶点的值(<%d个字符):\n", G->vexnum, MAX_NAME);for (i = 0; i < G->vexnum; ++i) // 构造顶点向量{scanf("%s", G->vertices[i].data);G->vertices[i].firstarc = NULL; // 初始化与该顶点有关的出弧链表}if (G->kind % 2) // 网printf("请输入每条弧(边)的权值、弧尾和弧头(以空格作为间隔):\n");else // 图printf("请输入每条弧(边)的弧尾和弧头(以空格作为间隔):\n");for (k = 0; k < G->arcnum; ++k) // 构造相关弧链表{if (G->kind % 2) // 网scanf("%d%s%s", &w, va, vb);else // 图scanf("%s%s", va, vb);i = LocateVex(*G, va); // 弧尾j = LocateVex(*G, vb); // 弧头e.info = NULL;         // 给待插表结点e赋值，图无权e.adjvex = j;          // 弧头if (G->kind % 2)       // 网{e.info = (int *)malloc(sizeof(int)); // 动态生成存放权值的空间*(e.info) = w;}ListInsert(&G->vertices[i].firstarc, 1, e); // 插在第i个元素(出弧)的表头，在bo2-8.cpp中if (G->kind >= 2)                           // 无向图或网，产生第2个表结点，并插在第j个元素(入弧)的表头{e.adjvex = i;                               // e.info不变，不必再赋值ListInsert(&G->vertices[j].firstarc, 1, e); // 插在第j个元素的表头，在bo2-8.cpp中}}
}// 采用邻接表存储结构，由文件构造没有相关信息图或网G(用一个函数构造4种图)
void CreateGraphF(struct ALGraph *G)
{int i, j, k, w;    // w是权值VertexType va, vb; // 连接边或弧的2顶点struct ElemType e;char filename[13];FILE *graphlist;printf("请输入数据文件名(f7-1.txt或f7-2.txt)：");scanf("%s", filename);printf("请输入图的类型(有向图:0,有向网:1,无向图:2,无向网:3): ");scanf("%d", (int *)&G->kind);graphlist = fopen(filename, "r"); // 以读的方式打开数据文件，并以graphlist表示fscanf(graphlist, "%d", &G->vexnum);fscanf(graphlist, "%d", &G->arcnum);for (i = 0; i < G->vexnum; ++i) // 构造顶点向量{fscanf(graphlist, "%s", G->vertices[i].data);G->vertices[i].firstarc = NULL; // 初始化与该顶点有关的出弧链表}for (k = 0; k < G->arcnum; ++k) // 构造相关弧链表{if (G->kind % 2) // 网fscanf(graphlist, "%d%s%s", &w, va, vb);else // 图fscanf(graphlist, "%s%s", va, vb);i = LocateVex(*G, va); // 弧尾j = LocateVex(*G, vb); // 弧头e.info = NULL;         // 给待插表结点e赋值，图无权e.adjvex = j;          // 弧头if (G->kind % 2)       // 网{e.info = (int *)malloc(sizeof(int)); // 动态生成存放权值的空间*(e.info) = w;}ListInsert(&G->vertices[i].firstarc, 1, e); // 插在第i个元素(出弧)的表头，在bo2-8.cpp中if (G->kind >= 2)                           // 无向图或网，产生第2个表结点，并插在第j个元素(入弧)的表头{e.adjvex = i;                               // e.info不变，不必再赋值ListInsert(&G->vertices[j].firstarc, 1, e); // 插在第j个元素的表头，在bo2-8.cpp中}}fclose(graphlist); // 关闭数据文件
}void DestroyGraph(struct ALGraph *G)
{ // 初始条件：图G存在。操作结果：销毁图Gint i;struct ElemType e;for (i = 0; i < G->vexnum; ++i)         // 对于所有顶点if (G->kind % 2)                    // 网while (G->vertices[i].firstarc) // 对应的弧或边链表不空{ListDelete(&G->vertices[i].firstarc, 1, &e); // 删除链表的第1个结点，并将值赋给eif (e.adjvex > i)                            // 顶点序号>i(保证动态生成的权值空间只释放1次)free(e.info);}else                                       // 图DestroyList(&G->vertices[i].firstarc); // 销毁弧或边链表，在bo2-8.cpp中G->vexnum = 0;                                 // 顶点数为0G->arcnum = 0;                                 // 边或弧数为0
}// 初始条件：图G存在，v是G中某个顶点的序号。操作结果：返回v的值
VertexType *GetVex(struct ALGraph G, int v)
{if (v >= G.vexnum || v < 0)exit(ERROR);return G.vertices[v].data;
}// 初始条件：图G存在，v是G中某个顶点。操作结果：对v赋新值value
Status PutVex(struct ALGraph *G, VertexType v, VertexType value)
{int i;i = LocateVex(*G, v);if (i > -1) // v是G的顶点{strcpy(G->vertices[i].data, value);return OK;}return ERROR;
}// 初始条件：图G存在，v是G中某个顶点
// 操作结果：返回v的第一个邻接顶点的序号。若顶点在G中没有邻接顶点，则返回-1
int FirstAdjVex(struct ALGraph G, VertexType v)
{struct ArcNode *p;int v1;v1 = LocateVex(G, v); // v1为顶点v在图G中的序号p = G.vertices[v1].firstarc;if (p)return p->data.adjvex;elsereturn -1;
}// DeleteArc()、DeleteVex()和NextAdjVex()要调用的函数
Status equalvex(struct ElemType a, struct ElemType b)
{if (a.adjvex == b.adjvex)return OK;elsereturn ERROR;
}// 初始条件：图G存在，v是G中某个顶点，w是v的邻接顶点
// 操作结果：返回v的(相对于w的)下一个邻接顶点的序号。若w是v的最后一个邻接点，则返回-1
int NextAdjVex(struct ALGraph G, VertexType v, VertexType w)
{LinkList p, p1; // p1在Point()中用作辅助指针，Point()在func2-1.cpp中struct ElemType e;int v1;v1 = LocateVex(G, v);                                 // v1为顶点v在图G中的序号e.adjvex = LocateVex(G, w);                           // e.adjvex为顶点w在图G中的序号p = Point(G.vertices[v1].firstarc, e, equalvex, &p1); // p指向顶点v的链表中邻接顶点为w的结点if (!p || !p->next)                                   // 没找到w或w是最后一个邻接点return -1;else                             // p->data.adjvex==wreturn p->next->data.adjvex; // 返回v的(相对于w的)下一个邻接顶点的序号
}// 初始条件：图G存在，v和图中顶点有相同特征
// 操作结果：在图G中增添新顶点v(不增添与顶点相关的弧，留待InsertArc()去做)
void InsertVex(struct ALGraph *G, VertexType v)
{strcpy(G->vertices[G->vexnum].data, v); // 构造新顶点向量G->vertices[G->vexnum].firstarc = NULL;G->vexnum++; // 图G的顶点数加1
}// 初始条件：图G存在，v是G中某个顶点。操作结果：删除G中顶点v及其相关的弧
Status DeleteVex(struct ALGraph *G, VertexType v)
{int i, j, k;struct ElemType e;LinkList p, p1;j = LocateVex(*G, v); // j是顶点v的序号if (j < 0)            // v不是图G的顶点return ERROR;i = ListLength(G->vertices[j].firstarc); // 以v为出度的弧或边数，在bo2-8.cpp中G->arcnum -= i;                          // 边或弧数-iif (G->kind % 2)                         // 网while (G->vertices[j].firstarc)      // 对应的弧或边链表不空{ListDelete(&G->vertices[j].firstarc, 1, &e); // 删除链表的第1个结点，并将值赋给efree(e.info);                                // 释放动态生成的权值空间}else                                       // 图DestroyList(&G->vertices[j].firstarc); // 销毁弧或边链表，在bo2-8.cpp中G->vexnum--;                               // 顶点数减1for (i = j; i < G->vexnum; i++)            // 顶点v后面的顶点前移G->vertices[i] = G->vertices[i + 1];for (i = 0; i < G->vexnum; i++) // 删除以v为入度的弧或边且必要时修改表结点的顶点位置值{e.adjvex = j;p = Point(G->vertices[i].firstarc, e, equalvex, &p1); // Point()在func2-1.cpp中if (p)                                                // 顶点i的邻接表上有v为入度的结点{if (p1)                                // p1指向p所指结点的前驱p1->next = p->next;                // 从链表中删除p所指结点else                                   // p指向首元结点G->vertices[i].firstarc = p->next; // 头指针指向下一结点if (G->kind < 2)                       // 有向{G->arcnum--;            // 边或弧数-1if (G->kind == 1)       // 有向网free(p->data.info); // 释放动态生成的权值空间}free(p); // 释放v为入度的结点}for (k = j + 1; k <= G->vexnum; k++) // 对于adjvex域>j的结点，其序号-1{e.adjvex = k;p = Point(G->vertices[i].firstarc, e, equalvex, &p1); // Point()在func2-1.cpp中if (p)p->data.adjvex--; // 序号-1(因为前移)}}return OK;
}// 初始条件：图G存在，v和w是G中两个顶点
// 操作结果：在G中增添弧<v,w>，若G是无向的，则还增添对称弧<w,v>
Status InsertArc(struct ALGraph *G, VertexType v, VertexType w)
{struct ElemType e;int i, j;i = LocateVex(*G, v); // 弧尾或边的序号j = LocateVex(*G, w); // 弧头或边的序号if (i < 0 || j < 0)return ERROR;G->arcnum++; // 图G的弧或边的数目加1e.adjvex = j;e.info = NULL;   // 初值if (G->kind % 2) // 网{e.info = (int *)malloc(sizeof(int)); // 动态生成存放权值的空间printf("请输入弧(边)%s→%s的权值: ", v, w);scanf("%d", e.info);}ListInsert(&G->vertices[i].firstarc, 1, e); // 将e插在弧尾的表头，在bo2-8.cpp中if (G->kind >= 2)                           // 无向，生成另一个表结点{e.adjvex = i;                               // e.info不变ListInsert(&G->vertices[j].firstarc, 1, e); // 将e插在弧头的表头}return OK;
}// 初始条件：图G存在，v和w是G中两个顶点
// 操作结果：在G中删除弧<v,w>，若G是无向的，则还删除对称弧<w,v>
Status DeleteArc(struct ALGraph *G, VertexType v, VertexType w)
{int i, j;Status k;struct ElemType e;i = LocateVex(*G, v); // i是顶点v(弧尾)的序号j = LocateVex(*G, w); // j是顶点w(弧头)的序号if (i < 0 || j < 0 || i == j)return ERROR;e.adjvex = j;k = DeleteElem(&G->vertices[i].firstarc, &e, equalvex); // 在func2-1.cpp中if (k)                                                  // 删除成功{G->arcnum--;     // 弧或边数减1if (G->kind % 2) // 网free(e.info);if (G->kind >= 2) // 无向，删除对称弧<w,v>{e.adjvex = i;DeleteElem(&G->vertices[j].firstarc, &e, equalvex);}return OK;}else // 没找到待删除的弧{return ERROR;}
}Boolean visited[MAX_VERTEX_NUM]; // 访问标志数组(全局量)
void (*VisitFunc)(char *v);      // 函数变量(全局量)
// 从第v个顶点出发递归地深度优先遍历图G。算法7.5
void DFS(struct ALGraph G, int v)
{int w;visited[v] = TRUE;             // 设置访问标志为TRUE(已访问)VisitFunc(G.vertices[v].data); // 访问第v个顶点for (w = FirstAdjVex(G, G.vertices[v].data); w >= 0; w = NextAdjVex(G, G.vertices[v].data, G.vertices[w].data))if (!visited[w])DFS(G, w); // 对v的尚未访问的邻接点w递归调用DFS
}// 对图G作深度优先遍历。算法7.4
void DFSTraverse(struct ALGraph G, void (*Visit)(char *))
{int v;VisitFunc = Visit; // 使用全局变量VisitFunc，使DFS不必设函数指针参数for (v = 0; v < G.vexnum; v++)visited[v] = FALSE; // 访问标志数组初始化for (v = 0; v < G.vexnum; v++)if (!visited[v])DFS(G, v); // 对尚未访问的顶点调用DFSprintf("\n");
}typedef int QElemType; // 队列元素类型#if 1
typedef struct QNode
{QElemType data;     /* 数据域 */struct QNode *next; /* 指针域 */
} QNode, *QueuePtr;
typedef struct LinkQueue
{QueuePtr front; // 队头指针QueuePtr rear;  // 队尾指针
} LinkQueue;
void InitQueue(LinkQueue *Q);
void DestroyQueue(LinkQueue *Q);
void ClearQueue(LinkQueue *Q);
Status QueueEmpty(LinkQueue Q);
int QueueLength(LinkQueue Q);
Status GetHead(LinkQueue Q, QElemType *e);
void EnQueue(LinkQueue *Q, QElemType e);
Status DeQueue(LinkQueue *Q, QElemType *e);
void QueueTraverse(LinkQueue Q, void (*vi)(QElemType));
void print(QElemType i);
void InitQueue(LinkQueue *Q)
{                                                         // 构造一个空队列 QQ->front = Q->rear = (QueuePtr)malloc(sizeof(QNode)); /* 单链表的头结点 */if (Q->front == NULL)exit(-1);Q->front->next = NULL;
}
void DestroyQueue(LinkQueue *Q)
{while (Q->front){Q->rear = Q->front->next;free(Q->front);Q->front = Q->rear;}
}
void ClearQueue(LinkQueue *Q)
{QueuePtr p, q;Q->rear = Q->front;p = Q->front->next;Q->front->next = NULL;while (p){q = p;p = p->next;free(q);}
}
Status QueueEmpty(LinkQueue Q)
{if (Q.front->next == NULL)return TRUE;elsereturn FALSE;
}
int QueueLength(LinkQueue Q)
{int i = 0;QueuePtr p;p = Q.front;while (Q.rear != p){i++;p = p->next;}return i;
}
Status GetHead(LinkQueue Q, QElemType *e)
{QueuePtr p;if (Q.front == Q.rear)return ERROR;p = Q.front->next;*e = p->data;return OK;
}
void EnQueue(LinkQueue *Q, QElemType e)
{QueuePtr p;if (!(p = (QueuePtr)malloc(sizeof(QNode)))) // 存储分配失败exit(-1);p->data = e;p->next = NULL;    /* 新结点的 next 为空 */Q->rear->next = p; /* 上一次的尾指针指向新的结点 */Q->rear = p;       /* 新的尾指针 */
}
Status DeQueue(LinkQueue *Q, QElemType *e)
{QueuePtr p;if (Q->front == Q->rear)return ERROR;p = Q->front->next;*e = p->data;Q->front->next = p->next;if (Q->rear == p)Q->rear = Q->front;free(p);return OK;
}
void QueueTraverse(LinkQueue Q, void (*vi)(QElemType))
{QueuePtr p;p = Q.front->next;while (p){vi(p->data);p = p->next;}printf("\n");
}void print(QElemType i)
{// printf("%s ", i);
}
#endif//按广度优先非递归遍历图G。使用辅助队列Q和访问标志数组visited。算法7.6
void BFSTraverse(struct ALGraph G, void (*Visit)(char *))
{int v, u, w;LinkQueue Q;for (v = 0; v < G.vexnum; ++v)visited[v] = FALSE;        // 置初值InitQueue(&Q);                 // 置空的辅助队列Qfor (v = 0; v < G.vexnum; v++) // 如果是连通图，只v=0就遍历全图if (!visited[v])           // v尚未访问{visited[v] = TRUE;Visit(G.vertices[v].data);EnQueue(&Q, v);        // v入队列while (!QueueEmpty(Q)) // 队列不空{DeQueue(&Q, &u); // 队头元素出队并置为ufor (w = FirstAdjVex(G, G.vertices[u].data); w >= 0; w = NextAdjVex(G, G.vertices[u].data, G.vertices[w].data))if (!visited[w]) // w为u的尚未访问的邻接顶点{visited[w] = TRUE;Visit(G.vertices[w].data);EnQueue(&Q, w); // w入队}}}printf("\n");
}// 从第v个顶点出发递归地深度优先遍历图G。仅适用于邻接表存储结构
void DFS1(struct ALGraph G, int v, void (*Visit)(char *))
{struct ArcNode *p;                               // p指向表结点visited[v] = TRUE;                               // 设置访问标志为TRUE(已访问)Visit(G.vertices[v].data);                       // 访问该顶点for (p = G.vertices[v].firstarc; p; p = p->next) // p依次指向v的邻接顶点if (!visited[p->data.adjvex])DFS1(G, p->data.adjvex, Visit); // 对v的尚未访问的邻接点递归调用DFS1
}// 对图G作深度优先遍历。DFS1设函数指针参数
void DFSTraverse1(struct ALGraph G, void (*Visit)(char *))
{int v;for (v = 0; v < G.vexnum; v++)visited[v] = FALSE;        // 访问标志数组初始化，置初值为未被访问for (v = 0; v < G.vexnum; v++) // 如果是连通图，只v=0就遍历全图if (!visited[v])           // v尚未被访问DFS1(G, v, Visit);     // 对v调用DFS1printf("\n");
}// 按广度优先非递归遍历图G。使用辅助队列Q和访问标志数组visited。仅适用于邻接表结构
void BFSTraverse1(struct ALGraph G, void (*Visit)(char *))
{int v, u;struct ArcNode *p; // p指向表结点LinkQueue Q;       // 链队列类型for (v = 0; v < G.vexnum; ++v)visited[v] = FALSE;        // 置初值为未被访问InitQueue(&Q);                 // 初始化辅助队列Qfor (v = 0; v < G.vexnum; v++) // 如果是连通图，只v=0就遍历全图if (!visited[v])           // v尚未被访问{visited[v] = TRUE;         // 设v为已被访问Visit(G.vertices[v].data); // 访问vEnQueue(&Q, v);            // v入队列while (!QueueEmpty(Q))     // 队列不空{DeQueue(&Q, &u);                                 // 队头元素出队并置为ufor (p = G.vertices[u].firstarc; p; p = p->next) // p依次指向u的邻接顶点if (!visited[p->data.adjvex])                // u的邻接顶点尚未被访问{visited[p->data.adjvex] = TRUE;         // 该邻接顶点设为已被访问Visit(G.vertices[p->data.adjvex].data); // 访问该邻接顶点EnQueue(&Q, p->data.adjvex);            // 入队该邻接顶点序号}}}printf("\n");
}// 输出图的邻接矩阵G
void Display(struct ALGraph G)
{int i;struct ArcNode *p;switch (G.kind){case DG:printf("有向图\n");break;case DN:printf("有向网\n");break;case UDG:printf("无向图\n");break;case UDN:printf("无向网\n");}printf("%d个顶点：\n", G.vexnum);for (i = 0; i < G.vexnum; ++i)printf("%s ", G.vertices[i].data);printf("\n%d条弧(边):\n", G.arcnum);for (i = 0; i < G.vexnum; i++){p = G.vertices[i].firstarc;while (p){if (G.kind <= 1 || i < p->data.adjvex) // 有向或无向两次中的一次{printf("%s→%s ", G.vertices[i].data, G.vertices[p->data.adjvex].data);if (G.kind % 2) // 网printf(":%d ", *(p->data.info));}p = p->nextarc;}printf("\n");}
}/************************ end of file **************************/