一、Coq的安装与使用
1、Coq简介
Coq是一款交互式证明辅助工具,提供一套证明系统,可以编写证明、检查证明;也提供一套形式化语言,可编写数学算法、定义、定理;它还可以用于程序的正确性证明。
2、Coq的安装
Coq-8.11.0 安装包【Windows、MacOS】
链接:https://pan.baidu.com/s/1rAjW8D6G5GJI3sQP1JfG7g
提取码:ects
安装完成之后,Coq自带CoqIde,对于形式化方法课程来说应该是够用了。
【我有尝试使用另外一种IDE:Proof General,但是没有成功,等成功之后再来更新吧,目前就先用CoqIde了hhhh】
3、Warm-up Test
(1)创建一个名为 coq_warm_up.v 的文件,保存如下代码:
【其中 “.v” 是Coq文件的默认后缀】
Inductive day : Type :=
| monday : day
| tuesday : day
| wednesday : day
| thursday : day
| friday : day
| saturday : day
| sunday : day. Definition next_weekday (d:day) : day :=
match d with
| monday => tuesday
| tuesday => wednesday
| wednesday => thursday
| thursday => friday
| friday => monday
| saturday => monday
| sunday => monday
end.Eval compute in (next_weekday friday).
Eval compute in (next_weekday (next_weekday saturday)). (2)运行CoqIde,打开上述文件;
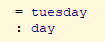
(3)单击 Go to end 按钮,会得到如下的输出:
= monday: day= tuesday: day此时说明Coq安装成功。
4、Coq功能分区
- Tool bar 工具栏:提供可执行的基本命令。
- Script buffers 脚本缓冲区:用于打开和编辑脚本。
- Goal window 目标窗口:显示待验证目标。
- Message window 消息窗口
二、Coq Tactics——如果使用Coq进行proof development
在proof development的每个阶段,都有一个要证明的子目标列表。
最初,该列表由所要证明的新定理的本身组成;
应用某些策略之后,目标列表包含该策略生成的子目标,接下来的工作就是分别对这些子目标进行处理。
主要包括以下策略:intros, apply, inversion, split, right and left。
A basic theorem:
Theorem ident body: type.
Proof.Tactics
Qed.-
Theorem - Coq中的一个命令,声明了一个需要证明的新定理;
-
ident - 新定理的名称;
-
body - 新定理的主体;
-
type -
forall 新定理中出现的变量名(多个变量用空格隔开):Prop,
所要证明的新定理.
-
Proof - 标示着证明新定理的开始
-
Tactics - 指导证明的过程,在结论和前提之间提出演绎规则,实现反向推理
-
Qed - 标示着证明新定理的完成
1、Implication(蕴含):intros and apply tactic
【蕴含的引入规则:intros】
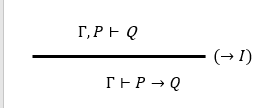
主要用于拆分所要证明定理中的已知前提和所要证明的结论。【详见下方】
【蕴含的删除规则:apply】
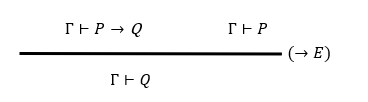
【详见下方】
第一个栗子:证明定理 P -> P成立
证明代码如下:
Theorem example1: forall P: Prop, P -> P.
Proof.intros.apply H.
Qed.
分析解释如下:
(1)执行前三行,结果如下:
由goal-window展示的结果可知,我们的证明目标位于水平线的下方。
横线上方没有任何的内容,表示 local context 为空,没有任何东西可以使用。
(2)执行intros策略:
基于当前目标,intros策略具有不同的效果,如果是:
forall T: type, T-> U
将 T: type 和 Hn: T 放入 local context,新的子目标就是U。
执行intros策略后,根据横线上方的内容,local context 中有两个前提可供使用。
(3)执行apply H:
在步骤(2)中,我们得到了一个名为H的假设,并且该假设的值与我们唯一的子目标相同,当我们得出与目标相同的假设时,使用 apply 策略。

(4)使用Qed命令完成证明:
当goal-window显示“No more subgoals”,表示证明过程结束,使用Qed命令完成证明,该命令可以让Qed保存定理及其证明。
相关练习:证明定理 P -> (Q -> P) 成立
Theorem exercise1: forall P Q:Prop,P -> (Q -> P).
Proof.intros.apply H.
Qed.(1)前三行:

(2)第四行:

此时发现子目标P和前提H相同,因此直接apply H即可。
(3)第五行:

第二个栗子:证明定理 (P -> Q) -> P -> Q 成立
证明代码如下:
Theorem example2: forall P Q: Prop,(P -> Q) -> P -> Q.
Proof.intros.apply H in H0.apply H0.
Qed.分析解释如下:
(1)执行前三行:

(2)执行第四行:
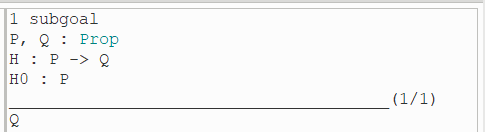
在local context中得到了两个假设,但是都和子目标不相同时:
如果我们知道: (a) x implies y,并且 (b) x 为真 时,我们可以使用 apply (a) in (b) 策略将(b)中的 x 转换为 y。
在本例中,
H: P -> Q
H0: P
由H可知,P implies Q,并且由H0可知,P为真,因此我们可以使用:
apply H in H0
将H0转换为Q。
即:将假设 H: P -> Q 应用于假设 H0: P,将假设H0变为Q。
(3)执行第五行:
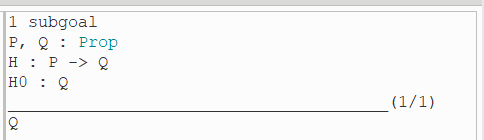
此时前提H0和子目标Q相同,apply H0 即可。
(4)执行第六行:

证毕。
相关练习:证明 P -> (Q -> ( H -> Q )) 成立
代码如下:
Theorem exercise2: forall P Q H:Prop,P -> (Q -> (H -> Q)).
Proof.intros.apply H1.
Qed.
2、Conjunction(合取、交):inversion(反演) and split(拆分) tactic
【合取的】
【合取的引入规则】

在Coq中使用这个命令就是将结论拆分成两个来证明,两个都需要进行证明。
第一个栗子:证明 P /\ Q -> Q 成立
证明代码如下:
Theorem example3: forall P Q: Prop,P/\Q -> Q.
Proof.intros.inversion H.apply H1.
Qed.分析解释如下:
(1)执行前三行:

(2)执行第四行:

【 inversion 策略 用法一】
inversion 策略用于证明具有 conjuction(合取、交)连接的定理。
执行完第四行之后,我们得到了一个假设 H: P /\ Q,其中具有合取运算符。
inversion 策略主要用于发现假设成立的前提。
有假设H可知,P /\ Q为真,只有在 P 为真并且 Q 为真的情况下,P /\ Q 才可能为真,因此我们可以使用 Inversion 策略向 local context 中添加两个假设—— H0: P H1: Q。
(3)执行第五行:

此时假设H1和子目标相同,因此只需要 apply H1 即可。
(4)执行第六行:

相关练习:证明 P /\ Q ->P 成立
代码如下:
Theorem exercise3: forall P Q: Prop,P /\ Q -> P.
Proof.intros.inversion H.apply H0.
Qed.
第二个栗子:证明 (P /\ Q) -> (Q /\ P)
证明代码如下:
Theorem example4: forall P Q:Prop,(P /\ Q) -> (Q /\ P).
Proof.intros.inversion H.split.apply H1.apply H0.
Qed.分析解释如下:
(1)执行前三行:

(2)执行第四行:
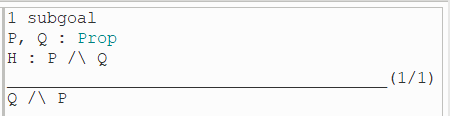
假设中包含合取运算符,因此使用 Inversion 策略。
(3)执行第五行:

我们需要证明的目标是 Q /\ P 成立,显然 Q /\ P 成立的条件是 Q 和 P 都为真,因此我们可以将目标拆分。
split 策略用于将目标拆分成几个子目标,然后再对子目标进行一一证明。
(3)执行第六行:
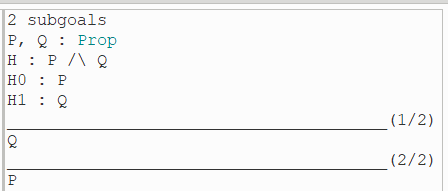
首先证明子目标Q,直接 apply H1 即可
(7)执行第七行:

再证明剩余的一个子目标P,apply H0
(8)执行第八行:

相关练习:证明 (P /\ (Q /\ R)) -> ((P /\ Q) /\ R) 成立
Theorem exercise4: forall P Q R:Prop,(P /\ (Q /\ R)) -> ((P /\ Q) /\ R).
Proof.intros.inversion H.inversion H1.split.split.apply H0.apply H2.apply H3.
Qed.
3、Disjunction(析取,并): right and left tactic
【析取的引入规则 left & right】
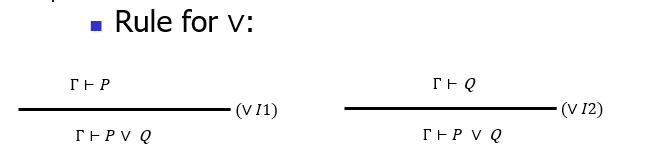
对目标结论输入 left,能够使得目标变成 P;同理对目标结论输入 right,能够使得目标变成 Q。
在实际操作时,选择一个证明起来比较简单的式子。
第一个栗子:证明 (P \/ Q) -> (Q \/ P) 成立
证明代码如下:
Theorem example5: forall P Q: Prop,(P \/ Q) -> (Q \/ P).
Proof.intros.inversion H.right.apply H0.left.apply H0.
Qed.分析解释如下:
(1)执行前三行:

(2)执行第四行:
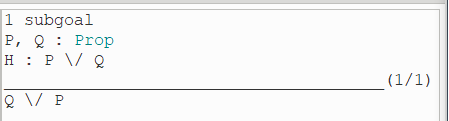
【 inversion 策略 用法二】
inversion 策略还可用于具有 disjunction(合取、并)连接的定理,生成两个具有相同结论、但 local context 中H0值不同的子目标。
(3)执行第五行:

第一个子目标需要我们在假设 H0: P 成立的前提下,证明 Q \/ P 为真,因此许需要证明 Q 为真或者 P 为真 或者 Q 和 P 均为真即可。
前提为 H0: P,需要证明的子目标 Q \/ P 中包含 P,且 P 位于合取符号的右侧,因此,使用 right 策略使得子目标与假设 H0 相同。
(4)执行第六行:
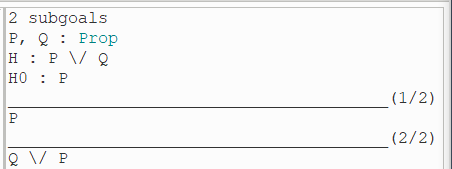
此时 前提 H0 与第一个子目标相同,因此只需要 apply H0 即可。
(5)执行第七行:

需要证明的目标为:在 H0: Q 成立的前提下,证明 Q \/ P 为真,Q 位于合取符号的左侧,因此使用 left 策略使得目标与假设 H0 相同。
(6)执行第八行:

(7)执行第九行:

相关练习:证明 (P \/ (Q \/ R)) -> ((P \/ Q) \/ R) 成立
代码如下:
Theorem exercise5: forall P Q R:Prop,(P \/ (Q \/ R)) -> ((P \/ Q) \/ R).
Proof.intros.inversion H.left.left.apply H0.inversion H0.left.right.apply H1.right.apply H1.
Qed.
4、not(~):unfold 策略
【使用场景】
当我们想要展开某个定义或者函数实现时,使用 unfold 策略。
当我们想要将 ~X 转换为 X -> False 时,使用 unfold 策略,有两种实现方法:
(1)unfold not
(2)unfold "~"
举个栗子:证明 P -> ~P -> Q 成立。
证明代码如下:
Theorem absurd: forall P Q:Prop,P -> ~P -> Q.
Proof.unfold not.intros.elim H0.apply H.
Qed.(1)执行前三行代码:

使用 unfold not 将 ~Q 转换为 Q -> False。
(2)执行第四行代码:

elim 策略用于消除谬误。
(3)执行第五行代码:

(4)执行第七行代码:

练习:
证明 ((P -> R) /\ (Q -> R)) -> (P /\ Q -> R) 成立。
Theorem exercise6: forall P Q R:Prop,((P -> R) /\ (Q -> R)) -> (P /\ Q -> R).
Proof.intros.inversion H0.inversion H.apply H3 in H1.apply H1.
Qed.
证明 (P -> Q /\ R) -> ((P -> Q) /\ (P -> R)) 成立。
Theorem exercise7: forall P Q R:Prop, (P -> Q /\ R) -> ((P -> Q) /\ (P -> R)).
Proof.intros.split.apply H.apply H.
Qed.
证明 ((P /\ Q) /\ R, S /\ T) -> (Q /\ S) 成立。
Theorem challenge1: forall P Q R S T:Prop,(((P /\ Q) /\ R) /\ (S /\ T)) -> (Q /\ S).
Proof.intros.inversion H.inversion H0.inversion H2.inversion H1.split.apply H5.apply H6.
Qed.
证明 (P -> Q) -> (~Q -> ~P) 成立。
证明代码如下:
Theorem challenge2: forall P Q:Prop,(P -> Q) -> (~Q -> ~P).
Proof.unfold not.intros.apply H in H1.apply H0 in H1.apply H1.
Qed.(1)执行前三行代码:

(2)执行第四行:

(3)执行第五行:

(4)执行第六行:
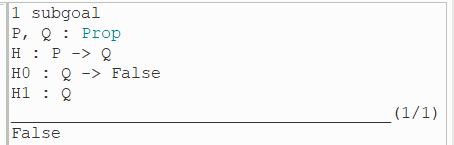
(5)执行第七行:

(6)执行第八行:

参考:
https://www.cnblogs.com/luluathena/archive/2010/08/19/1803065.html
http://www.doc88.com/p-5187845230295.html
https://zhuanlan.zhihu.com/p/33294417?edition=yidianzixun