【coq】函数语言设计笔记 06 -logic

article/2025/10/21 13:14:38

参考博客：https://www.cnblogs.com/TheFutureIsNow/p/11993851.html

Coq中的命题类型语句

Coq是一种类型化语言，这意味着它的世界中的每个合理表达式都有一个相关的类型。逻辑声明也不例外，任何一个可以证明的语句都有一个类型，即Prop，命题类型。
可以使用check命令查看这个类型：

在这里插入图片描述

需要注意的是，任何符合命题语法定义的语句都是Prop类型的，不论它们是否成立
命题Prop的构建方法：
• 使用表达式
• 使用已经定义的命题
• 带参数的命题

 
Check 2= 2.
Check (3 = 3) : Prop.Definition plus_claim : Prop := 2 + 2 = 4.
Check plus_claim : Prop.
Theorem plus_claim_is_true :plus_claim.
Proof. reflexivity.  Qed.

Check (forall n m : nat, n + m = m + n) : Prop.Check @eq : forall A : Type, A -> A -> Prop.Definition plus_claim : Prop := 2 + 2 = 4.
Check plus_claim : Prop.

然后可以在其他使用命题类型语句的地方用这个名称，比如[Theorem]语句中：
Theorem plus_claim_is_true :
plus_claim.
Proof. reflexivity. Qed.

还可以定义一些“带参数”的命题：

Definition injective {A B} (f : A -> B) :=forall x y : A, f x = f y -> x = y.
Lemma succ_inj : injective S.
//证明S 运算具有单射性质Proof.intros n m H. injection H as H1. apply H1.
Qed.

合取

合取
假设含合取-destruct / intros 时直接写
目标含合取-split

命题A和命题B的合取，也称为逻辑与，记为A/\B，只有当A和B同时成立的时候A/\B才成立：

Example and_example :3+4=7/\2*2=4.

如果证明目标是一个合取表达式，则需要使用[split]策略，它用于从合取表达式生成两个子目标：

Proof.split.- (* 3 + 4 = 7 *)reflexivity.- (* 2 + 2 = 4 *)reflexivity.
Qed.

对于任何命题A和B，假设A是成立的，并且B也是成立的，则可以得出结论，A/\B也是成立的：
在这里插入图片描述

该lemma and_intro 等价于 split
在这里插入图片描述

二者效果相同

如果需要用到的假设是一个合取表达式，那么可以使用[destruct]策略。如果证明上下文包含一个假设H，其形式为A/\B，那么destruct H as [HA HB]将把H从上下文中除去，并增加两个新的假设:HA，表示A为真；HB，表示B为真。

写法1
在这里插入图片描述

也可以在使用[intro]关键字的时候直接将上下文中的假设写成两个新的假设：
使用 [] ，把它们变成a single conjunction 单一连词
在这里插入图片描述

也可不使用 []
在这里插入图片描述

使用 [] 扔掉destruct中不需要的假设
连接词的另一种常见情况是，我们知道[A /\ B]，但在某些情况下我们只需要[A]或只需要[B]。在这种情况下，我们可以做一个[destruct]（可能是作为[intros]的一部分），并使用下划线模式[]来表示不需要的连接体应该被扔掉。
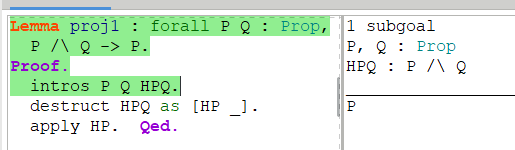
在这里插入图片描述

在这里插入图片描述

关于合取，一个必然成立的结论是：如果A/\B成立，那么A必然成立，或者B必然成立：
合取的性质
commutativity theorem 交换顺序
在这里插入图片描述

associativity theorem 结合律
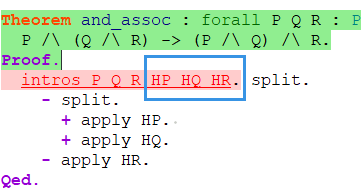
在这里插入图片描述

此时必须使用 [] 分隔假设

析取

假设中含析取，可以用[destruct]显式地进行，也可以用[intros]模式隐式地进行。
目标中含析取，使用[left] and [right]
在这里插入图片描述

引入 [left] and [right]

只需要证明其中一边的情况
在这里插入图片描述

需要均证明左右的情况
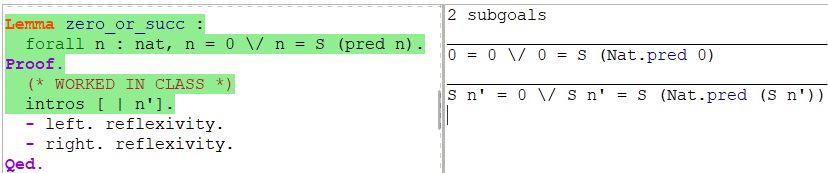
在这里插入图片描述

实例
在这里插入图片描述

假命题和否定 Falsehood and Negation

逻辑否定运算符¬ the logical negation operator

在前面的策略中有讲述过Coq中的[discriminate]策略时，提到过如果两个假设两个不同构造器构造的变量相等，那么就可以根据这个假设推导出任何结论，因为这个假设前提就是不成立的。
即不成立的前提可用于推导任何goal
即

Theorem ex_falso_quodlibet : forall (P:Prop),False -> P.

逻辑非~P定义成P->False，其中False是一个在Coq标准库中定义的一个矛盾命题 a contradictory proposition

Module MyNot.Definition not (P:Prop) := P -> False.Notation "~ x" := (not x) : type_scope.Check not : Prop -> Prop.End MyNot.

因为False是一个矛盾命题，那么根据前面所提到的那个原则，如果在证明过程中得到了一个矛盾命题False，那么可以直接使用[destruct]来完成整个证明目标：

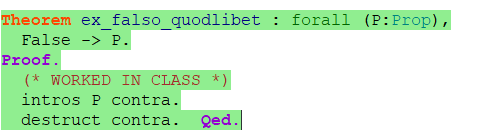
在这里插入图片描述

同样的，可以根据逻辑非来定义不相等：

Notation "x <> y":= (~(x = y)).

证明否命题

在这里插入图片描述

Definition not (P:Prop) := P -> False.

恒真命题

除了前面提到的矛盾命题，在coq标准库中也定义了恒真命题True：

Lemma True_is_true : True.
Proof.
(*To prove it, we use the predefined constant I : True:*)apply I.
Qed.```![在这里插入图片描述](https://img-blog.csdnimg.cn/b836972bb2a846f1b406dbb89dccd4d6.png)逻辑等价 Logical Equivalence
常见的“当且仅当”if and only if 逻辑连词，意味着两个命题有着相同的真值，可以将其定义为两个蕴含的合取：![在这里插入图片描述](https://img-blog.csdnimg.cn/f7c432911ada40819713853b79f367d9.png)逻辑等价的证明![在这里插入图片描述](https://img-blog.csdnimg.cn/bc9a380da53e43329869251ef6186fef.png)## 存在量词 Existential Quantification
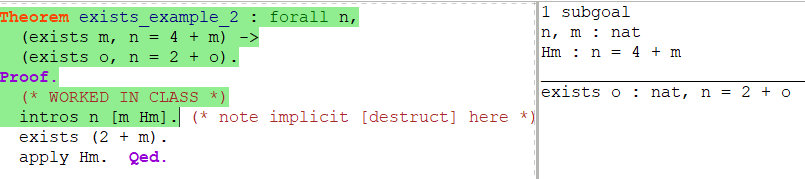
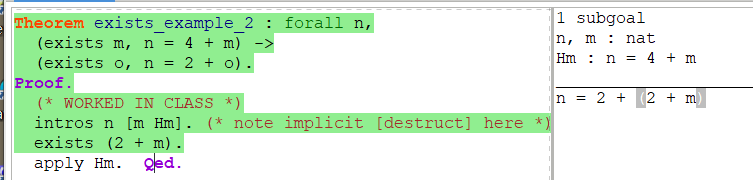
另外一个比较重要的逻辑连词是存在量词。如果说一个 T 类型的变量 x 满足属性 P，则记为 exists x:T, P。**goal 中有exist，则找出特例
假设中有exist，使用destruct ，得到x，把exists x:T, P 变成 已知x 证明 P 对x成立**
举例

Definition Even x :=
exists n : nat, x = double n.

为了证明形如exists x:T,P.类型的命题，必须要证明对于某个特定的x，P属性成立。这称为**存在的见证：**![在这里插入图片描述](https://img-blog.csdnimg.cn/a30b6935e2c14d80a0d70989ccb5e941.png)
![在这里插入图片描述](https://img-blog.csdnimg.cn/7fb2708bed7e4367b31eb3e8e66c2b79.png)相反的，如果假设中有存在量词exists x:T,P，那么可以使用[destruct]来获取一个存在见证x以及假设x,P：![在这里插入图片描述](https://img-blog.csdnimg.cn/67f06a7ad9114fe08cfc2a91e6243eb5.png)
![在这里插入图片描述](https://img-blog.csdnimg.cn/21ce2d3607894864b87f85d602959de9.png)