coq在设置里把这些都勾选上，写代码会好用很多

Check关键字输出待测类型的，可以输出一个十进制数，但是还是类型的显示罢了

Compute计算定义的函数的输出值

simpl关键字是为了化简的可视化罢了，即显示化简的中间过程，不用这个关键字，照样可以证明成功。

* coq中证明方式有这几个：化简证明方式（reflexivity，simple也有一定作用，化简就是指进一步运算一下或者变一个更简单表示形式），改写证明方式（rewrite）:通过分类分析（destruct，这个不是数学归纳法），等等,其实这也跟我们在试卷上面做证明题一样的这些方法

reflexivity关键字是执行一些化简，比如一些函数的展开，然后进行等号两边相等性的判断（即真正的证明），如果不写这个关键字，是不行的，会提示错误“未完成的证明”。

最好看的字体是Segoe UI字体，这个不会中文乱码与英文注释显示产生括号显示不全的现象。

这里说的量词指的是plus_o_n这个定理（已经证明过的）是需要输入量词n的，这里是想来运用于第2行的0+n，所以这里自动匹配上了n这个数给了定理充当量词。很明显这里o+n通过这个定理算出得到n了，然后用定理中的，右边的n改写左边的0+n，那么两边就直接相等了。

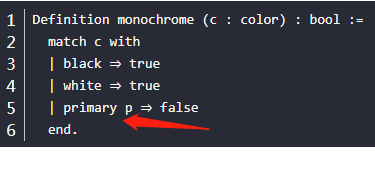
coq中的单竖线表示并列匹配项的意思，如下图。

上面 这个自然数比较函数，效果，若n,m相等，那么返回true，否则返回false。

 

注：在coq软件看来，一切都只是一些没有任何意义字母符号罢了，reflexivity也只是机械的化简一下（实际上就是运用一些已证明定理的宏替换罢了）检验等号两边的字符是否完全一样，从而得证。

上面在需要的地方才引入一个引理的作用就是：方便coq进行指定的字符进行机械替换罢了。

 

定义一个类型有只有一种方式：归纳定义（递归定义）

其中主要可以分为两种性质的类型：1、类似c语音的枚举类型那种，可以有限的一个一个把成员列举出来，比如

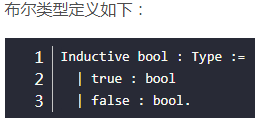
2、有无穷多个成员，没法一一列举出来的这种类型，递归的方式定义出来的，比如，列表（其成员数量可以无限）的定义：

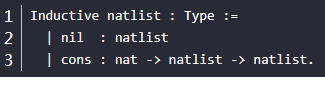
这里的形式cons : nat -> natlist -> natlist.是这样理解：cons为一个子构造函数（简称构造子），接收两个参数nat，natlist，输出一个结果natlist，其使用形式为cons nat natlist 为一个 natlist，其中这里的cons就是一个函数，注：这里cons nat natlist是一个整体，代表一个natlist，而不能省略掉cons这个构造函数名，例如下面图片的例子：primary就是color类型的一个构造子（就是一个函数）之一，而这个构造子有一个输入参数类型为rbg的元素（比如red，green，blue），输出一个结果color，所以primary red，primary green，primary blue都是color的一个成员，所以使用的时候应该是primary red等等这样连着写，不能省略掉primary或者red，green等，其使用例子如下。

               

继续讲列表的构造子nil : natlist形式的理解：nil也是一个子构造函数（简称构造子），代表没有输入参数，只有一个输出结果natlist。其使用形式为 nil 为一个 natlist。那么这里的nil只说是一个natlist，具体包含了几个元素呢，谁也不知道，此时只能看出nil是最基础（最原始）的一个natlist，而不能看出它是空列表（空列表只是coq内部自己指定了罢了，就像自然是的构造子O指定为了零0）。举例其使用：

这样就是人为的定义nil为空列表了。

Definition关键字是定义函数的，那么难道mylist是一个函数？这里我不太懂，但是cons，nil的用法已经体现出来了，就是当做构造器（也叫构造子，就是个函数）来使用。

 

再举一个自然数的定义的例子：

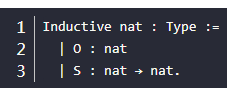
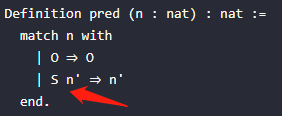
其实这里也只能看出O就是一个构造函数，没有输入参数，只有一个输出结果nat，既然没有输入参数（就跟列表定义的nil一样），那么就是最原始的自然数，也不能说它就是零0，coq是内置了代码把它当做数字0。而构造子S，有一个输入参数nat，输出结果为nat。那么其使用形式即：S O为一个nat，或者S (S O)为一个nat，其使用例子如下：

 

下面是一些进阶的定义和使用，做完最重要的科研内容，有空了继续研究吧，还有很多继续学习的地方，懂了上述说的内容，coq就入门了。做完最重要的科研内容，下次继续研究我收藏的两篇coq的CSDN博客。

我的测试代码：

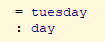
(* Inductive day : Type :=| monday| tuesday| wednesday| thursday| friday| saturday| sunday.Definition next_weekday (d:day) : day :=match d with| monday    => tuesday| tuesday   => wednesday| wednesday => thursday| thursday  => friday| friday    => monday| saturday  => monday| sunday    => mondayend.Compute (next_weekday friday).
(* ==> monday : day *)
-
Compute (next_weekday (next_weekday saturday)). *)
Check (S(S(S(S O)))).
Check (S O).Definition minustwo(n:nat):nat:=match n with|O=>O|S O=>O|S(S n')=>n'
end.
Compute(minustwo 4).Fixpoint evenb(n:nat):bool:=match n with|O=>true|S O=>false|S(S n')=>evenb n'
end.
Compute(evenb 4).
Check (evenb 4).Definition oddb(n:nat):bool:=negb(evenb n).
Example test_oddb1:oddb 2=false.
Proof. simpl. reflexivity. Qed.Fixpoint minus(n m:nat):nat:=match n,m with|O,_=>O|S_,O=>n|S n',S m'=>minus n' m'end.
Notation "x - y":=(minus x y)(at level 50,left associativity).
Example testMinus:minus 5 3=2.
Proof. simpl. reflexivity. Qed.Fixpoint plus(n m:nat):nat:=match n with|O=>m|S n'=>S (plus n' m)end.
Notation "x + y":=(plus x y)(at level 50,left associativity).Theorem plus_n_O_firsttry : forall n:nat,n = n + 0.
Proof.intros n.simpl. (* Does nothing! *)
Abort.Theorem plus_n_O_secondtry : forall n:nat,n = n + 0.
Proof.intros n. destruct n as [| n'].- (* n = 0 *)reflexivity. (* so far so good... *)- (* n = S n' *)simpl.       (* ...but here we are stuck again *)
Abort.Theorem plus_n_O : forall n:nat, n = n + 0.
Proof.intros n. induction n as [| n' IHn'].- (* n = 0 *)    reflexivity.- (* n = S n' *) simpl. rewrite <- IHn'. reflexivity.  Qed.Theorem minus_diag : forall n,minus n n = 0.
Proof.(* WORKED IN CLASS *)intros n. induction n as [| n' IHn'].- (* n = 0 *)simpl. reflexivity.- (* n = S n' *)simpl. rewrite -> IHn'. reflexivity.  Qed.

 

参考文章 

* 通过《Software Foundation》学习Coq语言的基本用法——1.Basics

* 通过《Software Foundation》学习Coq语言的基本用法——2.Induction 3.Lists