网络号的计算

article/2025/10/22 15:10:43

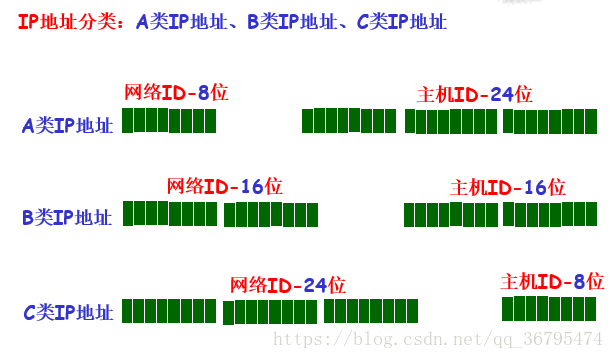
子网掩码和ip地址结合使用,可区分出一个网络的网络号和主机号.

例如:
有一个c类地址为: 192.9.200.12
默认子网掩码为: 255.255.255.0

① 将IP地址转化为二进制: 11000000 00001001 11001000 00001100
② 将子网掩码转换为二进制:11111111 11111111 11111111 00000000
③ 将子网掩码取反:00000000 00000000 00000000 11111111
④ 将①②二进制数逻辑相与: 11000000 00001001 11001000 00000000
转换为十进制:192.9.200.0
所以网络号为:192.9.200.0
⑤ 将子网掩码取反后再与IP地址逻辑相与
相与后得:00000000 00000000 00000000 00001100→0.0.0.12
所以主机号为12.

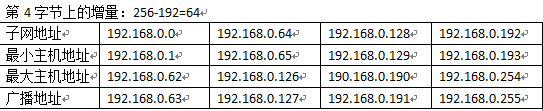
在这里插入图片描述
例如，有两台主机，
主机一的IP地址为222.21.160.6，子网掩码为255.255.255.192
主机二的IP地址为222.21.160.73，子网掩码为255.255.255.192。
主机一要给主机二发送数据，先要判断两个主机是否在同一网段。

主机一
222.21.160.6即：11011110.00010101.10100000.00000110
255.255.255.192即：11111111.11111111.11111111.11000000
按位逻辑与运算结果为：11011110.00010101.10100000.00000000
十进制形式为（网络地址）：222.21.160.0

主机二
222.21.160.73 即：11011110.00010101.10100000.01001001
255.255.255.192即：11111111.11111111.11111111.11000000
按位逻辑与运算结果为：11011110.00010101.10100000.01000000
十进制形式为（网络地址）：222.21.160.64

C类地址判断前三位是否相同，即可确定2个IP地址是否在同一网段内，但本例中的222.21.160.6与222.21.160.73不在同一网段，因为这两个C类IP地址已经做了子网划分就不能只判断前三个字节是否相同就确认这两个IP是否在同一网段。其中222.21.160.6在222.21.160.1-222.21.160.62 段，222.21.160.73在222.21.160.65-222.21.160.126 段，所以不在同一网段，如果要通信需要通过路由器转发。