离散数学——coq学习笔记（一）

article/2025/10/21 13:15:45

Coq学习笔记（一）

  • BASICS
    • 函数编程
    • 枚举类型
      • 引例：Days of the week（定义一个类型）
    • 一些基础语法定义
      • Type
      • Check命令
      • 多元组
      • Modules
      • Compute命令
      • 定义一个新常量
  • BOOLEANS
    • 布尔表达式的构造
      • 相关定义
      • 布尔表达式的相关运算律
      • 用Example检查计算结果是否符合预期
  • 课堂实例
    • 自然数和链表的递归构造
      • 自然数
      • 链表的构造
  • 参考书目课后题答案

OMG,没学离散数学之前觉得这就是门数学，学了之后被逻辑和编程同时吊打，这里根据一些资料把之前学的coq相关规则回顾一遍，毕竟要准备期末考试复习了，这学期东西又难又是在线上教学，一定要好好加油鸭。（鬼姐姐根本没在怕的）
所用参考书目为 《Logic Foundations》

BASICS

函数编程

函数编程强调让我们了解如何将输入映射到输出，同时将函数（方法）作为一级值（类似于数字，集合都属于数学中某一级别的值），也就是将函数作为数据来处理。
函数式编程思想也包括我们在OOP中涉及到的多态，代码重用，但是函数式编程是通过函数将程序模块化。

枚举类型

coq内置特性非常少，并没有像高级语言一样已经定义了常用的数据类型，而是提供了一种强大的机制来从头定义新的数据类型。
当然coq标准库提供了原始的数据类型，但我们这里选择显式地重述定义。

引例：Days of the week（定义一个类型）

defining a new set of data values-a type

Coq < Inductive day:Type:=
Coq < |monday
Coq < |tuesday
Coq < |wednesday
Coq < |thursday
Coq < |friday
Coq < |saturday
Coq < |sunday.
day is defined
day_rect is defined
day_ind is defined
day_rec is defined
  1. coq代码中经常会用数据：类型的格式展现一个数据和其相应的类型
  2. “：=”在coq中表示等于，用"."结束语句
  3. 这里定义了一个新的类型，名字是day，有七个成员
    用coq定义一个函数对这些数据进行操作
Definition next_weekday (d:day) : day :=match d with| monday => tuesday| tuesday => wednesday| wednesday => thursday| thursday => friday| friday => monday| saturday => monday| sunday => mondayend.

1 定义函数 Definition fun_name (输入）：（返回），注意这里的输入输出依然采用数据名称：数据类型的格式，但是一旦命名的数据名称必须在环境中使用（比如d），对于输入，一般都需要使用一个数据，需要说明数据，但是类型可有可无，对于输出，必须说明其类型（coq可以进行类型判断，但是我们一般会包括他们，使阅读更加容易）
2 在定义每个情况的输出类型时，必须定义所有可能的情况，比如这里需要列举所有星期对应的返回值。
定义好一个函数后，我们使用Compute命令对结果进行查询。

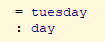
Compute (next_weekday friday).
Compute (next_weekday (next_weekday saturday)).

调用函数的时候和高级语言格式很接近。
执行结果：
在这里插入图片描述
在这里插入图片描述

一些基础语法定义

Type

每个表达式都有一个类型

  • New Types from Old
    就像前面定义的Days of week一样，我们定义的都是枚举类型的例子

Check命令

确定输入内容的类型

  • 简单的类型
Coq < Check True.
True: PropCoq < Check 3.
3: natCoq < Check 3+2.
3 + 2: nat
  • 有序数对
Coq < Check (2,3=5).
(2, 3 = 5): nat * Prop
  • 函数类型
    1 使用关键字fun构造一个新函数，它将替换λlambda微积分（之前的博客有提到）和类似理论的符号。
    they are written with arrows.
Coq < Check (fun x:nat=>x=3).
fun x : nat => x = 3: nat -> Prop
Coq < Check (forall x:nat,x<3\/(exists y:nat,x=y+3)).
forall x : nat, x < 3 \/ (exists y : nat, x = y + 3): Prop

2 let的使用（为函数提供一个临时的名字，之前的博客提到过）

Check (let f := fun x => (x * 3,x) in f 3).
let f := fun x : nat => (x * 3, x) in f 3 : nat * nat

3 构造枚举类函数时其成员也可以定义成一个函数（constructor)

Inductive reb:Type :=
|red
|green
|blue.Inductive color :Type:=
|black
|white
|primary (p:reb).
Check primary red.
Check primary blue.

多元组

多个参数的单个构造函数用于创建元组类型
比如我们在用二进制编码时，可以将某一位定义是取值为0或1的函数，那样我们表示一个字节时相当于八位的元组，很像在高级语言中的数组

Inductive bit:Type :=
|B0
|B1.
Inductive byte:Type :=
| bits(b0 b1 b2 b3 b4 b5 b6 b7:bit).
Check (bits B0 B1 B0 B1 B0 B1 B0 B1).

下划线的使用，我们用下划线代替未定义的变量，比如我们要检查定义的字节是否各位为全0

Definition all_zero (input:byte):bool:=
match input with
|(bits B0 B0 B0 B0 B0 B0 B0 B0)=>true
|(bits _ _ _ _ _ _ _ _)=>false
end.
Compute all_zero(bits B1 B1 B1 B1 B1 B1 B1 B1).

Modules

本课程中涉及很少

Compute命令

定义一个新常量

Coq < Definition example:=fun x=>x*x.
example is definedCoq < Compute example 1.= 1: natCoq < Compute example 3.= 9: nat

BOOLEANS

布尔表达式的构造

相关定义

  • 构建布尔集合，归纳定义布尔集合
Coq < Inductive bool:Type:=
Coq < |true
Coq < |false.
bool is defined
bool_rect is defined
bool_ind is defined
bool_rec is defined
  • 定义布尔运算
Coq < Definition negb b:=
Coq < match b with
Coq < |true=>false
Coq < |false=>true
Coq < end.
negb is definedCoq <  Definition andb n m:=
Coq < match n with
Coq < |true=>m
Coq < |false=>false
Coq < end.
andb is definedCoq < Definition orb n m :=
Coq < match n with
Coq < |true=>true
Coq < |false=>m
Coq < end.
orb is definedCoq < Compute orb true false.= true: bool
Coq < Compute negb true.= false: bool

插入标记

Coq <  Notation "n | m" := (andb n m)(at level 85,right associativity).Coq < Notation "n & m":=(andb n m)(at level 80,right associativity).Coq <  Notation "\ n":=(negb n)(at level 70,right associativity).Coq < Check true & false | \true.
(true & false) & \ true: boolCoq < Compute true & false | \true.= false: bool

定义计算级别和结合顺序

布尔表达式的相关运算律

用Example检查计算结果是否符合预期

Coq < Example test1: orb true false=false.
test1 < Proof. simpl. reflexivity. Qed.

课堂实例

自然数和链表的递归构造

自然数

  • 自然数的构造
    1 自然数的内部表示
Inductive nat:Type:=
|o
|S(n:nat).
(*O和S只是一种表达方式，O是归纳基础，S是构造算子，我们甚至可以这样定义*)
Inductive nat':Type:=
|Lilghost
|darling (d:nat').
Check darling(darling(darling Lilghost)).

递归定义：O是归纳基础，S是构造算子

Coq < Check 1.
1: nat
Coq <  Check S(S(S O)).
3: nat

coq内部用一进制表示自然数（上边那个是O不是0）
我们使用命令

Print nat.

可以输出nat的内部表示

Coq < Print nat.
Inductive nat : Set :=  O : nat | S : nat -> natFor S: Argument scope is [nat_scope]

Unset Printing Notations.
Set Printing Notations.

表示打开其内部表示

Coq < Unset Printing Notations.Coq < Check 3.
S (S (S O)): nat

2 一些关于自然数的函数

  • 前置函数
  • 利用递归函数确定给定自然数是否为偶数

3 定义自然数的加法
加法的定义：取m的n次后继
定义递归函数时用Fixpoint命令

Fixpoint plus n m := 
match n with
| O => m
| S n' => S (plus n' m)
end.
Compute plus 2 3.
Notation "x + y":=(plus x y).
Compute 2+3.

使用Notation能用符号表示函数

  • 练习：使用递归定义自然数乘法，减法
    练习答案：
Coq < Fixpoint plus n m:=
Coq < match n with
Coq < |O=>m
Coq < |S n'=>S (plus n' m)
Coq < end.
plus is defined
plus is recursively defined (decreasing on 1st argument)Coq <  Fixpoint mulit n m:=
Coq < match n with
Coq < |1=>m
Coq < |S n'=>plus m (mulit n' m)
Coq < |O=>O
Coq < end.
mulit is defined
mulit is recursively defined (decreasing on 1st argument)Coq < Compute mulit 3 5.= 15: natCoq < Notation "n * m":=(mulit n m).Coq < Compute 3*0.= 0: natCoq < Compute 5*9.= 45: nat

Coq < Fixpoint sub n m :=
Coq < match n,m with
Coq < |O,_=>O
Coq < |_,O=> n
Coq < |S x',S y'=>sub x' y'
Coq < end.
sub is defined
sub is recursively defined (decreasing on 1st argument)Coq < Compute sub 5 2.= 3: nat

递归是函数式编程的基本理念，保证函数的终止性，没有传统过程语言的循环结构

链表的构造

Inductive natlist : Set :=
| nil : natlist
| cons : nat -> natlist -> natlist.Definition l1 := cons 2 (cons 1 nil).(* syntax tree of l1 is: cons |+-----+-----+ |           |2         cons|+---+---+|       |1      nil
*)Definition l2 := cons 3 nil.Compute l1.Notation "[ ]" := nil.
Notation "[ a ; .. ; b ]" := (cons a .. (cons b nil) .. ).Compute l1.Fixpoint plus s t := match s with| [] => t| cons a s' => cons a (plus s' t)end.Compute plus [3] [2;1].Notation "x + y" := (plus x y).Compute l2 + l1.Fixpoint rev s := match s with| [] => []| cons a s' => (rev s') + [a]end.Compute rev (l2 + l1).
  • 练习：计算链表长度，自然数链表元素求和。
Coq < Fixpoint plus n m:=
Coq < match n with
Coq < |O=>m
Coq < |S n'=>S(plus n' m)
Coq < end.
plus is defined
plus is recursively defined (decreasing on 1st argument)Coq < Inductive list:Set:=
Coq < |nil:list
Coq < |cons :nat->list->list.
list is defined
list_rect is defined
list_ind is defined
list_rec is definedCoq <  Definition l1:=cons 2(cons 1(cons 3 nil)).
l1 is definedCoq <  Fixpoint nons s :=
Coq <  match s with
Coq < |nil=>O
Coq < |cons a s'=>plus 1 (nons s')
Coq < end.
nons is defined
nons is recursively defined (decreasing on 1st argument)Coq < Compute nons l1.= 3: natCoq <  Fixpoint sum s :=
Coq < match s with
Coq < |nil=>O
Coq < |cons a s'=>plus a (sum s')
Coq < end.
sum is defined
sum is recursively defined (decreasing on 1st argument)Coq < Compute sum l1.= 6: nat

参考书目课后题答案

  • EX1：standard (nandb)
Definition negb b:=
match b with
|true=>false
|false=>true
end.Definition nandb (b1:bool) (b2:bool) : bool :=
match b1 with
|false=>true
|true=>negb b2
end.
Example test_nandb1: (nandb true false) = true.
Proof. simpl. reflexivity. Qed.
Example test_nandb2: (nandb false false) = true.
Proof. simpl. reflexivity. Qed.
Example test_nandb3: (nandb false true) = true.
Proof. simpl. reflexivity. Qed.
Example test_nandb4: (nandb true true) = false.
Proof. simpl. reflexivity. Qed.
  • EX2： standard (andb3)
Definition andb n m:=
match n with
|true=>m
|false=>false
end.Definition andb3 (b1:bool) (b2:bool) (b3:bool) : bool :=
match b1 with
|false=>false
|true=>andb b2 b3
end.
Example test_andb31: (andb3 true true true) = true.
Proof. simpl. reflexivity. Qed.
Example test_andb32: (andb3 false true true) = false.
Proof. simpl. reflexivity. Qed.
Example test_andb33: (andb3 true false true) = false.
Proof. simpl. reflexivity. Qed.
Example test_andb34: (andb3 true true false) = false.
Proof. simpl. reflexivity. Qed.
  • EX3 standard (factorial)
Fixpoint muti m n:=
match m with
|O=>O
|S m'=>(plus n (muti m' n))
end.Fixpoint factorial (n:nat) : nat:=
match n with 
|O=>1
|S n'=>(muti n (factorial n'))
end.
Example test_factorial1: (factorial 3) = 6.
Proof. simpl. reflexivity. Qed.
Example test_factorial2: (factorial 5) = (mult 10 12).
Proof. simpl. reflexivity. Qed.Fixpoint eqb (n m:nat):bool:=
match n with
|O=>match m with |O=>true|S m'=>falseend
|S n'=>match m with|O=>false|S m'=>(eqb n' m')end
end.Compute (eqb 3 5).
  • EX4
Fixpoint eqb (n m:nat):bool:=
match n with
|O=>match m with |O=>true|S m'=>falseend
|S n'=>match m with|O=>false|S m'=>(eqb n' m')end
end.Definition ltb (n m : nat) : bool:=
match (minus n m)with 
|O=>(negb(eqb n m))
|_=>false
end.
Notation "x <? y" := (ltb x y) (at level 70) : nat_scope.
Example test_ltb1: (ltb 2 2) = false.
Proof. simpl. reflexivity. Qed.
Example test_ltb2: (ltb 2 4) = true.
Proof. simpl. reflexivity. Qed.
Example test_ltb3: (ltb 4 2) = false.
Proof. simpl. reflexivity. Qed.

终于结束第一部分了，接下来是coq独特的证明功能，本篇代码中间隐藏了数个小彩蛋，鬼姐姐们可以找找噢。


http://chatgpt.dhexx.cn/article/bt3wpZIO.shtml

相关文章

求网络号、子网号、主机号、子网网络地址、子网广播地址

求网络号、子网号、主机号、子网网络地址、子网广播地址

例题&#xff1a;某计算机的IP地址为10.38.51.21&#xff0c;子网掩码为255.255.0.0&#xff0c;写出该计算机的网络号、子网号、主机号以及子网网络地址、子网广播地址。 网络号&#xff1a;10子网号&#xff1a;38主机号&#xff1a;51.21子网网络地址&#xff1a;10.38.0.0子…
阅读更多...
根据子网掩码算出 IP 地址 的网络号和主机号

根据子网掩码算出 IP 地址 的网络号和主机号

我们如何根据子网掩码算出 IP 地址 的网络号和主机号呢&#xff1f; 举个例子&#xff0c;比如 10.100.122.0/24&#xff0c;后面的/24表示就是 255.255.255.0 子网掩码&#xff0c;255.255.255.0 二进制是「11111111-11111111-11111111-00000000」&#xff0c;大家数数一共多…
阅读更多...
关于IP地址、网络号、主机号、子网掩码之间的关系

关于IP地址、网络号、主机号、子网掩码之间的关系

IP地址类似于我们的身份证号码 国家为了唯一确定我们每个人的身份&#xff0c;会为我们每个人分配一个唯一确定身份的号码&#xff0c;同理&#xff1a; 为了确切地标识Internet&#xff08;互联网&#xff09;中的每一台主机和路由器&#xff0c;TCP/IP建立了一套编址方案&a…
阅读更多...
关于IP网络号和主机号的原理

关于IP网络号和主机号的原理

网络号和主机号具体怎么弄出来的? ? ? ? 1、标准分类的ip地址的网络号是&#xff0c; A类是前8位 B类是前16位 C类是前24位 举一个例子 如172.16.10.2&#xff0c;因为172.16.10.2是B类地址&#xff0c;所以172.16所代表的位就是网络号的位&#xff0c;后面10.2代表的…
阅读更多...
子网划分以及网络号的计算

子网划分以及网络号的计算

目录 一、子网划分的作用 1.计算网络号&#xff0c;通过网络号选择正确的网络设备连接终端设备 2.根据网络的规模&#xff0c;可以对局域网(内网)进行网络地址规划 二、IP地址 1.IP地址的组成部分 2.IP地址的版本 三、IP地址的分类 1.IP地址分类 2.IP地址分类总结思维…
阅读更多...
网络号，网络标识，广播地址，有效主机范围计算

网络号，网络标识，广播地址，有效主机范围计算

网络计算 IP 地址计算网络号&#xff0c;网络标识&#xff0c;有效主机范围IP地址分类 IP 地址 IP地址&#xff1a;网络部分主机部分 网络部分&#xff1a;确定终端是不是在同一网段 主机部分&#xff1a;用来确定终端的容量大小&#xff08;最多可以容纳多少台&#xff09; 同…
阅读更多...
网络号、主机号、子网号--例题

网络号、主机号、子网号--例题

已知 IP&#xff1a;195.169.20.50 子网掩码&#xff1a;255.255.255.224 求网络号 子网号 主机号。答&#xff1a; IP为C类&#xff0c;一知道子网掩码值是224 所以网络被划分为8个子网网络号是用将你的IP和子网掩码255.255.255.224的二进制进行逻辑与运算得到转换为十进制为…
阅读更多...
计算机网络：根据IP和子网掩码计算网络号

计算机网络：根据IP和子网掩码计算网络号

题目感觉有误&#xff0c;但是解题思路是正确的。 已知B类地址的子网掩码为255.255.0.0&#xff0c;假设某B类地址为127.24.36.55&#xff0c;那么它的网络号为&#xff1a;&#xff08;&#xff09; A、127.24.0.0 B、0.0.36.55 C、255.255.36.55 D、127.24.36.55 解题思路&…
阅读更多...
网络号和主机号具体计算原理-ipv4篇

网络号和主机号具体计算原理-ipv4篇

来自之前163网易博客&#xff0c;因博客倒闭&#xff0c;放CSDN供 大家学习。 1、标准分类的ip地址的网络号是&#xff0c; A类是前8位 B类是前16位 C类是前24位 举一个例子 如172.16.10.2&#xff0c;因为172.16.10.2是B类地址&#xff0c;所以172.16所代表的位就是网络号的位…
阅读更多...
网络号的计算

网络号的计算

子网掩码和ip地址结合使用,可区分出一个网络的网络号和主机号. 例如: 有一个c类地址为: 192.9.200.12 默认子网掩码为: 255.255.255.0 ① 将IP地址转化为二进制: 11000000 00001001 11001000 00001100 ② 将子网掩码转换为二进制:11111111 11111111 11111111 00000000 ③ 将子…
阅读更多...
计算机网络号的学习

计算机网络号的学习

目录 一、子网的划分 1.1子网划分的作用 二、相同网络与不同网络 1、相同网络 2、不同网络 三、IP地址的组成与作用 1、IP地址的组成 2、各组成的作用 四、IPV4地址与IPV6地址 五、IP地址的分类 六、IP地址按用途分类 七、网络号的计算方法 八、网络地址的划分 1…
阅读更多...
计算机网络中的子网号和网络号

计算机网络中的子网号和网络号

IP地址是一个32为的二进制数。 IP地址&#xff1d;网络id 主机id 网络号 网络号就是网络id&#xff0c;是某个互联网中子网的地址&#xff0c;通过子网掩码和IP地址按位“与”得到。 如192.9.200.13/24&#xff0c;子网掩码为255.255.255.0&#xff0c;该IP地址的网络号就是1…
阅读更多...
认识网络号与子网划分

认识网络号与子网划分

目录 一、计算机网络号 二、网络号的构成 1.认识网络号 &#xff08;1&#xff09;IP地址 &#xff08;2&#xff09;子网掩码 &#xff12;.IP地址用途分类 &#xff08;&#xff11;&#xff09;私有地址 &#xff08;&#xff12;&#xff09;公有地址 三、网络号的…
阅读更多...
IP地址、网络号、主机号、网络地址、子网掩码、网关、192.168.0.1/24是什么意思

IP地址、网络号、主机号、网络地址、子网掩码、网关、192.168.0.1/24是什么意思

IP地址 IP地址通俗上讲&#xff0c;就是台电脑在网络世界的唯一标识&#xff0c;它由32的二进制数组成&#xff0c;也就是4个字节&#xff0c;就像人的身份证一样&#xff0c;它能够唯一标识一台电脑。 IP地址的组成 IP地址网络ID主机ID&#xff0c;同一个网络的IP地址能够公用…
阅读更多...
正方形的展开图

正方形的展开图

记得这个题目是我小学竞赛的最后一个题目&#xff0c;当时这个题目没有做出来 (^_^) 正方形的展开图共有11种。 分下面的4种情况&#xff1a;
阅读更多...
正方体展开图

正方体展开图

阅读更多...
如何用几何画板作正方体的动态展开图

如何用几何画板作正方体的动态展开图

在教学中&#xff0c;为了增强教学效果&#xff0c;通常用折纸法演示正方体的展开与折叠过程&#xff0c;这样的做法对学生的理解还是起不了多大作用的。如果可以借助一些教学辅助工具制作模型进行演示&#xff0c;那效果肯定更为显著。几何画板就是符合这样要求的教学辅助工具…
阅读更多...
矩形可以切割多少个最大的正方形

矩形可以切割多少个最大的正方形

本题为填空题&#xff0c;只需要算出结果后&#xff0c;在代码中使用输出语句将所填结果输出即可。 题目描述 小明有一些矩形的材料&#xff0c;他要从这些矩形材料中切割出一些正方形。 当他面对一块矩形材料时&#xff0c;他总是从中间切割一刀&#xff0c;切出一块最大的正…
阅读更多...
画出一个正方形

画出一个正方形

1.新建TankFrame类继承Frame类方便重写里面的方法 2.创建一个构造方法 3.把Main方法里的设置剪切进刚刚定义的构造方法&#xff08;快捷键CtrlX&#xff09;并修改里面的方法&#xff0c;并把f.删掉 import java.awt.*; import java.awt.event.WindowAdapter; import java.awt…
阅读更多...
从矩形中切割出最大的正方形

从矩形中切割出最大的正方形

样例如图 #include <iostream> #include <string> #include <cmath> using namespace std;string input[2010]; int lt[2010][2010]; int up[2010][2010];int Find(int n,int m) {int Max1;for(int i0;i<n;i){for(int j0;j<m;j){if(i0&&j0){lt…
阅读更多...
推荐文章

Copyright @ 2022~2023