---

前言

本文的主要内容是自适应数字滤波器的介绍，包含其特点与构成、最陡下降法、最小均方算法以及最小二乘算法等内容。

---

一、自适应滤波器的特点和构成

自适应滤波器的特点： 滤波器的参数可以自动地按照某种准则调整到最佳滤波；实现时不需要任何关于信号和噪声的先验统计知识，尤其当输入统计特性未知，调整自身参数到最佳的过程称为“学习过程”。将输入信号统计特性变化时，调整自身的参数到最佳的过程称为“跟踪过程”，因此自适应滤波器具有学习和跟踪的性能。
自适应滤波器的构成： 主要有两部分，第一部分的主要执行部件是一个FIR或IIR结构的滤波器，完成的实质工作就是滤波，其中滤波器的权系数是可以随时进行调整的；第二部分是滤波器权系数的调整算法(学习算法)，由误差信号和输入信号一起构成校正量，自适应的调整权系数，使误差信号趋于降低的趋势，从而使滤波器逐渐达到或接近最优滤波器。
自适应滤波器主要归为4类应用：辨识、线性预测、均衡、干扰消除。

---

二、最陡下降法

最陡下降法也称梯度下降法，其通过自适应改变权系数来寻找最佳权系数，权系数的更新是向着性能函数(均方误差)的负梯度方向进行的。
最陡下降法的递推公式：

j+1时刻的权矢量W_j+1等于j 时刻的权矢量W_j加上一个负梯度变换量。
μ是调整步长的常数，它控制着系统的稳定性和自适应的收敛速度。
梯度的方向是性能函数增加最快的方向，负梯度的方向就是性能函数减小最快的方向。

每一步权系数的调整算法：

上式就是每一步权系数的调整算法，或称学习算法，通过这个算法不断调整权系数，最终使权系数收敛到最优权系数（维纳权系数）。
学习算法的关键是，在什么条件下算法是收敛的，或分析保证收敛的情况下迭代步长的取值范围。
最陡下降法的收敛条件：

其中ʎ_max是R_xx的最大特征值。

上式是时间常数，它的值越大，函数收敛的越慢。
取近似如下：

如果输入信号的自相关矩阵的特征值很分散时，算法的收敛速度很慢，当特征值比较紧凑时，收敛速度较快。

---

三、最小均方算法(LMS)

最小均方算法或LMS(Least Mean Square)算法结构简单，可收敛，能满足许多实际应用的需求，但也存在收敛速度较慢，有额外
误差等缺点。
最陡下降法虽然可以收敛到最优滤波器，但其迭代过程需要先验的自相关矩阵和互相关矩阵，这在实际中难以实现。
均方误差的获取是困难的，在实际应用中，采用单次样本误差的平方来代替均方误差，并以单次误差平方的梯度代替均方误差的梯度，这就是LMS算法，也叫随机梯度法。
LMS算法的权值计算：

LMS算法的梯度估计值用单次误差信号进行计算：

j 时刻的梯度是由 j 时刻的误差信号和 j 时刻的输入矢量信号估计出来的，所以梯度的估计值具有随机性。
滤波器权系数的递推公式：

将梯度表达式代入上式得到最小均方算法表达式：

LMS自适应滤波(FIR结构)算法总结：

LMS算法具有运算量小的显著优点。
LMS中梯度的估计值是无偏估计。
LMS算法中权矢量是在最陡下降法中权矢量附近随机变化的，其均值等于最陡下降法的权矢量。
LMS收敛条件：

在实际中，自相关矩阵的特征值计算很不方便，一般用迹来代替。


失调系数计算公式：

μ和输入功率加大都会增加失调系数，在保证收敛的情况下μ加大，会提高收敛速度。
失调系数M刻画了LMS算法最终的收敛性能，失调系数越小，LMS算法越收敛于接近最优滤波器的性能；反之，失调系数越大，LMS算法最终的收敛结果与最优滤波器的性能差距越大。
最小二乘LS(Least Square)算法准则： 以误差的平方和最小作为最佳误差准则。
LS 的平方和减少了梯度随机性，使它能趋于最优滤波器，故 LS 算法性能要优于LMS算法。
递推最小二乘算法RLS(Recursive Least-Squares)。
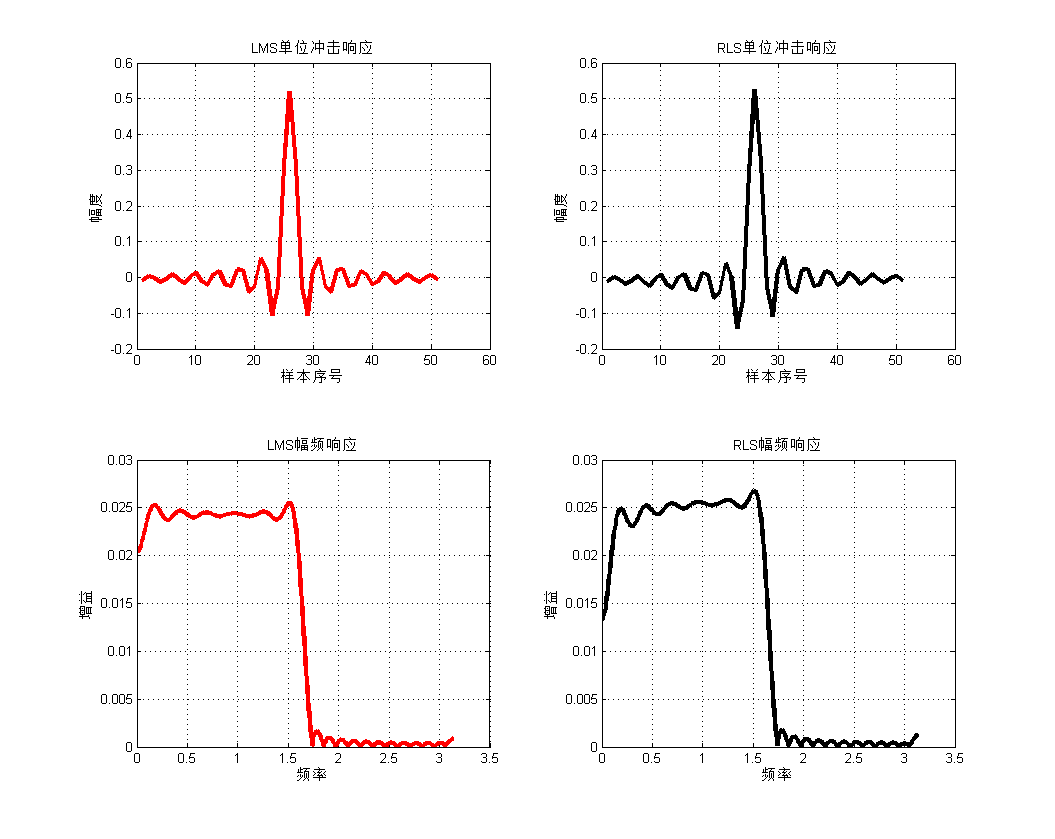
RLS 算法的收敛速率比 LMS算法快一个数量级；RLS 算法随着迭代趋于无限，其失调量收敛零；RLS 比LMS 有更好的性能，但性能的提高是以计算复杂性的增加为代价的。

---

总结

以上就是自适应数字滤波器的所有内容了，本文参考的课本是丁玉美数字信号处理-时域离散随机信号处理。