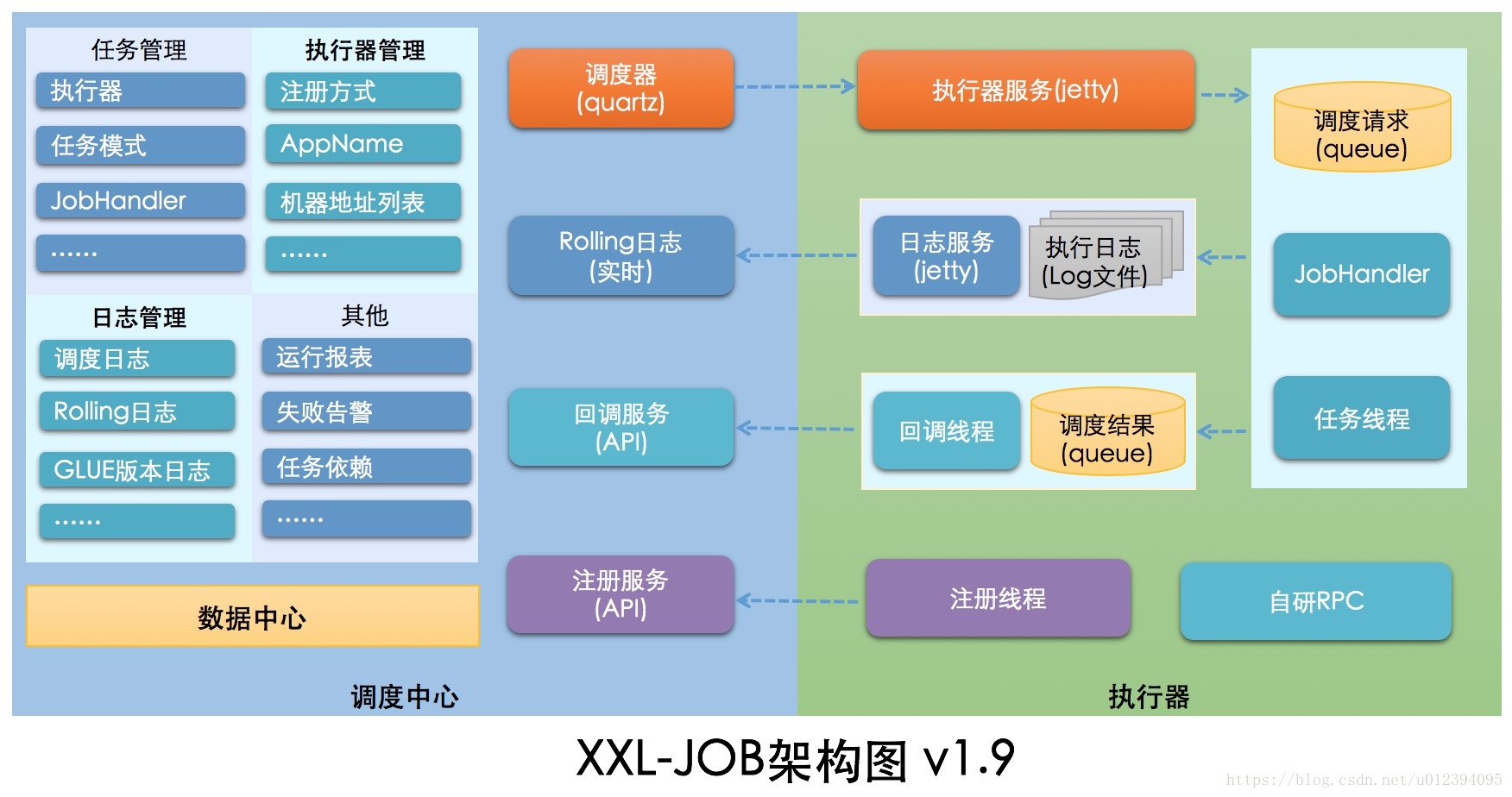
我要讲的几种方法
- 绪论
- 自适应滤波的基本原理
- 自适应滤波算法
- 自适应滤波算法种类
- 最小均方误差算法(LMS)
- 递推最小二乘算法(RLS)
- 变换域自适应滤波算法
- 仿射投影算法
- 其他
- 自适应滤波算法性能评价
- 自适应滤波的Matlab仿真
- 正弦信号加噪的LMS自适应滤波
- 代码
- 结果
- 音频信号Rolling in the Deep的LMS自适应滤波
- 音频资源
- 代码
- 结果及分析
- 其他
- 参考文献
绪论
- 自适应滤波是近30年以来发展起来的关于信号处理技术的方法。它是在维纳滤波、Kalman滤波等线性滤波基础上发展起来的一种最佳滤波方法。由于它具有更强的适应性和更优的滤波性能,从而在工程实际中,尤其在信息处理技术中得到了广泛的应用。
- 维纳滤波器等滤波器设计方法都是建立在信号特征先验知识基础上的。遗憾的是,在实际应用中常常无法得到信号特征先验知识,在这种情况下,自适应滤波器能够得到比较好的滤波性能。当输入信号的统计特性未知,或者输入信号的统计特性变化时,自适应滤波器能够自动地迭代调节自身的滤波器参数,以满足某种准则的要求,从而实现最优滤波。
- 自适应滤波的研究对象是具有不确定的系统或信息过程。这里的“不确定性”是指所研究的处理信息过程及其环境的数学模型不是完全确定的。其中包含一些未知因素和随机因素。
- 自适应滤波一般包括3个模块:滤波结构、性能判据和自适应算法。其中,自适应滤波算法的研究是自适应信号处理中最为活跃的研究课题之一,包括线性自适应算法和非线性自适应算法。非线性自适应算法具有更强的信号处理能力,但计算比较复杂,实际应用最多的仍然是线性自适应算法。
自适应滤波的基本原理

自适应滤波算法
自适应滤波算法种类
最小均方误差算法(LMS)
- 由Widrow和Hoff提出的最小均方误差(LMS)算法,因其具有计算量小、易于实现等优点而在实践中被广泛采用。
- 迭代公式如下:
e ( n ) = d ( n ) − X ⃗ T ( n ) W ⃗ ( n ) W ⃗ ( n + 1 ) = W ⃗ ( n ) + 2 u e ( n ) X ( n ) e(n) =d(n)-\vec{X}^T(n)\vec{W}(n)\\ \vec{W}(n+1)=\vec{W}(n)+2ue(n)X(n) e(n)=d(n)−XT(n)W(n)W(n+1)=W(n)+2ue(n)X(n)其中 u 是步长因子,LMS算法的收敛条件是 0 < u < 1 / λ m a x 0<u<1/\lambda_{max} 0<u<1/λmax, λ m a x \lambda_{max} λmax是输入信号自相关矩阵的最大特征值。 - 初始收敛速度、时变系统跟踪能力及稳态失调是衡量自适应滤波算法优劣的三个最重要的技术指标。由于主输入端不可避免地存在干扰噪声,自适应滤波算法将产生参数失调噪声。干扰噪声v(n)越大,则引起的失调噪声就越大。减小步长因子u可减小自适应滤波算法的稳态失调噪声,提高算法的收敛精度。然而步长因子u的减小将降低算法的收敛速度和跟踪速度。因此,固定步长的自适应滤波算法在收敛速度、时变系统跟踪速度与收敛精度方面对算法调整步长因子u的要求是相互矛盾的。为了克服这一矛盾,人们提出了许多变步长自适应滤波算法。R.D.Gitlin曾提出了一种变步长自适应滤波算法。其步长因子u(n)随迭代次数的增加而逐渐减小。Yasukawa提出了使步长因子u正比于误差信号e(n)的大小。而Gitlin等提出了一种时间平均估值梯度的自适应滤波算法。
- 变步长自适应滤波算法的步长调整原则是在初始收敛阶段或未知系统参数发生变化时,步长应比较大,以便有较快的收敛速度和对时变系统的跟踪速度;而在算法收敛后,不管主输入端干扰信号v(n)有多大,都应保持很小的调整步长以达到很小的稳态失调噪声。根据这一步长调整原则,有Sigmoid函数变步长LMS算法(SVSLMS),其变步长u是e(n)的Sigmoid函数:
u ( n ) = β ( 1 1 + e − α ∣ e ( n ) ∣ ) u(n)=\beta(\frac{1}{1+e^{-\alpha|e(n)|}}) u(n)=β(1+e−α∣e(n)∣1)该算法能同时获得较快的收敛速度、跟踪速度和较小的稳态误差。然而,该Sigmoid函数过于复杂,且在误差e(n)接近零处变化太大。不具有缓慢变化的特性,使得SVSLMS算法在自适应稳态阶段仍有较大的步长变化,这是该算法的不足。
递推最小二乘算法(RLS)
- LMS算法的优点是结构简单,鲁棒性强,其缺点是收敛速度慢。
- 基于最小二乘准则,RLS算法决定自适应滤波器的权系数向量W(n)使估计误差的加权平方和 J ( n ) = ∑ i = 0 n λ n − i ⋅ ∣ e ( i ) ∣ 2 J(n)=∑_{i=0}^nλ^{n-i}·|e(i)|^2 J(n)=i=0∑nλn−i⋅∣e(i)∣2最小。
- RLS算法对输入信号的自相关矩阵 R x x ( n ) R_{xx}(n) Rxx(n)的逆进行递推估计更新,收敛速度快,其收敛性能与输入信号的频谱特性无关。
- 推导与上面有一定的相似性,定义加权自相关: R x x ( n ) = E [ λ n − i X ⃗ X ⃗ T ] R_{xx}(n)=E[\lambda^{n-i}\vec{X}\vec{X}^T] Rxx(n)=E[λn−iXXT]可以得出RLS算法的基本关系:
W ⃗ ( n ) = W ⃗ ( n − 1 ) + k ( n ) e ( n − 1 ) \vec{W}(n)=\vec{W}(n-1)+k(n)e(n-1) W(n)=W(n−1)+k(n)e(n−1)
其中 k ( n ) = P ( n − 1 ) X ⃗ ( n ) λ + X ⃗ T ( n ) P ( n − 1 ) X ⃗ ( n ) , P ( n − 1 ) = R x x − 1 ( n ) k(n)=\frac{P(n-1)\vec{X}(n)}{\lambda+\vec{X}^T(n)P(n-1)\vec{X}(n)},P(n-1)=R^{-1}_{xx}(n) k(n)=λ+XT(n)P(n−1)X(n)P(n−1)X(n),P(n−1)=Rxx−1(n)
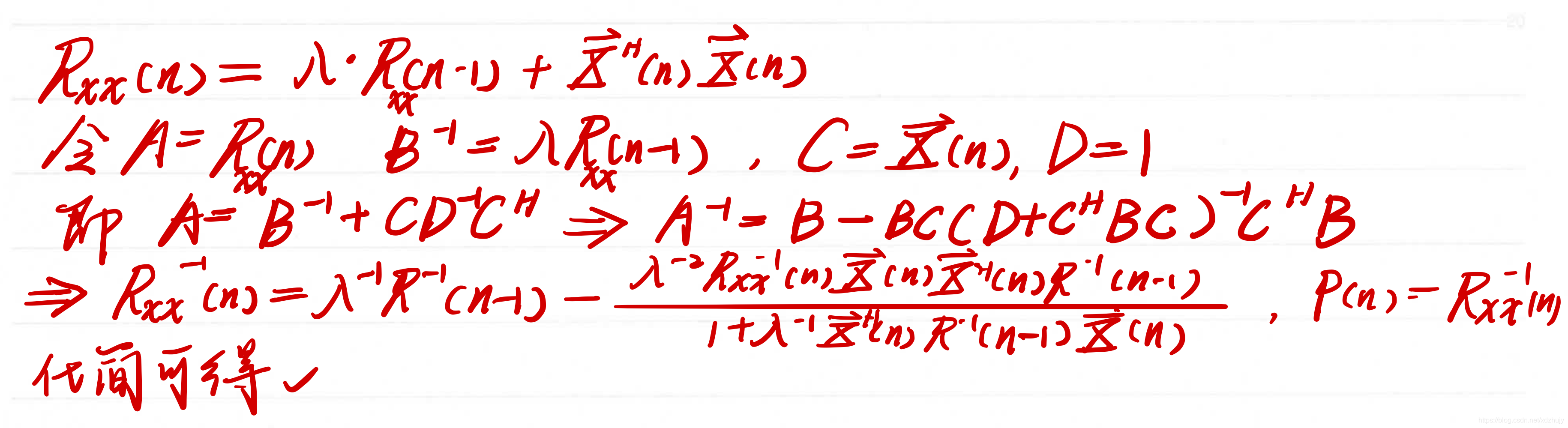
- 但是,RLS算法的计算复杂度很高,所需的存储量极大,不利于适时实现;倘若被估计的自相关矩阵 R x x ( n ) R_{xx}(n) Rxx(n)的逆失去了正定特性,这还将引起算法发散。为了降低RLS算法的计算复杂度,并保留RLS算法收敛速度快的特点,产生了许多改进的RLS算法。如快速RLS(Fast RLS)算法,快速递推最小二乘格型(Fast Recursive Least Squares Lattice)算法等。这些算法的计算复杂度低于RLS算法,但它们都存在数值稳定性问题。
- 改进的RLS算法着重于用格型滤波器的RLS算法,快速RLS算法就是在RLS格型算法基础上得到的。格型滤波器与直接形式的FIR滤波器可以通过滤波器系数转换相互实现。格型参数称为反射系数,直接形式的FIR滤波器长度是固定的,一旦长度改变则会导致一组新的滤波器系数,而新的滤波器系数与旧的滤波器系数是完全不同的。而格型滤波器是次序递推的,因此,它的级数的改变并不影响其它级的反射系数,这是格型滤波器的一大优点。RLS格型滤波器算法就是将最小二乘准则用于求解最佳前向预测器系数、最佳后向预测器系数,进行时间更新、阶次更新及联合过程估计。格型RLS算法的收敛速度基本上与常规RLS算法的收敛速度相同,因为二者都是在最小二乘的意义下求最佳。但格型RLS算法的计算复杂度高于常规RLS算法。格型RLS算法的数字精度比常规RLS算法的精度高,对舍入误差的不敏感性甚至优于LMS算法。
变换域自适应滤波算法
- 对于强相关的信号,LMS算法的收敛性能降低,这是由于LMS算法的收敛性能依赖于输入信号自相关矩阵的特征值发散程度。输入信号自相关矩阵的特征值发散程度越小,LMS算法的收敛性能越好。经过研究发现,对输入信号作某些正交变换后,输入信号自相关矩阵的特征值发散程度会变小。于是,Dentino等1979年首先提出了变换域自适应滤波的概念,其基本思想是把时域信号转变为变换域信号,在变换域中采用自适应算法。Narayan等对变换域自适应滤波算法作了全面的总结。
- 变换域自适应滤波算法的一般步骤是:
- 变换矩阵N*N的T矩阵,常用的正交变换有离散余弦变换(DCT)、离散傅立叶变换(DTFT)、离散Hartly变换及沃尔什—哈达玛(Walsh—Hadamard)变换等。变换后的信号为: X ′ = T ∗ X X^{'}=T*X X′=T∗X
- 变换域的递推公式: W ( n + 1 ) = W ( n ) + 2 u e ( n ) P − 1 ( n ) X ( n ) W(n+1)=W(n)+2ue(n) P^{-1} (n)X(n) W(n+1)=W(n)+2ue(n)P−1(n)X(n) P ( n ) = d i a g [ P ( n , 0 ) , P ( n , 1 ) , … , P ( n , N − 1 ) ] P(n)=diag[P(n,0),P(n,1),…,P(n,N-1)] P(n)=diag[P(n,0),P(n,1),…,P(n,N−1)] P ( n , l ) = β P ( n − 1 , l ) + ( 1 − β ) X T ( n , l ) ⋅ X ( n , l ) , l = 0 , 1 … N − 1 P(n,l)=βP(n-1,l)+(1-β) X^T (n,l)·X(n,l) ,l=0,1…N-1 P(n,l)=βP(n−1,l)+(1−β)XT(n,l)⋅X(n,l),l=0,1…N−1若令 Λ 2 = P ( n ) Λ^2=P(n) Λ2=P(n),则权系数向量的迭代方程为:
W ( n + 1 ) = W ( n ) + 2 u e ( n ) Λ − 2 X ( n ) W(n+1)=W(n)+2ue(n)Λ^{-2} X(n) W(n+1)=W(n)+2ue(n)Λ−2X(n)
仿射投影算法
- 仿射投影算法最早由K, Ozeki和T. Umeda提出,它是能量归一化最小均方误差(NLMS)算法的推广。仿射投影算法的性能介于LMS算法和RLS算法之间,其计算复杂度比RLS算法低。能量归一化最小均方误差(NLMS)算法是LMS算法的一种改进算法,NLMS算法可以看作是一种时变步长因子的LMS算法。其收敛性能对输入信号的能量变化不敏感。
- 仿射投影算法是NLMS算法的多维推广,假定P为投影阶数,仿射投影算法中权系数向量的修正量由下述方程组的最小二范解决定: Y ( k ) = X T ( k ) [ W ( k − 1 ) + Δ W ( k − 1 ) ] Y(k)=X^T (k)[W(k-1)+\Delta W(k-1)] Y(k)=XT(k)[W(k−1)+ΔW(k−1)]其中: Y ( k ) = [ y ( k ) , y ( k − 1 ) , … , y ( k − p + 1 ) ] Y(k)=[y(k),y(k-1),…,y(k-p+1)] Y(k)=[y(k),y(k−1),…,y(k−p+1)] X ( k ) = [ x ( k ) , x ( k − 1 ) , … , x ( k − p + 1 ) ] X(k)=[x(k),x(k-1),…,x(k-p+1)] X(k)=[x(k),x(k−1),…,x(k−p+1)]
利用矩阵的广义逆可求得 Δ W ( k − 1 ) \Delta W(k-1) ΔW(k−1),因此,仿射投影算法可表示为:
e ( k ) = Y ( k ) − X T ( k ) W ( k − 1 ) e(k)=Y(k)-X^T (k)W(k-1) e(k)=Y(k)−XT(k)W(k−1) g ( k ) = [ X T ( k ) X ( k ) + δ l ] − 1 e ( k ) g(k)=[X^T (k)X(k)+δl]^{-1}e(k) g(k)=[XT(k)X(k)+δl]−1e(k) W ( k ) = W ( k − 1 ) + u Δ W ( k − 1 ) = W ( k − 1 ) + u X ( k ) g ( k ) W(k)=W(k-1)+u\Delta W(k-1)=W(k-1)+uX(k)g(k) W(k)=W(k−1)+uΔW(k−1)=W(k−1)+uX(k)g(k)
其他
- 共轭梯度算法
- 基于子带分解的自适应滤波算法
- 基于QR分解的自适应滤波算法
- 其他
其他不再具体说明。
自适应滤波算法性能评价
下面对各种类型的自适应滤波算法进行简单的总结分析。
- 变步长的自适应滤波算法虽然解决了收敛速度、时变系统跟踪速度与收敛精度方面对算法调整步长因子u的矛盾,但变步长中的其它参数的选取还需实验来确定,应用起来不太方便。
- 对RLS算法的各种改进,其目的均是保留RLS算法收敛速度快的特点而降低其计算复杂性。
- 变换域类算法亦是想通过做某些正交变换使输入信号自相关矩阵的特征值发散程度变小。提高收敛速度。
- 而仿射投影算法的性能介于LMS算法和RLS算法之间。
- 共轭梯度自适应滤波算法的提出是为了降低RLS类算法的杂性和克服某些快速RLS算法存在的数值稳定性问题。
- 信号的子带分解能降低输入信号的自相关矩阵的特征值发散程度,从而加快自适应滤波算法的收敛速度,同时便于并行处理,带来了一定的灵活性。
- 矩阵的QR分解具有良好的数值稳定性。
自适应滤波的Matlab仿真
正弦信号加噪的LMS自适应滤波
代码
clc,clear,close all;
g=100;
L=1024;%信号长度
k=128;%滤波器阶数
pp=zeros(g,L-k);
u=0.001;
for q=1:gt=1:L;a=1;s=a*sin(0.05*pi*t);figure(1);subplot(311);plot(s);title('信号s时域波形');xlabel('n');axis([0,L,-a-1,a+1]);xn=awgn(s,5); %信噪比5dB的WGNy=zeros(1,L);y(1:k)=xn(1:k);w=zeros(1,k);e=zeros(1,L);for i=(k+1):LXN=xn((i-k+1):(i));y(i)=w*XN';e(i)=s(i)-y(i);pp(i)=pp(i)+e(i);w=w+u*e(i)*XN;end
end
subplot(312)
plot(xn);
title('信号加高斯白噪声后的时域波形');
axis([0,L,-a-2,a+2]);
subplot(313)
plot(y);
axis([0,L,-a-1,a+1]);
title('LMS算法自适应滤波后的输出时域波形');
结果
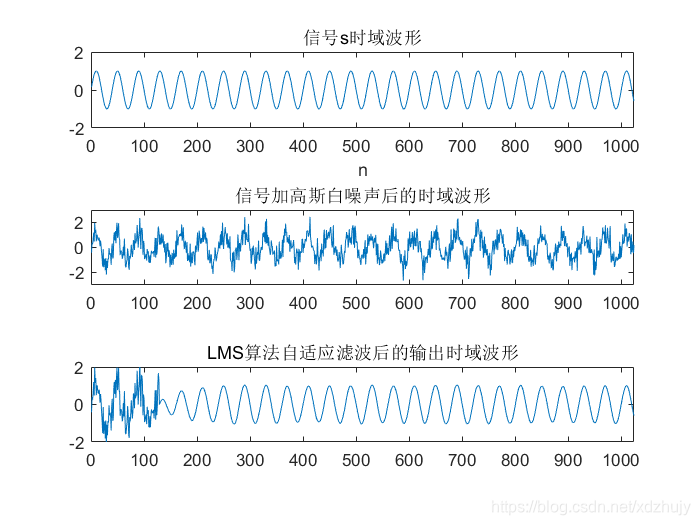
音频信号Rolling in the Deep的LMS自适应滤波
音频资源
已把音频放在了 https://pan.baidu.com/s/1L5vXa60c0wEATx2LQVLp-Q
提取码:vs7o
代码
- LMSfilter.m
function [y,W,e]=LMSfilter(xn,d,L,mu)
% 输入参数:
% xn 输入的信号序列 (列向量)
% d 所期望的响应序列 (列向量)
% L 滤波器的阶数 (标量)
% mu 收敛因子(步长) (标量) 要求0<mu<xn的相关矩阵最大特征值的倒数
% 输出参数:
% W 滤波器的权值矩阵 (矩阵)
% 大小为M x t,
% e 误差序列(t x 1) (列向量)
% y 实际输出序列 (列向量)
t = length(xn);
e = zeros(t,1); % 误差序列,en(k)表示第k次迭代时预期输出与实际输入的误差
W = zeros(L,t); % 每一行代表一个加权参量,每一列代表-次迭代,初始为0
% 迭代计算
for k = L:t % 第k次迭代x = xn(k:-1:k-L+1); % 滤波器L个抽头的输入y = W(:,k-1).'*x; % 滤波器的输出e(k) = d(k)- y ; % 第k次迭代的误差W(:,k) = W(:,k-1) + 2*mu*e(k)*x; % 滤波器权值计算的迭代式
end
% 求最优时滤波器的输出序列 r如果没有yn返回参数可以不要下面的
y = inf * ones(size(xn)); % inf 是无穷大的意思
for k = L:length(xn)x = xn(k:-1:k-L+1);y(k) = W(:,end).'* x;%用最后得到的最佳估计得到输出
end
- main.m
clc;
clear all;
close all;%% 产生信号源
[X,Fs] = audioread('Rolling in the Deep.wav');%音频过长无法计算自相关
signal = X(:,1); %取出双通道中其中一个通道作为信号源signal
audiowrite('原始音频.wav',signal,Fs); %创建原始音频.wav
n = length(signal);
t=(0:n-1);
figure(1);
subplot(3,1,1);
plot(t,signal);grid;ylim([-2 2]);
ylabel('幅度');
xlabel('时间');
title('原始音频信号');%% 产生期望信号
dn = awgn(signal,10); %加入信噪比为10dB的高斯白噪声
noise=dn-signal;
audiowrite('含噪音频.wav',dn,Fs); %创建含噪音频
subplot(3,1,2);
plot(t,dn);grid;ylim([-2 2]);
ylabel('幅度');
xlabel('时间');
title('含噪音频信号');%% LMS滤波算法
M = 128; %滤波器阶数M
u = 0.0004; %滤波器的步长
[yLMS,W,eLMS] =LMSfilter(noise,dn,M,u);%% 绘制去噪后的语音信号
subplot(3,1,3);
plot(t,eLMS);grid;ylim([-2 2]);
ylabel('幅度');
xlabel('时间');
title('去噪后的音频信号');
audiowrite('去噪音频.wav',eLMS,Fs);%保存去除噪声的音频%%
e = signal-eLMS;%剩余噪声
figure(2);
subplot(2,1,1);
plot(t,e);grid;
ylabel('幅度');
xlabel('时间');
title('剩余的噪声');%% 一小段三个信号比较
subplot(2,1,2);
t=(1000000:1005000);
plot(t,eLMS(1000000:1005000,1 ),'r',t,e(1000000:1005000,1),'g',t,signal(1000000:1005000,1),'b');
axis([1000000,1005000,-1,1]);
ylabel('幅度');
xlabel('时间');
legend('去噪后的语音信号','剩余噪声','原始音频');
title('一小段三个信号比较');
结果及分析
- u=0.0004,SNR=10dB时:

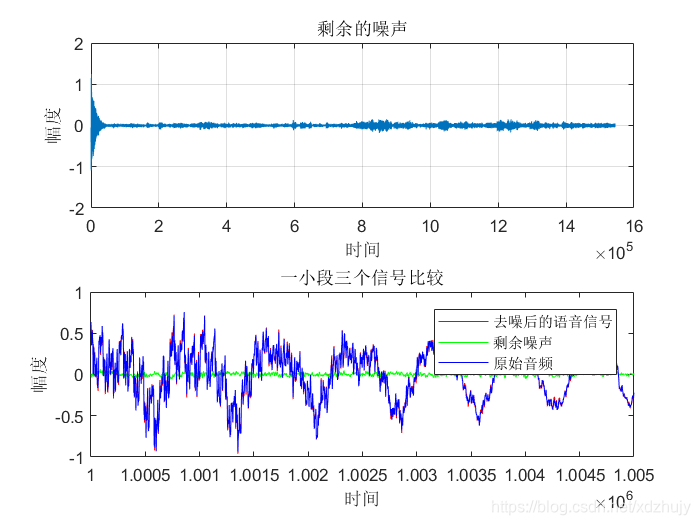
- u=0.0008,SNR=10dB时:
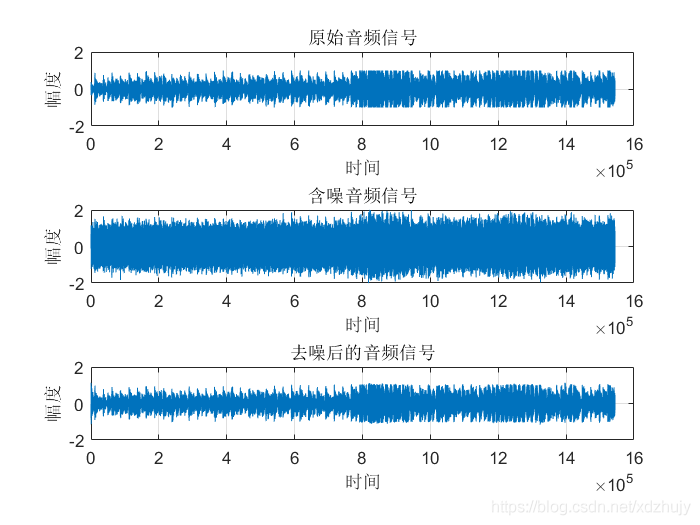
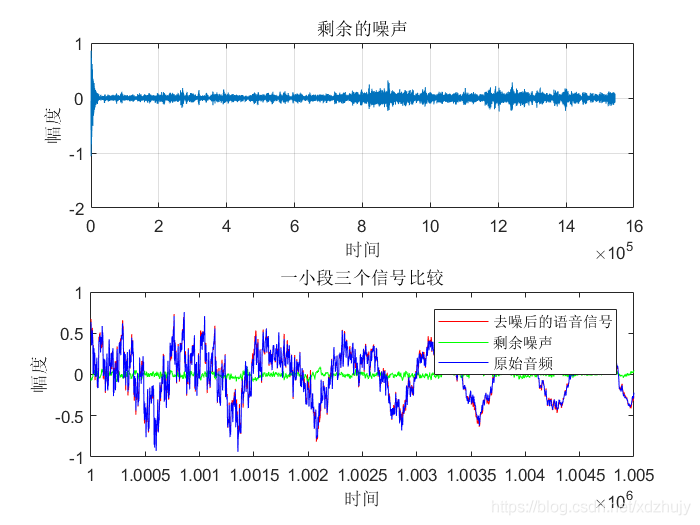
- u=0.0016,SNR=10dB时:
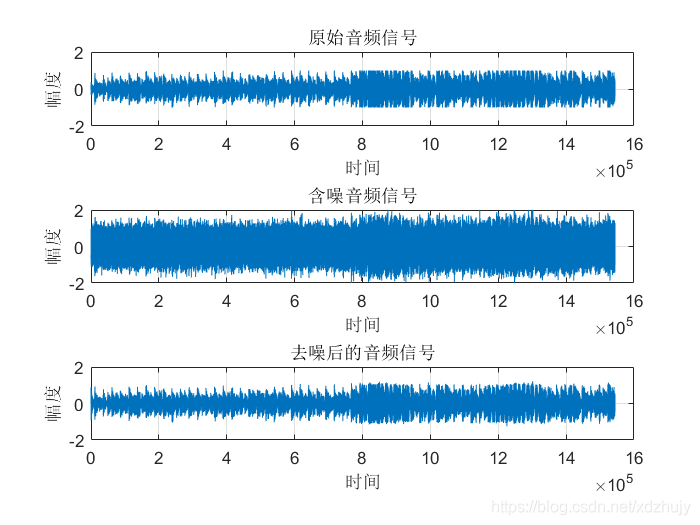
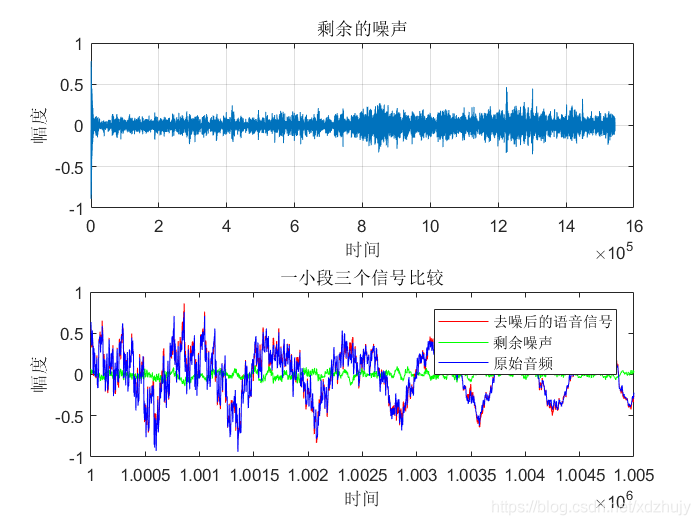
- u=0.0004,SNR=15dB时:
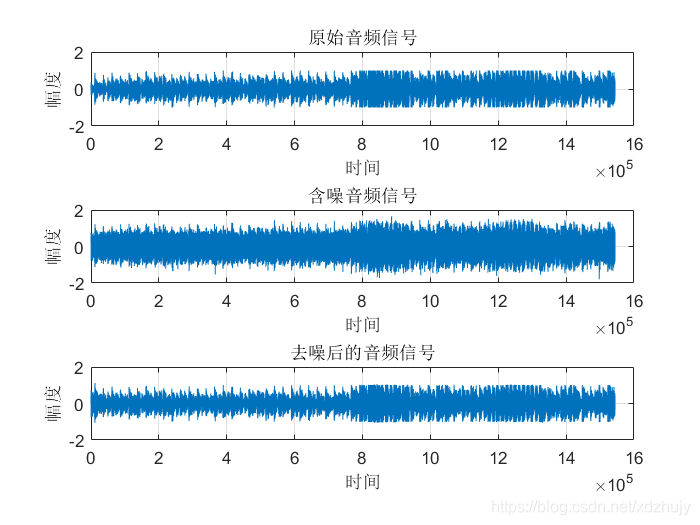
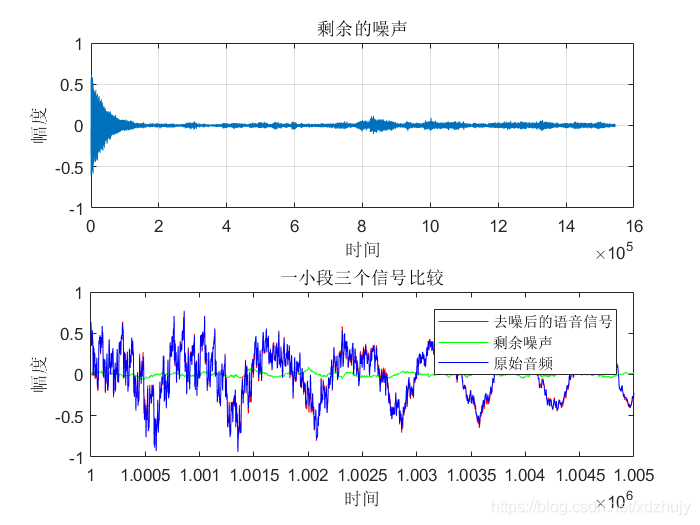
- 从图中可以看出虽然真实的音频信号中混杂了很强的噪声,甚至噪声淹没了真实的信号,但是通过我们的LMS自适应滤波器后,可以很好的恢复出真实信号。所以自适应滤波器具有良好的去噪性能。
- 通过改变步长u,我发现随步长++,收敛时间–。但是当u增加,音频信号越来越清晰。但是当步长超过某一值时,音频中又开始很有噪声产生,再接着增加步长u,甚至会把音频信号也滤去掉。所以若 μ 值取的过小,收敛速度就会过于缓慢,当u取的过大时,又会造成系统收敛的不稳定,导致发散。
- 提高信噪比会使收敛时间变长。
其他
- 图像处理中wiener2()函数用于对图像进行自适应除噪滤波,其可以估计每个像素的局部均值与方差,调用方式如下:
J=wiener2(I,[M,N],noise);
%表示M*N大小邻域局部图像均值与偏差,采用像素自适应滤波器对图像I滤波
参考文献
- https://wenku.baidu.com/view/457b0bc04028915f804dc241.html
- https://wenku.baidu.com/view/dadab78404a1b0717fd5ddb4.html
- https://blog.csdn.net/baidu_36161424/article/details/83244715
- https://blog.csdn.net/zlh_hhhh/article/details/89061839
- https://www.cnblogs.com/augustine0654/p/10041313.html
- 耿妍,张端金.自适应滤波算法综述[J].信息与电子工程,2008,6(4),315-320.
- 邹艳碧, 高鹰.自适应滤波算法综述[J].广州大学学报(自然科学版),2002,1(2),44-48.