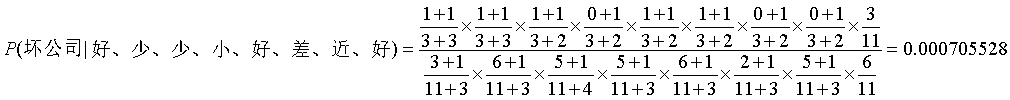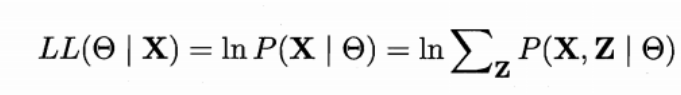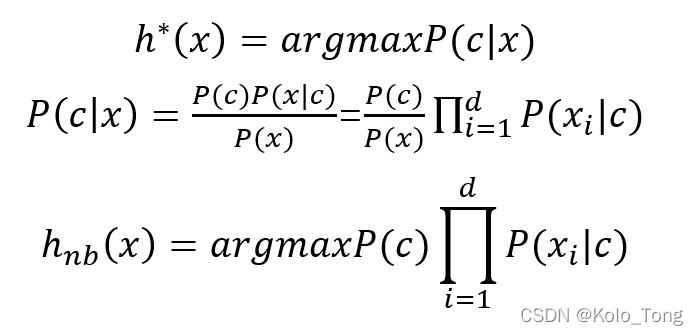目录
错误率与风险
朴素贝叶斯分类器
平滑:拉普拉斯修正
半朴素贝叶斯分类器
错误率与风险
书接上回,我们讲到最大后验概率,我们期望把概率最大时对应的属性,当做它最终的结果。我们自然也会思考,这样做准不准,我们的犯错率有多大?
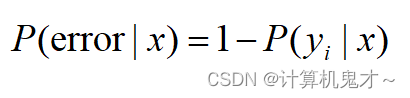
也就是说,在条件x的情况下,预测失误的概率(即犯错率)为1减去预测正确概率后的值。是不是有一种听君一席话,胜似一席话的感受?
那么,看懂了上述式子后,我们继续推进。不同的错误带来的损失不尽相同。比如说,如果我们把病人预测成健康的人,会导致他没能及时治疗,其损失肯定远大于把健康人预测成了病人。

显然,对每个样本x ,若 h 能最小化条件风险R(h(x)|x),则总体风险也将被最小化.这就产生了贝叶斯判定准则:为了使总体风险最小,只需在每个样本x上选择那个能使条件风险R(c|x)最小的类别,即 :
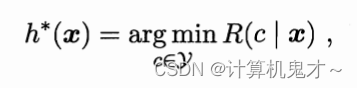
我们将h*称为贝叶斯分类器,与之对应的R(h*)称作贝叶斯风险,1-R(h*)则反映了分类器所能达到的最好性能。
更一般的,如果我们希望最小化分类错误率,即预测错误损失为1,预测成功损失为0,这样我们预测的类别,就又会变成算出最大后验概率时所对应的类别。
朴素贝叶斯分类器
讲解这方面知识,我觉得先上一个例子会好一些
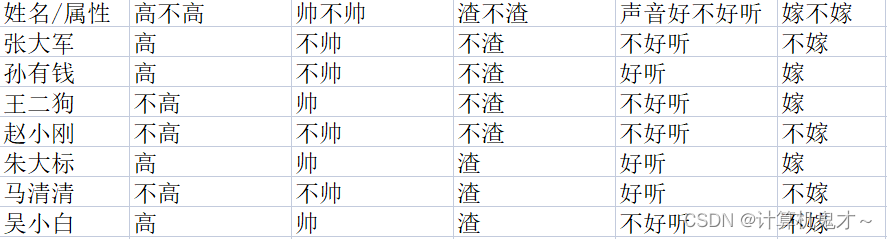
好啦,现在我们决定给人美心善的伍老师找对象啦,伍老师决定从身高、帅不帅、渣不渣、声音好不好听四个角度对前来相亲的男嘉宾进行考察,再决定嫁不嫁。前来相亲的男嘉宾的条件极其结果如下:
那么根据上面的结果(伍老师可没有养鱼啊,因为种种原因孙有钱、王二麻子和朱大标不能娶伍老师),此时,高、帅、不渣、声音不好听的小明前来相亲,请替伍老师判断,该不该嫁?
对于朴素贝叶斯分类器,它的思想是避开联合概率,而采用“属性条件独立性假设”。
什么意思?就是说每个属性独立的对分类的结果发生影响。结合例子也就是说这四个属性互不影响(比如说,这个男嘉宾高不高不影响他渣不渣),单独对伍老师嫁不嫁起作用(比如说,渣不渣和高不高单独对她嫁不嫁起作用)。
所以,我们有:
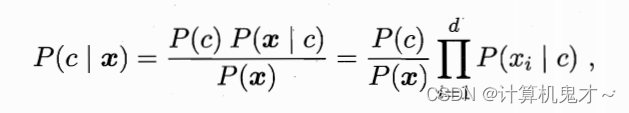
注意x 是一个向量哦
我们发现,分母P(x)是个固定的值,对于分类没有影响,所以基于贝叶斯判定准则,我们只需要求出:
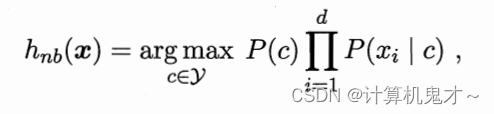
那么,现在的问题转化为,我们要算出嫁给高、帅、不渣、声音不好听的小明的概率,与不嫁给高、帅、不渣、声音不好听的小明的概率。把二者作比较,如果嫁的概率高于不嫁的概率,那么最终会选择嫁,反之则不嫁。

看得出来,朴素贝叶斯分类器能做很多有意义的判断,果然女生都是爱帅哥的,同时让我们恭喜男女嘉宾牵手成功!!
平滑:拉普拉斯修正
是不是觉得贝叶斯分类器很有意思?那么为了考察大家学的怎么样,小编请大家用朴素贝叶斯分类器的思想完成下面的题目:
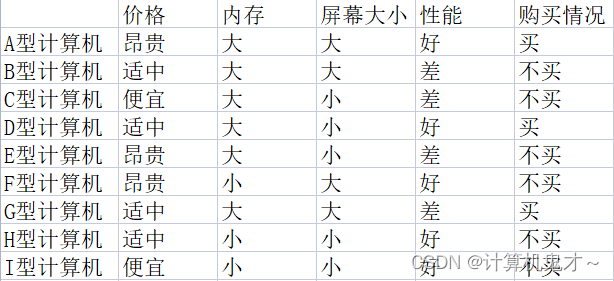
例题:伍老师最近读了小编的文章后,迷上了编程,今天我们要帮助伍老师挑选更合适的计算机,已知对于伍老师而言,计算机的特性与她买不买相机的部分对应关系如下:
那么,请用朴素分类器的思想判断,对于价格便宜、内存大、屏幕大、性能好的计算机,伍老师是买还是不买?
让小编来还原一下大家的思路:

倘若你完成到了这一步,那么恭喜你,整体的思路并没有错,错的是样本的数量太少了。我们来算一算,一共有多少种情况:价格有三种,性能有两种,内存有两种,屏幕大小有两种,一共是3×2×2×2=24种,但是样本只有9个,且在这些样本中,只要是便宜的,伍老师都不打算买,而机器又没有我们这么聪明,它很笨,不知道变通,要是既便宜又各方面都不错的话,小编肯定是买了。所以我们为了让机器学会“变通”,其“变通”方法就是“平滑”操作,我们常用“拉普拉斯修正法”
拉普拉斯修正法的思想如下:

如果你感觉不好理解公式,那么小编把这个题通过拉普拉斯修正后重新做一遍,大家稍微理解一下:

有的同学会吐槽,闹了半天,不照样不会买吗,那用拉普拉斯修正有什么用,伍老师不照样还是那个富婆吗?小了,我只能说你格局太小了,虽然在本题中确实如此,但是拉普拉斯修正为我们提供了一种“变通”的良好思路,我们要学会通过现象、通过题目去看问题的本质,再去寻找更加合适的方法,我想,这就是数学的魅力所在吧!
半朴素贝叶斯分类器
为了让大家更好理解,我仍然先上一个例子
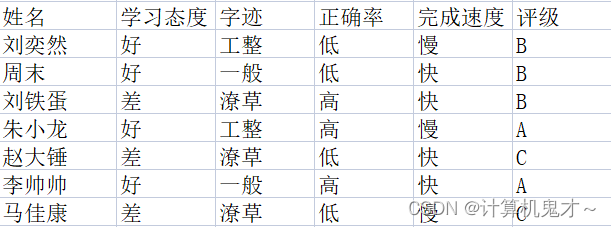
引例:刚刚伍老师去买了计算机,买计算机需要时间,导致伍老师没时间批改作业了,那么,为了让伍老师买计算机时不分心,接下来由我们替伍老师改作业。我们决定从平时学习态度、作业字迹、正确率以及完成速度来给同学们的作业评级。(一般作业的字迹、正确率、完成速度和平时的学习态度有相互依赖关系!)
改到下一份作业时,该学生的学习态度很好,字迹一般,正确率低且完成速度慢,聪明的你应该给他的作业评什么等级?
震惊!这四个属性之间有相互依赖关系,岂不是说不能用朴素贝叶斯分类器了吗?那该怎么办?
是的朴素贝叶斯分类器在平时很难成立,因为属性条件独立假设并不是那么容易实现。所以热爱学习的我们要来学习另一种更厉害的分类器:半朴素贝叶斯分类器!
半朴素贝叶斯分类器的基本想法是适当考虑一部分属性间的相互依赖信息,从而既不需进行完全联合概率计算,又不至于彻底忽略了比较强的属性依赖关系 。“独依赖估计”是半朴素贝叶斯分类器最常用的一种策略。顾名思议,所谓“独依赖”就是假设每个属性在类别之外最多仅依赖于一个其他属性。就比如说,举个例子:字迹、正确率以及完成速度都仅依赖于学习态度。
有下面这个公式,大家应该能够理解:
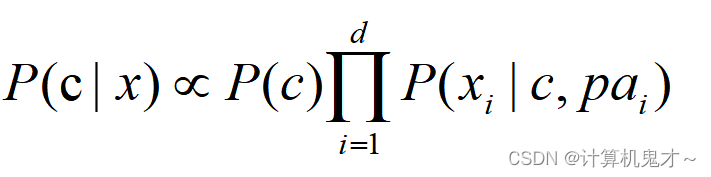
所以问题的关键转换为如何求出这个被依赖的属性!
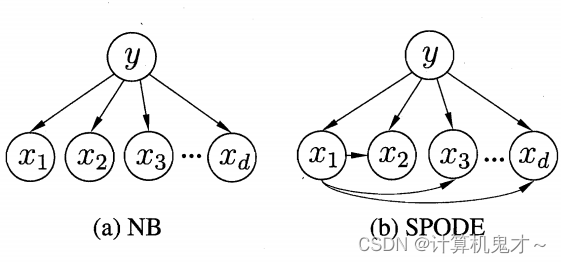
对于所有属性都依赖于同一个属性的情况,我们会称该属性为“超父属性”,比如例题中假如字迹、正确率以及完成速度都仅依赖于学习态度,那么超父属性就为“学习态度 ”,下图中,a图为朴素贝叶斯的依赖情况,b图为超父独依赖的依赖情况。
至于TAN算法,有点过于复杂了,感兴趣的同学们可以自己到别的网站中自己学一下。
咳咳,扯远了,学到这里,相信大家已经对贝叶斯分类器有一定了解了。不过,机器学习算法课还没有结束哦。欲知后事如何,请您点赞加关注,您的点赞加关注是小编写下去最大的动力!