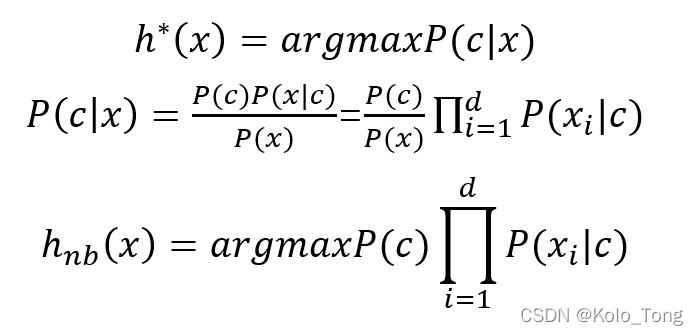贝叶斯分类器(Bayes Classifier)

一、贝叶斯定理

1、背景：

贝叶斯定理也称贝叶斯推理，早在18世纪，英国学者贝叶斯(1702～1763)曾提出
引用：百度百科

贝叶斯定理是关于随机事件A和B的条件概率（或边缘概率）的一则定理。其中P(A|B)是在B发生的情况下A发生的可能性。
贝叶斯定理计算条件概率的公式用来解决如下一类问题：

	假设：H[1],H[2]…,H[n]互斥且构成一个完全事件已知它们的概率P(H[i]),i=1,2,…,n,现观察到某事件A与H[1],H[2]…,H[n]相伴随机出现且已知条件概率P(A|H[i])，求P(H[i]|A)

1.2、贝叶斯公式：
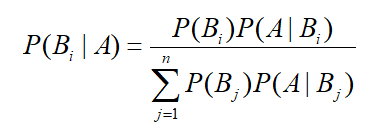
在这里插入图片描述

公式描述中：P(Bi)为事件Bi发生的概率，事件Bi在已经发生的条件下A的概率为P(A|B)，事件A发生条件下事件Bi的概率为P(Bi|A)

1.2、贝叶斯概率的定义与贝叶斯公式：

假设，A和B是两个事件公式如下：

A发生的概率记作：P(A)
B发生的概率记作：P(B)
A和B同时发生的概率记作：P(AB)
条件概率P(B|A)为：
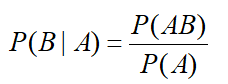
由上图公式可得：P(AB)=P(B|A)P(A)

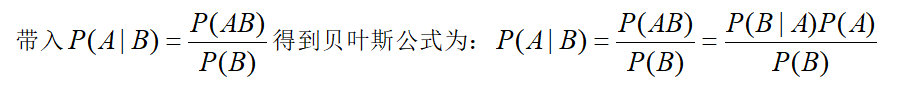
1.3、贝叶斯公式的应用：

1.3.1，双色球盒问题：

 假设有5个盒子，其中各自装了两个球，球总共有两种颜色，具体如下已知样本空间Ω={（红、红），（红、白），（白、红），（白、白），（白、白）}问题：事件A为{盒子中至少有一个红球}事件B为{盒子中至少有一个白球}盒子中至少有一个红求的条件下，至少有一个白球的概率解：P(A)={（红、红），（红、白），（白、红）}P(B)={（白、白），（红、白），（白、红），（白、白）}	可盒子中至少有一个红求的条件下，至少有一个白球的概率=P(B|A)求得概率为2/3，如下图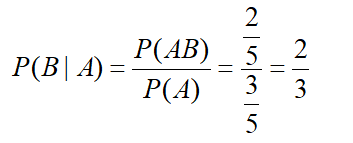

在这里插入图片描述

 实验中样本点的总数为n，事件A所包含的样本点数为m（m>0）AB所包含的样本点数为k，则可推出：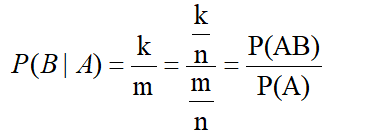

在这里插入图片描述

1.4、朴素贝叶斯分类的应用：

1.4.2，优缺点：
（1）算法逻辑简单,易于实现（算法思路很简单，只要使用贝叶斯公式转化即可！）
（2）分类过程中时空开销小（假设特征相互独立，只会涉及到二维存储）
1.4.2，bayes分类一个好公司问题，数据集如下：
1.4.3，构建数学模型(数学处理过程)：

①问题：
A公司满足Ω={福利少、加班少、工资中、压力小、发展前景好、氛围好、位置近、环境好}求，该公司是否是好公司？
解：
公式A如下

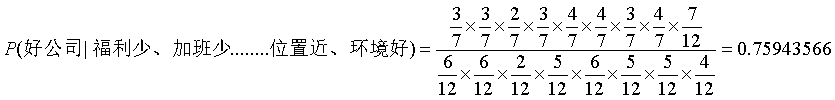
公式B如下

②拉普拉斯平滑系数：
根据公式p(工资中|坏公司)=0，肯定不符合真实情况，所以需要“拉普拉斯平滑系数”：当我们在使用朴素贝叶斯算法去解决分类问题时，在训练集上进行训练时我们可以发现有可能出现某些特征的概率P为0的情况，无论是在全文检索中某个字出现的概率，还是在垃圾邮件分类中，这种情况明显是不太合理的，不能因为一个事件没有观察到就武断的认为该事件的概率是0，拉普拉斯的理论支撑而拉布拉斯平滑处理正是处理这种情况下应运而生的。
③拉普拉斯平滑系数化：

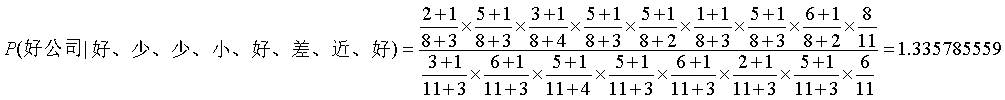
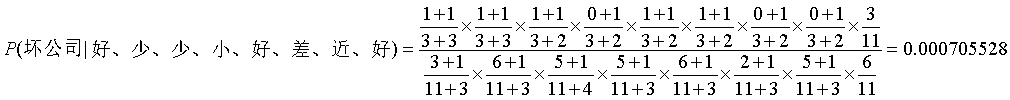
1.4.4，代码实现Naive Bayes 分类：

# -*- coding: utf-8 -*-
from numpy import *
from functools import reduceadClass = 1def loadDataSet():"""加载数据集合及其对应的分类"""# 福利	加班	工资	工作压力	发展前景	公司氛围	公司位置	环境wordsList = [['福利少', '加班多', '工资少', '压力大', '发展前景差', '氛围中', '位置中', '环境差'],['福利好', '加班少', '工资多', '压力小', '发展前景好', '氛围好', '位置近', '环境好'],['福利好', '加班中', '工资中', '压力中', '发展前景好', '氛围好', '位置近', '环境好'],['福利中', '加班少', '工资少', '压力小', '发展前景中', '氛围好', '位置近', '环境好'],['福利少', '加班中', '工资少', '压力中', '发展前景差', '氛围中', '位置远', '环境中'],['福利中', '加班多', '工资多', '压力大', '发展前景中', '氛围好', '位置远', '环境中'],['福利少', '加班多', '工资中', '压力大', '发展前景差', '氛围中', '位置中', '环境差'],['福利中', '加班少', '工资少', '压力小', '发展前景好', '氛围中', '位置近', '环境好'],['福利中', '加班多', '工资多', '压力大', '发展前景中', '氛围好', '位置远', '环境中'],['福利少', '加班少', '工资多', '压力小', '发展前景好', '氛围中', '位置中', '环境好'],['福利少', '加班少', '工资少', '压力小', '发展前景好', '氛围差', '位置近', '环境好'],['福利少', '加班少', '工资少', '压力大', '发展前景好', '氛围差', '位置中', '环境差'],]# 1 是, 0 否classVec = [0,1, 1, 0,0, 1, 1, 0, 1, 1,1,0]return wordsList, classVec# python中的& | 是位运算符   and or是逻辑运算符 当and的运算结果为true时候返回的并不是true而是运算结果最后一位变量的值
# 当and返回的结果是false时候，如果A AND B 返回的是第一个false的值，如果a为false 则返回a，如果a不是false，那么返回b
# 如果a or b 为true时候，返回的是第一个真的变量的值，如果a,b都为真时候那么返回a 如果a为假b为真那么返回b
# a & b a和b为两个set,返回结果取a和b的交集  a|b a和b为两个set,返回结果为两个集合的不重复并集def doc2VecList(docList):# 从第一个和第二个集合开始进行并集操作，最后返回一个不重复的并集# a = list(reduce(lambda x, y: set(x) | set(y), docList))a =['环境好', '氛围中', '压力大', '压力小', '工资少', '氛围好', '加班多', '福利少', '发展前景差', '福利好', '环境差', '加班少', '加班中', '位置远', '工资中', '位置中', '氛围差', '环境中', '压力中', '发展前景中', '工资多', '位置近', '福利中', '发展前景好']return adef words2Vec(vecList, inputWords):"""把单子转化为词向量"""# 转化成以一维数组resultVec = [0] * len(vecList)for word in inputWords:if word in vecList:# 在单词出现的位置上的计数加1resultVec[vecList.index(word)] += 1else:print('没有发现此单词')return array(resultVec)#trainMat, classVec
def trainNB(trainMatrix, trainClass):"""计算，生成每个词对于类别上的概率"""# 类别行数numTrainClass = len(trainClass)# 列数numWords = len(trainMatrix[0])# 全部都初始化为1， 防止出现概率为0的情况出现# 见于韩家炜的数据挖掘概念与技术上的讲解，避免出现概率为0的状况，影响计算，因为在数量很大的情况下，在分子和分母同时+1的情况不会# 影响主要的数据p0Num = ones(numWords)p1Num = ones(numWords)# 相应的单词初始化为1# 为了分子分母同时都加上某个数λp0Words = 1.0p1Words = 1.0# 统计每个分类的词的总数# 训练数据集的行数作为遍历的条件，从1开始# 如果当前类别为1，那么p1Num会加上当前单词矩阵行数据，依次遍历# 如果当前类别为0，那么p0Num会加上当前单词矩阵行数据，依次遍历# 同时统计当前类别下单词的个数和p1Words和p0Wordsfor i in range(numTrainClass):if trainClass[i] == 1:# 数组在对应的位置上相加p1Num += trainMatrix[i]p1Words += sum(trainMatrix[i])# print("i=",i,",p1Words=",p1Words,",trainMatrix[i]=",trainMatrix[i])else:p0Num += trainMatrix[i]p0Words += sum(trainMatrix[i])# print("i=",i,",p1Num=",p1Num,",trainMatrix[i]=",trainMatrix[i])print("i=",i,',p0Num=',p0Num,",p0Words=",p0Words,",trainMatrix[i]=",trainMatrix[i])# 计算每种类型里面， 每个单词出现的概率# 朴素贝叶斯分类中，y=x是单调递增函数，y=ln(x)也是单调的递增的# 如果x1>x2 那么ln(x1)>ln(x2)# 在计算过程中，由于概率的值较小，所以我们就取对数进行比较，根据对数的特性# ln(MN) = ln(M)+ln(N)# ln(M/N) = ln(M)-ln(N)# ln(M**n)= nln(M)# 注：其中ln可替换为log的任意对数底print("p0Num==",p0Num)print("p0Num / p0Words===",p0Num / p0Words)p0Vec = log(p0Num / p0Words)p1Vec = log(p1Num / p1Words)# 计算在类别中1出现的概率，0出现的概率可通过1-p得到pClass1 = sum(trainClass) / float(numTrainClass)return p0Vec, p1Vec, pClass1def classifyNB(testVec, p0Vec, p1Vec, pClass1):# 朴素贝叶斯分类, max(p0， p1)作为推断的分类# y=x 是单调递增的， y=ln(x)也是单调递增的。 ， 如果x1 > x2, 那么ln(x1) > ln(x2)# 因为概率的值太小了，所以我们可以取ln， 根据对数特性ln(ab) = lna + lnb， 可以简化计算# sum是numpy的函数，testVec是一个数组向量，p1Vec是一个1的概率向量，通过矩阵之间的乘机# 获得p(X1|Yj)*p(X2|Yj)*...*p(Xn|Yj)*p(Yj)# 其中pClass1即为p(Yj)# 此处计算出的p1是用对数表示，按照上面所说的，对数也是单调的，而贝叶斯分类主要是通过比较概率# 出现的大小，不需要确切的概率数据，因此下述表述完全正确# p1 = sum(testVec * p1Vec) + log(pClass1)# p0 = sum(testVec * p0Vec) + log(1 - pClass1)p1 = sum(testVec * p1Vec) + log(pClass1)p0 = sum(testVec * p0Vec) + log(1 - pClass1)print("p1=", p1, ",p0=", p1)if p0 > p1:return 0return 1def printClass(words, testClass):if testClass == adClass:print(words, '推测为：好公司')else:print(words, '推测为：坏公司')def tNB():# 从训练数据集中提取出属性矩阵和分类数据docList, classVec = loadDataSet()allWordsVec = doc2VecList(docList) #去重print("allWordsVec=",allWordsVec)# 构建词向量矩阵# 计算docList数据集中每一行每个单词出现的次数，其中返回的trainMat是一个数组的数组print("docList：", docList)trainMat = list(map(lambda x: words2Vec(allWordsVec, x), docList))print("trainMat：",trainMat)# 训练计算每个词在分类上的概率, p0V:每个单词在非分类出现的概率， p1V:每个单词在是分类出现的概率# 其中概率是以ln进行计算的# pClass1为类别中是1的概率p0V, p1V, pClass1 = trainNB(trainMat, classVec)# 测试数据集print("p0V:", p0V)print("p1V:", p1V)print("pClass1:", pClass1)#福利	加班	工资	工作压力	发展前景	公司氛围	公司位置	环境# testWords = ['福利少', '加班多', '工资多', '压力大', '发展前景差', '氛围中', '位置中', '环境差']testWords = ['福利少', '加班多', '工资多', '压力大', '发展前景差', '氛围中', '位置中', '环境差']# testWords = ['公司', '聚餐', '讨论', '贝叶斯']# 转换成单词向量，32个单词构成的数组，如果此单词在数组中，数组的项值置1testVec = words2Vec(allWordsVec, testWords)print("testWords=",testWords,",testVec=",testVec)# 通过将单词向量testVec代入，根据贝叶斯公式，比较各个类别的后验概率，判断当前数据的分类情况testClass = classifyNB(testVec, p0V, p1V, pClass1)# 打印出测试结果printClass(testWords, testClass)# 福利	加班	工资	工作压力	发展前景	公司氛围	公司位置	环境# testWords = ['福利少', '加班少', '工资多', '压力小', '发展前景好', '氛围好', '位置近', '环境好']testWords = ['福利少', '加班少', '工资中', '压力小', '发展前景好', '氛围好', '位置近', '环境好']# 转换成单词向量，32个单词构成的数组，如果此单词在数组中，数组的项值置1testVec = words2Vec(allWordsVec, testWords)# 通过将单词向量testVec代入，根据贝叶斯公式，比较各个类别的后验概率，判断当前数据的分类情况testClass = classifyNB(testVec, p0V, p1V, pClass1)# 打印出测试结果printClass(testWords, testClass)if __name__ == '__main__':tNB()# x# print(len(a))# print(log(4,2))# print(words2Vec(['高', '差', '少', '中', '好', '近', '小', '远', '多'],['少', '多', '少', '高', '差', '中', '中', '差']))

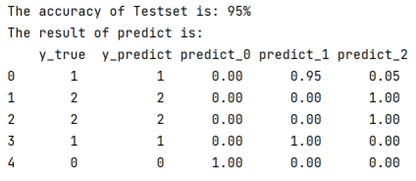
‘’‘输出结果’‘’
['福利少', '加班多', '工资多', '压力大', '发展前景差', '氛围中', '位置中', '环境差'] 推测为：坏公司
['福利少', '加班少', '工资中', '压力小', '发展前景好', '氛围好', '位置近', '环境好'] 推测为：好公司

贝叶斯分类器(Bayes Classifier)

一、贝叶斯定理

相关文章

实验五贝叶斯分类器（模式识别与机器学习）

贝叶斯分类器详解

机器学习（六）——贝叶斯分类器

机器学习——贝叶斯分类器

贝叶斯分类器原理——学习笔记

机器学习-贝叶斯分类器（附Python代码）

chrome插件开发入门实战——CSDN免登陆拷贝、免关注查看

Github实用浏览器插件推荐

IDEA必备插件

Visual Studio 2017,C++MFC免注册调用大漠插件图文教程，详细版

PHPstorm必备插件推荐

【BurpSuite】插件之自用插件

插件的使用

TypechoCMS通用发布插件-【免登录版本】

【Unity插件】最多的插件合集

AS常用插件

油猴插件免费下载

超实用的浏览器插件：CSDN全站去广告

超实用的浏览器插件永久免费！！！

【Chrome必备插件，一键提升10倍效率】新用户永久免广告，好用！