目录
实验一 离散型数据的朴素贝叶斯分类
实验步骤:
NBtrain.m
NBtest.m
main.m
实验二 连续型数据的朴素贝叶斯分类
实验步骤:
naiveBayestrain.m
main.m
实验一 离散型数据的朴素贝叶斯分类
data数据集中含有625个样本,每个样本第1列为类别;2~5列为各样本的属性。

实验步骤:
① 准备阶段。
将数据集进行划分:训练集和测试集。
② 构建分类器,进行数据训练。
将数据集进行划分:训练集和测试集。
计算条件概率:根据每类中各属性取值的概率
③ 数据测试。
计算每个测试样本在其各属性下的条件概率;
计算测试样本对于各类别的判别概率;
NBtrain.m
function [y1,y_1,y2,y_2,y3,y_3] = NBtrain(train_data,train_label,m1)
% returen:
% y1 y2 y3 先验概率
% y_1,y_2,y_3 在第 ? 类的情况下,第i个属性取值为j的概率估计值%三类样本数量分别记为count1,count2,count3
count1=0;
count2=0;
count3=0;% 数据总共 3 个类别,4 个属性, 5 个取值。 %count_1(i,j)表示在第一类(y=1)的情况下,第i个属性是j的样本个数
count_1=zeros(4,5);
%count_2(i,j)表示在第二类(y=2)的情况下,第i个属性是j的样本个数
count_2=zeros(4,5);
%count_3(i,j)表示在第三类(y=3)的情况下,第i个属性是j的样本个数
count_3=zeros(4,5);%训练集样本数量 m1 = 562
for i=1:m1x=train_data(i,:);if train_label(i)==1count1=count1+1;for j=1:4 %指示第j个属性for k=1:5 %第j个属性为哪个值if x(j)==k%===========填空:对当前类别中第j个属性第k个值得个数进行统计=============count_1(j,k)=count_1(j,k)+1 ; %====================================================================break;endendendelseif train_label(i)==2count2=count2+1;for j=1:4 %指示第j个属性for k=1:5 %第j个属性为哪个值if x(j)==k%===========填空:对当前类别中第j个属性第k个值得个数进行统计=============count_2(j,k)=count_2(j,k)+1 ;%====================================================================break;endendendelse count3=count3+1;for j=1:4 %指示第j个属性for k=1:5 %第j个属性为哪个值if x(j)==k%===========填空:对当前类别中第j个属性第k个值得个数进行统计=============count_3(j,k)=count_3(j,k)+1 ;%====================================================================break;endendendendend%分别计算三类概率y1=p(y=1)、y2=p(y=2)、y3=p(y=3)的估计值%=========填空:计算每类的先验概率================
y1=count1/m1 ;
y2=count2/m1 ;
y3=count3/m1 ;
%===============================================%y_1(i,j)表示在第一类(y=1)的情况下,第i个属性取值为j的概率估计值
%y_2(i,j)表示在第二类(y=2)的情况下,第i个属性取值为j的概率估计值
%y_3(i,j)表示在第三类(y=3)的情况下,第i个属性取值为j的概率估计值
for i=1:4for j=1:5%=========填空:计算每类中每个属性的取值概率,即在第C类中第i个属性为k的条件概率=============y_1(i,j)= count_1(i,j)/count1 ;y_2(i,j)= count_2(i,j)/count2 ;y_3(i,j)= count_3(i,j)/count3;%====================================================================================end
endNBtest.m
function class_label = NBtest(test_data,y1,y_1,y2,y_2,y3,y_3,m2)
% y1 y2 y3 [1 1] 先验概率
% y_1,y_2,y_3 [4 5] 在第 ? 类的情况下,第i个属性取值为j的概率估计值class_label = [];
for i=1:m2xx=test_data(i,:);%==========填空:计算样本对于每类而言的后验概率=====================p1= y1 * y_1(1,xx(1)) * y_1(2,xx(2))*y_1(3,xx(3)) * y_1(4,xx(4));p2= y2 * y_2(1,xx(1)) * y_2(2,xx(2))*y_2(3,xx(3)) * y_2(4,xx(4));p3= y3 * y_3(1,xx(1)) * y_3(2,xx(2))*y_3(3,xx(3)) * y_3(4,xx(4));%============================================================ if p1>p2&&p1>p3class_label(i) = 1;endif p2>p1&&p2>p3class_label(i) = 2;endif p3>p1&&p3>p2class_label(i) = 3;endendmain.m
clear;
clc;
ex=importdata('data.txt'); %读入文件
X=ex.data;
Y = ex.rowheaders;
Y = grp2idx(Y); %将类别B,R,L化为1,2,3
m=size(X); %数据大小%训练集,测试集划分
ii=1;%用来标识测试集的序号
jj=1;%用来标识训练集的序号%我们把所有数字序号末尾为1的留作测试集,其他未训练集
for i = 1:mif mod(i,10)==1%%将数字序号末尾为1的留作测试集,其他未训练集test_data(ii,:)=X(i,:);test_label(ii)=Y(i);ii=ii+1;elsetrain_data(jj,:)=X(i,:);train_label(jj)=Y(i);jj=jj+1;endendm1=jj-1; %训练集样本数量562
m2=ii-1; %测试集样本数量63%y1、y2、y3表示每类的先验概率
%y_1(i,j)表示在第一类(y=1)的情况下,第i个属性取值为j的概率估计值
%y_2(i,j)表示在第二类(y=2)的情况下,第i个属性取值为j的概率估计值
%y_3(i,j)表示在第三类(y=3)的情况下,第i个属性取值为j的概率估计值[y1,y_1,y2,y_2,y3,y_3] = NBtrain(train_data,train_label,m1); %完善训练函数test_class = NBtest(test_data,y1,y_1,y2,y_2,y3,y_3,m2); %完善测试函数accuracy =length(find(test_label==test_class))/length(test_label)
cMat2 = confusionmat(test_label,test_class ) 实验二 连续型数据的朴素贝叶斯分类
fisheriris数据集中有150朵花的数据:
•meas给出了每朵花的4个属性:花萼长度,花萼宽度,花瓣长度,花瓣宽度。
•species说明了每朵花的种类:山鸢尾Setosa,杂色鸢尾Versicolour、弗吉尼亚鸢尾Virginica。

实验步骤:
•数据训练
1. 计算先验概率:每类样本占总样本数的比例;
2. 根据概率密度函数,计算各类样本中各属性取值的均值和方差。
•数据测试
1. 计算条件概率:根据训练集的均值与方差,计算训练样本的条件概率;
2. 计算测试样本对于类别的判别概率。
naiveBayestrain.m
function [label_priorP,mu,sigma] = navieBayestrain(meas,specise)
% means = 150 * 4
% specise = 150 * 1trainData = meas'; %训练数据集 4 *150
trainLabel = specise'; %训练类别集 1 * 150
classNum = length(unique(trainLabel)); %类别数 3label_priorP = zeros(1,classNum); %类别的先验概率 1*3%将trainSet按类别分组,然后分别对每类的数据求出每个属性的均值mu(Ak,Ci)和样本标准差sigma(Ak,Ci)
%mu(Ak,Ci),sigma(Ak,Ci)表示第Ci类数据集的属性Ak对应的均值和样本标准差groupedSet = cell(1,classNum); %空的分组数据集矩阵 1*3 3个块% eg
% C = {1,2,3;
% 'text',rand(5,10,2),{11; 22; 33}}
% C=2×3 cell array
% {[ 1]} {[ 2]} {[ 3]}
% {'text'} {5x10x2 double} {3x1 cell}%mu、sigma中每列为对应类的均值列向量和标准差向量,size(trainSet,1)-1表示样本的属性数att_number
%mu(attNum,classNum),sigma(attnum,classNum)分别是第classNum类的第attNum个属性的均值和标准差mu = zeros(size(trainData,1),classNum); % 4*3
sigma = zeros(size(trainData,1),classNum); % 4*3trainLabel = grp2idx(trainLabel);
% 分类过程,返回所有的分类索引trainLabel =trainLabel';
for sampleNum = 1:size(trainLabel,2) %size(trainLabel,2)为训练样本数label = trainLabel(1,sampleNum);%=====================================================================%%填空,计算每类样本的个数label_priorP(1,label) = label_priorP(1,label)+1;%=====================================================================%groupedSet{1,label} = [groupedSet{1,label} trainData(:,sampleNum)];
end
%=====================================================================%%填空,计算每类的先验概率label_priorP =label_priorP ./sampleNum;
%=====================================================================%%对于每一类 计算某类每个属性的均值和样本标准差for label = 1:classNum % 迭代每一类b = groupedSet{label}; % 4*50%=====================================================================%%填空,计算每类中每个属性的均值和标准差%第label个均值列向量;计算每类中每个属性的均值mu(:,label) = mean(b,2); %第label个标准差列向量;计算每类中每个属性的标准差;按行求标准差sigma(:,label) = std(b,0,2);
%=====================================================================%end
navieBayestest.m
function testClass = navieBayestest(meas,label_priorP,mu,sigma,classNum)% mu sigma 4*3 行属性 * 列类别testClass = [];
testData = meas' ; %测试数据集;testData每列代表一个样本 4 * 150test_number = size(testData,2);%测试集样本数
attr_number = size(testData,1);%测试集维数;每个样本的属性个数for testNum = 1:test_number % 循环测试样本X = testData(:,testNum); %当前测试样本 4 * 1
% prob = label_priorP;%先验概率
% for label = 1:classNum % 3类
% for k = 1:attr_number % 4属性
% %填空:计算每类的条件概率与后验概率
%
% %计算条件概率
% %此时prob已为后验概率
% Pxk = 1/ (sigma(k,label)*sqrt(2 * pi) )* exp(-((X(k,1)-mu(k,label))^2 )/(2*sigma(k,label)^2));
% prob(1,label) =prob(1,label) * Pxk;
% end
% %Pxk=1;
% end%% 考核:请在对数条件下实现方案一
%=====================================================================%prob = label_priorP;%先验概率%%计算测试样本对于每类的后验概率for label = 1:classNum % 3类for k = 1:attr_number % 4属性
%=====================================================================%%填空:计算每类的条件概率与后验概率%计算条件概率%此时prob已为后验概率Pxk = -log(sigma(k,label))-((X(k,1)-mu(k,label))^2 /(2 * sigma(k,label)^2));prob(1,label) =prob(1,label)+Pxk;
%=====================================================================%endend
%=====================================================================%[value index] = max(prob);testClass = [testClass index];
endmain.m
clc;
clear all;
tic
load fisheriris
% plotmatrix(meas)% meas 给出了每朵花的4个属性
% species 说明了每朵花的种类
[label_priorP,mu,sigma] = navieBayestrain(meas,species);%需完成函数 navieBayestrain()内的填空classNum = length(unique(species)); %类别数
testLabel = grp2idx(species);
testLabel =testLabel';testClass = navieBayestest(meas,label_priorP,mu,sigma,classNum);%需完成函数 navieBayestest()内的填空%识别率
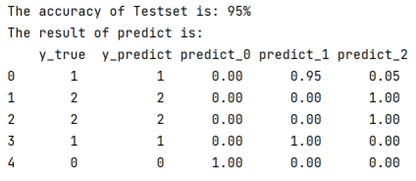
accuracy=length(find(testLabel==testClass))/length(testLabel)
cMat2 = confusionmat(testLabel,testClass )
toc