一天一个信号处理小知识 1.相位调制
引言
在通信系统中,当通信设备产生了需要发送的数据,这个数据为一长串比特流,如果使用示波器画出来,那么就是一连串的方波。要想进行通信,就必须得想办法通过空气将这串比特流发送到对方那里,但是受制于现实因素,如果直接将方波发送到空气中,那么性能将会惨不忍睹,为了改善这样的情况,就需要将比特流转化为一种便于发送的形式,即调制。
调制的方式有很多种,这里就只简单的讨论相位调制,比如QPSK, OQPSK, π / 4 \pi/4 π/4-QPSK
在探讨相位调制内容之前,我觉得很有必要先讨论一个问题:如何将数字比特信息映射到一个连续波形上?
波形映射
这个问题的回答可以有很多种,这里选用我比较喜欢的一种描述。
首先,在线性代数中有一个很重要的概念,就是基。比如在一个 R 2 R^2 R2空间中,向量 x = ( 1.0 ) x=(1.0) x=(1.0)和 y = ( 0 , 1 ) y=(0,1) y=(0,1)可以看成是这个空间的基,这个空间中的任何一个向量都可以用x和y的线性组合来表示,比如 A = ( a , b ) = a x + b y A=(a,b)=ax+by A=(a,b)=ax+by,进而任意一个向量都可以很简单地用这样一个数值对来表示。
那么现在思考,可不可能信号空间也可以使用这样的一对基来表示?这样就可以像上面一样将一个信号用一个数值对来表示。所以做如下假设:假设x(t)和y(t)是一对正交基,那么根据基的性质,它们的内积满足下列两个等式:
(注:以下的1234式的积分区间都是(0,T)即一个周期,因为懒得打所以没写在公式里)
∫ x ( t ) y ( t ) = 0 \int x(t)y(t)=0 ∫x(t)y(t)=0---------------------------------1
∫ x ( t ) x ( t ) = ∫ y ( t ) y ( t ) = c \int x(t)x(t) = \int y(t)y(t) =c ∫x(t)x(t)=∫y(t)y(t)=c--------------2
式1说明了正交基之间是正交的(这不是废话),式2说明了基的能量是一个常量。
假设存在这两个基之后,下一步需要做的就是如何用基来表示一个(能量有限的)信号,可以通过下式计算任意信号的坐标:
s I = ∫ s ( t ) x ( t ) s_I=\int s(t)x(t) sI=∫s(t)x(t)--------3
s Q = ∫ s ( t ) y ( t ) s_Q=\int s(t)y(t) sQ=∫s(t)y(t)--------4
3式和4式分别求出了类似 R 2 R^2 R2空间中的横纵坐标,可以用来唯一的指定一个信号。
进而这个信号就可以表示为: s ( t ) = s I x ( t ) + s Q y ( t ) s(t)=s_I x(t)+s_Qy(t) s(t)=sIx(t)+sQy(t),即表示为两个基的线性组合。
最终,有了上面的关系,现在我们只要确定一对合适的基即可。这里我们选择
x ( t ) = 2 ⋅ g ( t ) c o s ( 2 π f c t ) x(t) =\sqrt 2 ·g(t)cos(2\pi f_c t) x(t)=2⋅g(t)cos(2πfct)
y ( t ) = − 2 ⋅ g ( t ) s i n ( 2 π f c t ) y(t) =-\sqrt 2 ·g(t)sin(2\pi f_c t) y(t)=−2⋅g(t)sin(2πfct)
那么信号s(t)就可以表示为:
s ( t ) = s I x ( t ) + s Q y ( t ) = 2 s I ⋅ g ( t ) c o s ( 2 π f c t ) − 2 s Q ⋅ g ( t ) s i n ( 2 π f c t ) s(t)=s_Ix(t)+s_Qy(t)=\sqrt 2 s_I ·g(t)cos(2\pi f_c t)-\sqrt 2 s_Q ·g(t)sin(2\pi f_c t) s(t)=sIx(t)+sQy(t)=2sI⋅g(t)cos(2πfct)−2sQ⋅g(t)sin(2πfct)----------5
说明:其中 2 \sqrt 2 2是为了修正调制过程中的功率损失,g(t)是成型波形,用于将方波“盘”的更圆润,比如通过一个升余弦滚降滤波器。
到这一步,我们就可以很简单的使用 ( s I , s Q ) (s_I, s_Q) (sI,sQ)来在坐标系中表示一个信号。
得到了坐标,一下令人想起的,就是星座图。星座图反映了调制过程中符号的映射关系,由于在调制这步之前,我们需要将一个或者多个bit组合成符号,再对每一个符号赋予一个星座图中的坐标,那么根据之前的5式,我们就成功的将一个比特映射成了一个信号波形。
BPSK 和 QPSK
有了以上波形映射的知识,那么BPSK和QPSK就很好理解了。
由于BPSK一个bit为一个符号,所以星座图长这样:
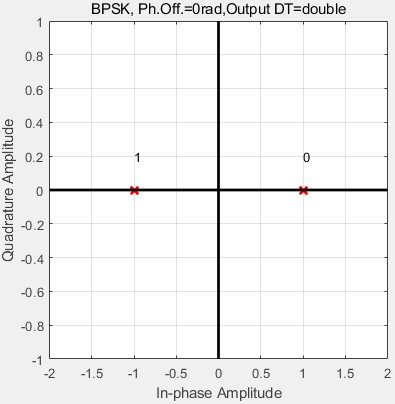
那么只需要根据5式,即可得到BPSK信号啦
同理,由于QPSK两个bit为一个符号,那么就有四个星座点,所以星座图长这样:
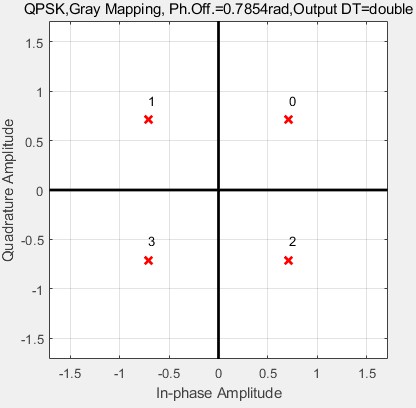
那么根据5式,即可得到QPSK信号。具体过程是,先对bit流进行串并转换,同时将0,1映射为1,-1,这样就得到了I Q两路数据流,将其看成方波,使用升余弦滚降滤波器进行波形成型,再分别和载波相乘进行变频,再相加就得到了最终发射波形。发射机架构见下图
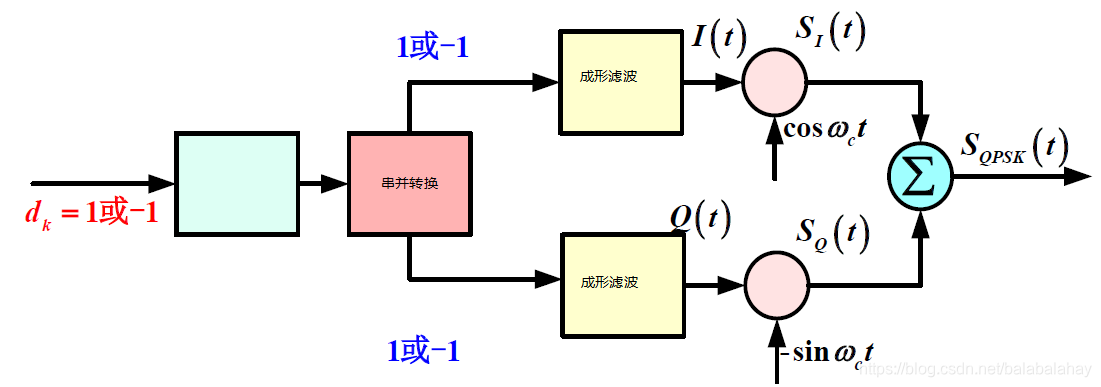
qpsk的星座图中有四个点,所以横纵坐标有四种组合方式,就是均匀分布在一个圆的四个点;对于8psk,横纵坐标就有八种组合方式,就是均匀分布在一个同心圆上的八个点
但是这样的一个过程和之前所说的波形映射之间又有什么联系呢?其实是这样的,在我们进行符号映射时,得到了两路数据,这两路分别是I路和Q路,而这两路数据其实就是星座图中点的横纵坐标。
OQPSK
qpsk有一个很大的问题,因为星座图之间的点之间可以随意的互相跳变,那么其最大相位变化即为180度,这就使得信号的带宽增加,解决办法就是尽可能减少180度的跳变,就出现了oqpsk的做法。
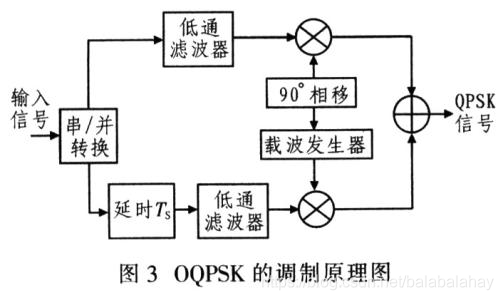
由于在进行串并转换的过程中,信号速率降低为原来的一半,如果原来的码元周期为T,那么现在即为2T,所以将并行码元的其中一路进行1T的延时,就可以使得两个符号之间的跳变不会出现180度,只会是90度跳变,系统结构见上图。
π / 4 \pi/4 π/4- QPSK
π / 4 \pi/4 π/4- QPSK的大体思路和前两种相似,不同的是,调制出的相位信息不是绝对相位,而是相位差,即每一个调制信号的相位,都是当前相位差加上之前的累积相位,这有个好处就是,可以使得解调可以使用非相干解调,不需要载频的参与,降低了接收端同步的需求。
这样调制的结果是,星座图变成了8psk的形式,但是相位跳变只有45度和135度两种情况。