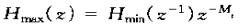数字滤波器(二)--最小相位延时系统和全通系统

article/2025/8/23 19:52:35

最小相位延时系统和全通系统

- - 引
  - 1. 系统相位
  - 2. 最小相位延时系统
  - - - 2.1 最小相位延时系统
      - 2.2 最小相位延时系统的性质
  - 3. 全通系统
  - - - 3.1 定义与系统函数
      - 3.2 全通系统的零极点关系
      - 3.3 全通系统的应用

引

数字滤波器(一)–IIR与FIR的基本结构与MATLAB实现

1. 系统相位

当输入信号经过一个滤波器系统的时候，其相位可能会发生一定的移动，那么一个系统的相位到底跟什么有关系呢？对于给定的系统：
在这里插入图片描述
其系统相位的延迟可以这么表达：

2. 最小相位延时系统

2.1 最小相位延时系统

什么是最小相位延时系统呢？顾名思义，就是对输入信号的相位移动延时最小的系统。
对于第一节中的系统 $H (z)$ ，我们假设系统有M个零点，N个极点，我们可以定义一下参数：
$m_i$ ：单位圆内的零点数
$m_o$ ：单位圆外的零点数
$p_i$ ：单位圆内的极点数
$p_o$ ：单位圆外的极点数
所以我们可以得到 $m_i+m_o=M$ , $p_i+p_o=N$

对于因果稳定系统，其系统函数的全部极点都在单位圆内(划重点，要考的！)，所以 $p_i=N, p_o=0$

我们来观察一下系统零极点对相位的影响：
当数字频率ω从0变化到2π时，相位的变化可以表示为：
在这里插入图片描述
此时幅角变化为负，因此相位产生了延时，此时系统称为相位延时系统。相位角的变化大小与单位圆外的零点数目有关：

当零点全部位于单位圆之内时， $m_i=M,m_o=0$ ,此时相位变化最小：

称此系统为最小相位延迟系统。
当零点全部位于单位圆之外时， $m_i=0,m_o=M$ ，此时相位变化最大：

称此系统为最大相位延迟系统。

对于延时系统的定义，我们可以参照此表：(我们可以通过判断系统的零点和极点相对于单位圆的位置来对延迟系统进行分类)
在这里插入图片描述

2.2 最小相位延时系统的性质

最小相位延迟系统有怎么样的性质呢？

在幅频响应相同的所有系统中，最小相位延迟系统的单位序列响应的能量集中在n=0附近。
在幅频响应相同的所有系统中，最小相位延迟系统具有最小的群延时。
任何因果稳定的非最小相位延时系统 $H (z)$ 都可以表示为全通系统与最小相位延时系统的级联。(这个性质在后面讲解滤波器设计的时候很重要)

3. 全通系统

3.1 定义与系统函数

系统频率响应的幅度在所有频率下均为1或常数，这样的系统称为全通系统，也就是说全通系统是指不改变信号幅度谱，只改变相位谱的信号处理系统。

全通系统的系统函数可以表示为：
在这里插入图片描述
其中 $D(z)=1+a_1z^{-1}+a_2z^{-2}+...+a_Nz^{-N}$ ,是关于 $z^{-1}的N次多项式$ ，N是系统的阶数。

一阶全通系统的系统函数可以表示为：
在这里插入图片描述
二阶全通系统的系统函数可以表示为：

3.2 全通系统的零极点关系

对于全通系统：
在这里插入图片描述
我们可以知道，如果系统函数存在极点 $z=z_1=re^{jθ}$ ，则系统函数一定存在零点 $z=\frac{1}{z_1}=\frac{1}{r}e^{-jθ}$
因为系统函数分子分母的系数均为实数，因此零极点均以共轭对的形式出现，所以也会存在对应的共轭极点 $z=z_1^*=re^{-jθ}$ 和共轭零点 $z=\frac{1}{z_1^*}=\frac{1}{r}e^{jθ}$ .

总结一下，全通系统的零极点可以表示为：
在这里插入图片描述
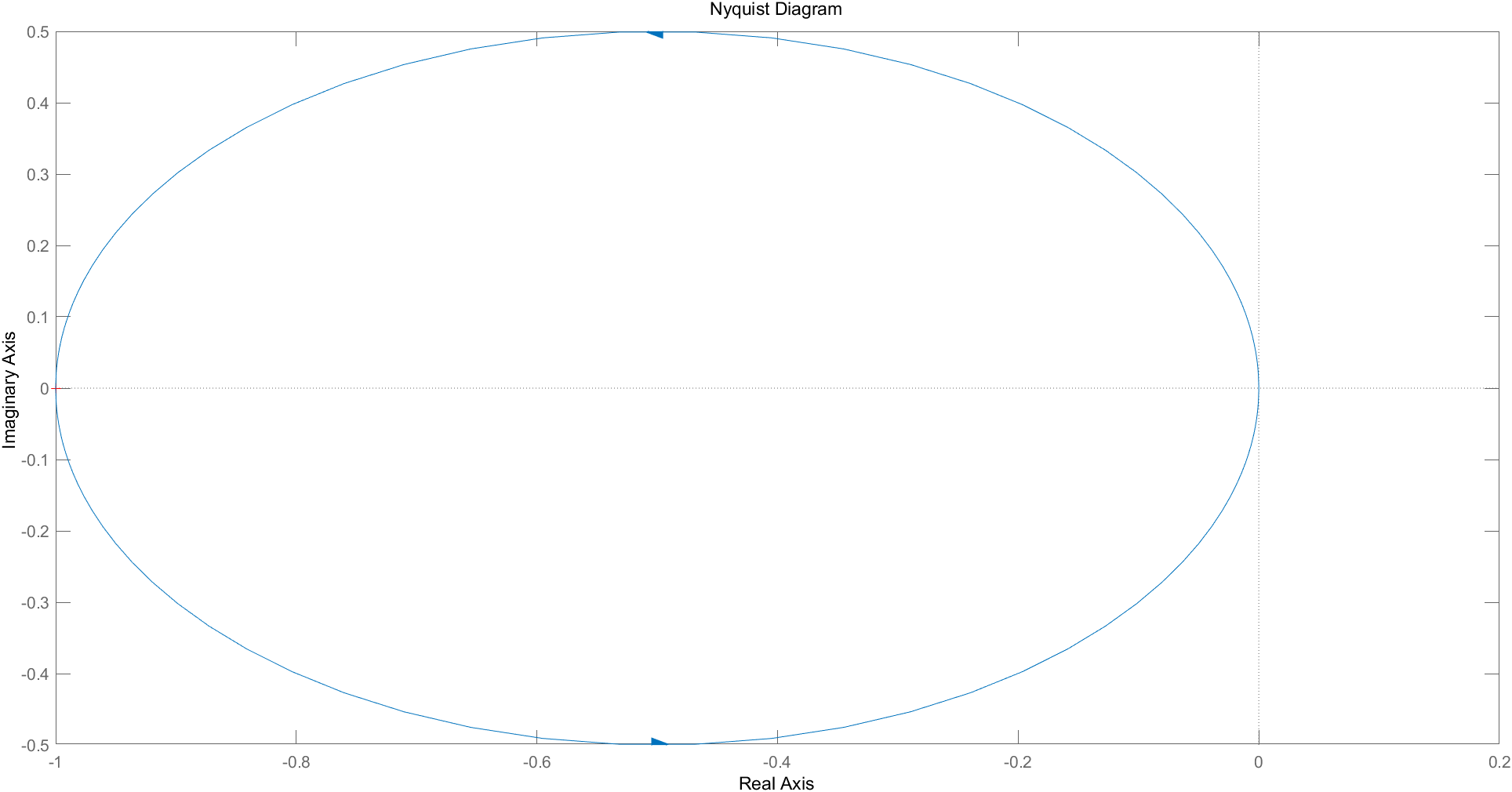
将这两对零极点作为零极点分布图，可以表示为：

可以发现，全通系统的零极点出现在共轭反演的位置上。

我们可以通过一个例子来熟悉一下全通系统零极点之间的关系：

在这里插入图片描述
首先，我们将系统的差分方程转化为系统传递函数为：

从系统函数可以得到该系统的零点为 $z_0=-b$ , 极点 $z_p=a$ ，根据全通系统零极点互为共轭反演的关系，即 $z_0=\frac{1}{z_p}$ ,可以得到b需要满足以下条件：
在这里插入图片描述

3.3 全通系统的应用

我们可以通过零极点对消的方式，实现系统之间的转化。
① 任何因果稳定的最小相位延时系统，都可以表示为全通系统与最小相位延时系统的级联，即：
在这里插入图片描述
所得系统函数与最小相位系统的差别，只是频率响应的相位不同。我们可以通过下面这个零极点图来表示该转化关系：

从上图我们可以看出，全通系统中的两个极点(红色叉标注)与最小相位延时系统中的两个对应的零点(红色圈标注)互相抵消了。

② 可以使用级联全通系统的方法，是的一个非稳定的滤波器转化为稳定的系统。
我们通过零极点图来反应这一关系：
在这里插入图片描述
因为稳定系统的极点必须都在单位圆内，上图中非稳定系统的蓝色标记的极点显然在圆外面，我们可以通过级联一个全通系统来抵消这个极点。因为全通系统的零极点是共轭反演的，所以两个红色圈标记的零点对应两个单位圆内的零点。通过级联之后，全通系统的单位圆外的零点与非稳定系统的单位圆外的极点相互抵消，从而使系统稳定。

我们可以通过一个例子来更加理解全通系统的应用：

在这里插入图片描述
根据系统传递函数，我们可以得到该系统的零点为：

该系统的极点为：

表示在单位圆上为：

它可以表示为一个最小相位延时系统和一个全通系统的级联：

最小相位延时系统中的两个红色标记的零点和全通系统中两个红色标记的极点通过级联相互抵消。用公式表示上述关系：
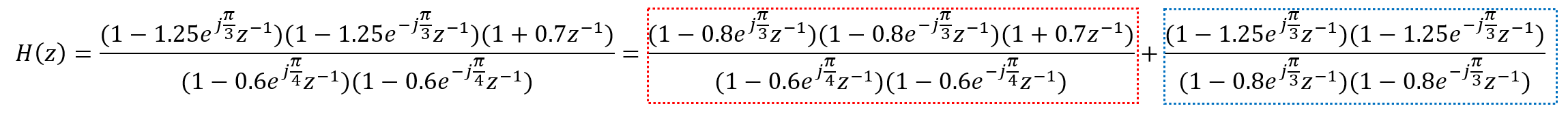
在这里插入图片描述
其中红色框表示最小相位延时系统的传递函数，蓝色框表示全通系统的传递函数。