注：本博客是基于奥本海姆《离散时间信号处理》第三版编写，主要是为了自己学习的复习与加深。

 

一、最小相位系统

一）、最小相位和全通系统

1、任何有理系统函数都能表示成

式5.1

式中是最小相位系统，是全通系统。

1）、包含H(z)中位于单位圆内的零、极点，再加上H(z)中单位圆外的零点成共轭倒数的那些零点。

2）由全部H(z)中位于单位圆外的零点和与中反射过来的共轭倒数零点相抵消的极点组成。

 

2、利用式5.1可以从一个最小相位系统把其一个或多个位于单位圆内的零点反射到单位圆外与它们成共轭倒数的位置上面形成一个非最小相位系统；或者相反，从一个非最小相位系统把全部位于单位圆外的零点反射到单位圆内与其成共轭倒数的位置上而形成一个最小相位系统。在任意情况下，这个最小相位与非最小相位系统都具有相同的频率响应幅度。

 

二）、非最小相位系统的频率响应补偿

1、在很多信号处理范畴内，一个信号已经被某个不合要求的频率响应德LTI系统所失真，然后可能关心德是要用到一个补偿系统来处理这个失真德信号，如图1所示。

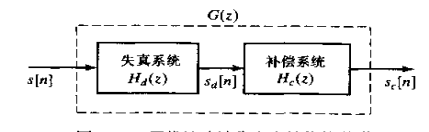图1

1）、如果实现完全的补偿，那么sc[n]=s[n]，也就是说，Hc[z]就是Hd[z]的逆系统。

2）、如果假定失真系统是稳定和因果德，并且要求补偿系统也是稳定和因果德，那么只有当Hd[z]是最小相位系统而有一个稳定和因果的逆系统时，这种完全的补偿才有可能。

 

2、Hd(z)和Hdmin(z)有相同的频率响应幅度，并且通过一个全通系统Hap（z）联系在一起，即

式5.2

选取补偿滤波器为

式5.3

联系sc[n]和s[n]的总系统函数是

式5.4

即G(z)相当于一个全通系统。结果，就完全不唱了频率响应幅度，而相位响应则被调整为。

 

 

三）、最小相位系统的性质

1、最小相位滞后性质：一个全通系统的连续相位曲线在0≤w≤Π总是负的。因此，将Hmin(z)的零点从单位圆内反射到单位圆外其共轭倒数的位置上总是使(连续)相位减少，或者说使相位的负值增加，这就称之为相位滞后函数。这样具有幅度响应为|Hmin(ejw)|，全部零点（当然还是极点）都位于单位圆内的因果稳定的系统对于具有相同幅度响应的所有其他系统而言就具有最小滞后函数（0≤w≤Π）。

 

2、最小群延迟性质：全通系统具有这样一个一般性质：它们对全部w总是有正德群延迟。因此，如果还是考虑全部都有给定幅度响应|Hmin(ejw)|德系统，那么全部零、极点都在单位圆内德系统就有最小德群延迟。

 

3、最小能量延迟性质：

式5.5

根据式（5.5），最小相位系统德部分能量集中在n=0周围，也就是说，最小相位（滞后）系统也称为最小能量延迟系统，简称最小延迟系统。

 

 

二、广义线性相位德线性系统

一）、线性相位系统

1、考虑一个LTI系统，其响应在一个周期内是

式5.6

式中α是实数，但不一定是整数。这样的系统是一个“理想延迟”系统，这里的α是由该系统引入德延迟。

1）、可看出该系统有恒定的幅度相应、线性相位和恒定群延迟，即

式5.7

式5.8

式5.9

2）、的傅里叶逆变换就是单位脉冲响应，为

式5.10

3）、对输入x[n]，该系统的输出是

式5.11

若α=nd，那么就有

式5.12

和

式5.13

也就是说，如果α=nd是一个整数，那么具有线性相位和单位增益的式（5.6）系统知识输入序列移动nd个样本。

 

2、对于α不是整数的讨论：具体来说式(5.6)系统的一种如图2所示，

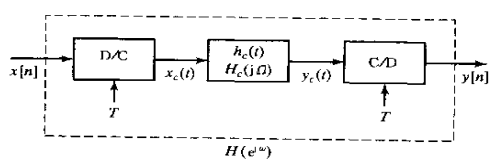图2

其中和，使得

式5.14

对x[n]原来是否是经由采样一个连续时间信号得到的，这种表示都是正确的。按照图2的表示y[n]就是输入序列带线内插时移后的样本序列，即式(5.6)的系统就是具有α样本的延迟，即使α不是整数。

 

3、理想延迟系统的讨论，也给出了对具有非恒定幅度频率响应的线性相位一种有用的解释。

 

4、一般而言，一个线性相位系统具有频率响应为

式5.15

1）、如果2α是整数（即α为整数或为一个整数再加1/2），那么相应的单位脉冲响应关于α就是偶对称的，即

式5.16

2）、如果α不是一个整数，那么单位脉冲响应就不具有对称性。

 

二）、广义线性相位

1、如果系统的频率响应能表示成

式5.17

就说明该系统是一个广义线性相位系统。

1）、这里的α和β都是常熟，而A(ejw)是w的实（可能由正负）函数。

2）、如果不顾及在整个|w|<Π的频带或者部分频带内由于附加固定相位项而带来的不连续性的话，那么这类系统也能用恒定群延迟来表征这就是具有

式5.18

的这类系统具有更一般的线性相位形式为

式5.19

式中α和β都是实数。

 

2、线性相位系统的单位脉冲响应在2α为整数时，对α可以具有对称性。由此导出如下一个对恒定群延迟系统h[n],α和β都必须满足的方程。

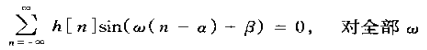式5.20

这个方程对于具有恒定群延迟的系统时关于h[n]，α和β的一个必要条件。

 

3、广义线性相位系统的例子

1）、满足以下条件的系统

式5.21a

式5.21b

式5.21c

有了β不是=0或Π，式(5.20)就变成

式5.22

由此可以证明，如果2α时整数，式(5.24)中的各项就能配对，一使得组成的每一对对全部w都恒为零。

2）、满足以下条件

式5.23a

式5.23b

式5.23c

式(5.23)就意味着频率响应具有式（5.17）的形式，这时，式（5.22）就变为

式5.24

且该式对所有w都成立。

 

三）、因果广义线性相位系统

1、如果系统时因果的，那么式（5.22）就变成

式5.25

因果性和式（21）、式（5.23）的条件就意味着

式5.26

也就是说，如果系统单位脉冲响应的长度为(M+1)，并满足式（5.21c）或式（5.23c），那么因果FIR系统就具有广义线性相位。具体来说；

1）若

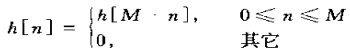式5.27a

就能证明

式5.27b

式中是w的实、偶和周期函数。

2）、若

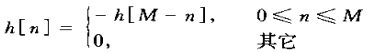式5.28a

就能证明

式5.28b

式中是w的实、偶和周期函数。应该注意在两种情况下，单位脉冲响应的长度都是（M+1）个样本。

3）、式（5.27）和式（5.28）对保证具有广义线性相位的因果系统都是充分条件。然而他们都不是必要条件。

 

2、FIR线性相位系统频率响应表达式在滤波器设计和理解这类系统的某些性质上是有用的。在导出这些表达式时，会发现能得出一些明显不同的表达式。这取决于对称的形式和M时偶数还是奇数。为此，定义4种类型的FIR广义线性相位系统一般是有用的。

I类FIR线性相位系统

I类系统时定义为具有如下面对称单位脉冲响应特性的系统

式5.29

其中M为偶整数。延迟M/2也是整数，频率响应是

式5.30a

这里

式5.30b

式5.30c

于是，由式（5.30a）可见具有式（5.27b）的形式，特别是相应于式（5.17）中的β不是0就π。

II类FIR线性相位系统

II类系统有式（5.29）的对称单位脉冲相应特性，这里M为奇整数。这里的H(ejw)可表示为

式5.31a

式中

式5.31b

具有式（5.27b）的形式，其延迟为M/2。这是就是一个整数加上半个样本间隔的延迟，而相应于式（5.17）中的β是0或π。

III类FIR线性相位系统

如果系统具有如下反对称单位脉冲响应特性：

式5.32

其中M为偶数，那么就具有

式5.33a

这里

式5.33b

这里具有式（5.28b）的形式，其延迟为M/2，是一个整数，而对应于式（5.17）中的β是π/2或3π/2。

IV类FIR线性相位系统

如果单位脉冲响应特性是式（5.32）的反对称，而M为奇函数，那么

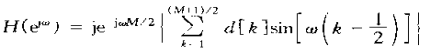式5.34a

这里

式5.34b

与III类系统的情况相同，具有式（5.28b）的形式，其延迟为M/2，是一个整数再加上半个样本间隔的延迟，而相应于式（5.17）中β就是π/2或3π/2。

FIR线性相位系统的零点位置

考虑一下FIR线性相位系统的系统函数零点的位置。它们的系统函数是

式5.35

1）、在对称的情况下（I和II类），能用式（5.29）来表示H(z)为

式5.36

由式（5.153）得出，如果z0是H(z)的零点，那么

式5.37

者意味着：若是H(z)的零点，那么也是H(z)的零点。当h[n]为实数且z0是H(z)的零点时，那么也一定时H(z)的零点，并且按照前述能够推得也是H(z)的零点。因此，当h[n]是实数时，不在单位圆上的每个复数零点一定时一组4个如下形式的共轭倒数零点中的一个：

如果H(z)的零点在单位圆上，即，那么，所以单位圆上的零点以如下形式成对出现：

如果H(z)的零点是实数但不在单位圆上，其倒数也一定是H(z)的零点，H(z)将有如下因子：

最后，H(z)在z=±1的零点，因为±1的倒数和共轭还是±1，所以只能以z=±1出现。因此，H(z)也可有如下因子

零点在z=-1的情况很重要。根据式（5.36）

如果M为偶数，这就是一个简单的恒等式：但若M为奇数，H(-1)=-H(-1)，则H(-1)必须是零。据此，对于M为奇数的对称脉冲响应，其系统函数必须有一个零点在z=-1。图3（a）和（b）分别表示I类（M为偶数）和II类（M为奇数）系统的典型的零点位置。

图3

2）、如果单位脉冲响应式反对称的（III类和IV类），那么遵循上面得出式（5.29）的办法，可以证明有

式5.38

这个式子用来说明对于反对称情况，H(z)的零点也和对称情况下的零点一样收到约束。然而，在反对称情况下，z=1和z=-1都具有特殊的意义。若z=1，式（5.38）就变成了

H(1)=-H(1)式（5.39）

于是H(z）必须有z=1的零点，不论M为偶数还是奇数。若z=-1，式（5.38）给出

式（5.40）

这时，若（M-1）为奇数（M为偶数），H(-1)=-H(-1)，所以z=-1在M为偶数时必须时H(z)的零点。图3(c)和(d)分别示出了III类和IV类系统典型的零点位置。

 

四）、FIR线性相位系统与最小相位系统的关系

1、以上的讨论表明，所有单位脉冲响应为实的FIR线性相位系统，其零点不是在单位圆上就是在共轭倒数的位置上。因此，很容易证明，任何FIR线性相位系统的系统函数都能因式分解为最小相位项Hmin(z)、最大相位项Hmax（z）以及仅包含单位圆上的零点的项Huc（z），即

式（5.41a）

这里

式（5.41b）

Mi是Hmin（z）零点的个数。在式（5.41a）中，Hmin（z）的全部Mi个零点都在单位圆内，而Huc（z）的全部Mo个零点都在单位圆上。Hmax（z）的全部Mi个零点都在单位圆外。并且从式（5.41b）可知，它的零点就是Hmin（z）的Mi个零点的倒数。因此，系统函数H(z)的阶就是M=2Mi+Mo。