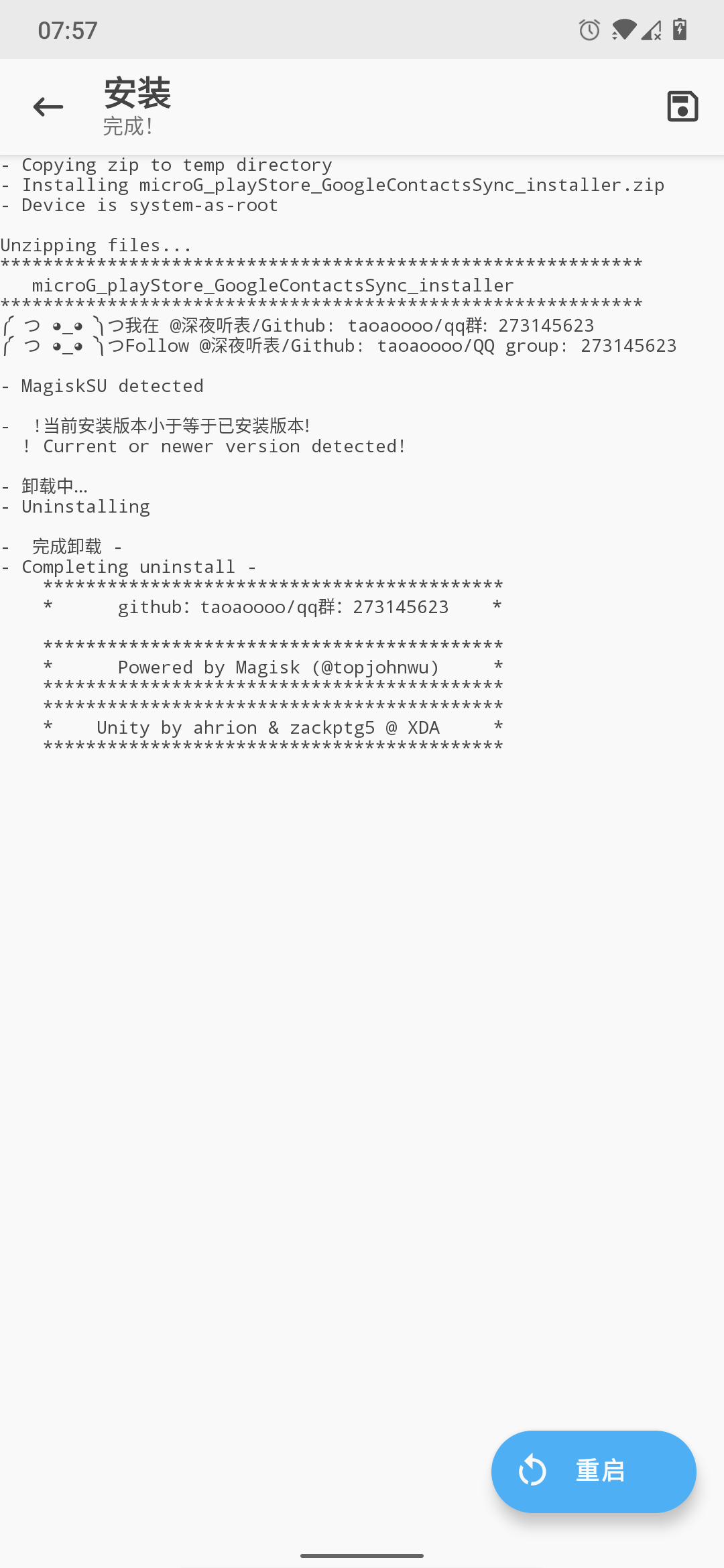
扫描区别
在电视的标准显示模式中,i表示隔行扫描,p表示逐行扫描。






隔行扫描视频编码(interlaced-scan video coding)
隔行扫描图像的每帧包括两个场,所以对于隔行扫描图像有三种编码方式:
1、将两场合并为一帧进行编码;
2、将两场分别编码;
3、将两场合 并为一帧,但是在宏块级别上,将一个帧宏块划分为两个场宏块进行编码。
前两种编码方式称为图像自适应帧/场编码(Picture-adaptive frame-field, PicAFF or PAFF)
第三种称为宏块自适应帧/场编码(Macroblock-adaptive frame-field, MBAFF)。
- PAFF:对于一个运动图像,由于场之间存在着较大的扫描间隔,所以帧中相邻两行之间的空间相关性相对于逐行扫描图像较小,因此对两个场分别编码 会更节省码流。对于一个非运动图像,相邻两行之间存在较大的空间相关性,将两场合并为一帧编码更有效。所以PAFF编码方式可以针对整个图像的编码方式做 自适应调整,选择帧编码或场编码。
- MBAFF:当图像同时存在运动区域和非运动区域时,PAFF的劣势便显现出来,PAFF的自适应粒度太粗,无法实现满足更加精细的编码要求,于 是MBAFF应运而生。MBAFF对帧编码或场编码的选择是基于宏块的,MBAFF将两场合并为一帧进行编码,但将每一个帧宏块(16x16)划分为场宏 块对(8x16),针对每一个帧宏块,比较帧编码和场编码产生的码流大小,使用最节省码流的方式。
运动补偿
一种描述相邻帧(相邻在这里表示在编码关系上相邻,在播放顺序上两帧未必相邻)差别的方法,具体来说是描述前面一帧(相邻在这里表示在编码关系上的前面,在播放顺序上未必在当前帧前面)的每个小块怎样移动到当前帧中的某个位置去。这种方法经常被视频压缩/视频编解码器用来减少视频序列中的时域冗余。它也可以用来进行去交织(deinterlacing)以及运动插值(motion interpolation)的操作。
一个视频序列包含一定数量的图片--通常称为帧(frame)。相邻的图片通常很相似,也就是说,包含了很多冗余。使用运动补偿的目的是通过消除这种冗余,来提高压缩比。
最早的运动补偿的设计只是简单的从当前帧中减去参考帧,从而得到通常含有较少能量(或者称为信息)的"残差",从而可以用较低的码率进行编码。解码器可以通过简单的加法完全恢复编码帧。
一个稍微复杂一点的设计是估计一下整帧场景的移动和场景中物体的移动,并将这些运动通过一定的参数编码到码流中去。这样预测帧上的像素值就是由参考 帧上具有一定位移的相应像素值而生成的。这样的方法比简单的相减可以获得能量更小的残差,从而获得更好的压缩比--当然,用来描述运动的参数不能在码流中 占据太大的部分,否则就会抵消复杂的运动估计带来的好处。
通常,图像帧是一组一组进行处理的。每组的第一帧(通常是第一帧)在编码的时候不使用运动估计的办法,这种帧称为帧内编码帧(Intra frame)或者I帧。该组中的其它帧使用帧间编码帧(Inter frame),通常是P帧。这种编码方式通常被称为IPPPP,表示编码的时候第一帧是I帧,其它帧是P帧。
在进行预测的时候,不仅仅可以从过去的帧来预测当前帧,还可以使用未来的帧来预测当前帧。当然在编码的时候,未来的帧必须比当前帧更早的编码,也就是说,编码的顺序和播放的顺序是不同的。通常这样的当前帧是使用过去和未来的I帧或者P帧同时进行预测,被称为双向预测帧,即B帧。这种编码方式的编码顺序的一个例子为IBBPBBPBBPBB。