马氏距离详解
- 一、理性认知
- 二、感性认知
- 第一个例子
- 第二个例子
- 三、实例认知
- 四、公式推导
- 推导过程
- 致谢
一、理性认知
马氏距离(Mahalanobis distance)是由印度统计学家马哈拉诺比斯(P. C. Mahalanobis)提出的,表示点与一个分布之间的距离。它是一种有效的计算两个未知样本集的相似度的方法。与欧氏距离不同的是,它考虑到各种特性之间的联系(例如:一条关于身高的信息会带来一条关于体重的信息,因为两者是有关联的),并且是尺度无关的(scale-invariant),即独立于测量尺度。对于一个均值为μ,协方差矩阵为Σ的多变量向量,其马氏距离为sqrt( (x-μ)'Σ^(-1)(x-μ) )。(百度百科)
二、感性认知
第一个例子
从下往上的一段50米长的坡道路,下面定一个A点,上面定B一个点。假设有两种情况从A到B:
a)坐手扶电梯上去。
b)从手扶电梯旁边的楼梯爬上去。
两种情况下我们分别会产生两种不同的主观感受,坐电梯轻松愉快,感觉很快就从A到了B——“A与B真近~”;走楼梯爬的气喘吁吁很累,感觉走了好久才走到B——“A与B真远!”。
第二个例子
观看落日之时,由于大气的折射效应,太阳形状产生形变并且视觉位置也比真实位置高。
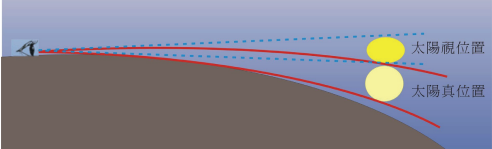
三、实例认知
马氏距离有些统计上的意味,下式中的S指协方差(同Σx )

与欧式距离的差距来自下图,欧式是强行求距离,而马氏是经过一个寻找最适坐标位置(更看重当前点在各维度的地位)。嘛…有点PCA的韵味在里面。


四、公式推导
首先我们先看个二维的例子。
此例的数据重心为原点,P1,P2到原点的欧氏距离相同,但点P2在y轴上相对原点有较大的变异,而点P1在x轴上相对原点有较小的变异。所以P1点距原点的直观距离是比P2点的小的。
马氏距离就是解决这个问题,它将直观距离和欧式距离统一。为了做到这一点, 它先将数据不同维度上的方差统一(即各维度上的方差相同),此时的欧式距离就是直观距离。
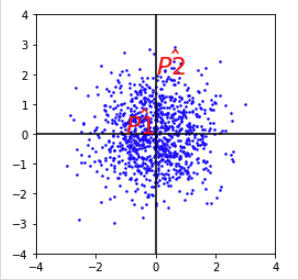
如图:统一方差后的图,P1’到原点的距离小于P2’。P1’到原点的欧式距离和P2’的相同。以上所说的直观距离就是马氏距离 。但是,如果不同维度之间具有相关性,则压缩的效果就不好了。如下图只在横向和纵向上压缩,则达不到上图的压缩效果。

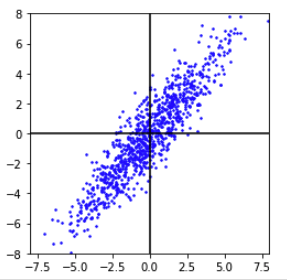
所以在F1方向和F2方向上压缩数据才能达到较好的效果。所以需要将原始数据在XY坐标系中的坐标 表示在F坐标系中。然后再分别沿着坐标轴压缩数据。
所以,计算样本数据的马氏距离分为两个步骤:
1、坐标旋转
2、数据压缩
坐标旋转的目标:使旋转后的各个维度之间线性无关,所以该旋转过程就是主成分分析的过程。
数据压缩的目标:将不同的维度上的数据压缩成为方差都是1的的数据集。
推导过程
有一个原始的多维样本数据Xn×m(m列,n行):
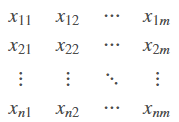
其中每一行表示一个测试样本(共n个);Xi表示样本的第i个维度(共m个) Xi=(x1i,x2i,…,xni)T ,以上多维样本数据记为X=(X1,X2⋯Xm)。样本的总体均值为μx=(μx1,μx2⋯μxm)。其协方差为:
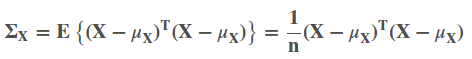
协方差矩阵表示样本数据各维度之间的关系的。其中n是样本的数量
假设将原始数据集X通过坐标旋转矩阵U旋转到新的坐标系统中得到一个新的数据集F。(其实X和F表示的是同一组样本数据集,只是由于其坐标值不同,为了易于区分用了两个字母表示)
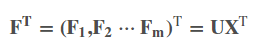
新数据集F的均值记为μF = μF1, μF2⋯ μFm , μF = Uμx
由于将数据集旋转后数据的各维度之间是不相关的,所以新数据集F的协方差矩阵ΣF应该为对角阵。
由于:
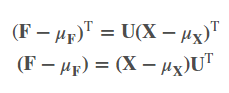
所以:
其中sqrt(λi)就是第i个维度的方差。
由于Σx是实对角阵,所以U是一个正交矩阵 UT=U-1。
以上是准备知识,下面推导一个样本点x=(x1,x2⋯xm)到重心μX=(μX1,μX2⋯μXm)的马氏距离。等价于求点 f=(f1,f2⋯fm) 压缩后的坐标值到数据重心压缩后的坐标值 μF=(μF1,μF2⋯μFm)的欧式距离。
这就是马氏距离的的计算公式了。
如果x是列向量
d2 = ( x − μx )T Σ-1X ( x − μx )
如果并把上文的重心 μx = ( μx1, μx2⋯ μxm) 改为任意一个样本点y,则可以得到x和y两个样本点之间的马氏距离公式为:
d2 = ( x − y )TΣ-1x ( x − y )
致谢
工作中遇到了马氏距离,多方查找资料,才对马氏距离有一个全面的认识。在此,将自己在学习过程中认为比较重要的点整理如上,感谢前辈大佬们的分享!