【状态机设计】Moore、Mealy状态机、三段式、二段式、一段式状态机书写规范

article/2025/9/19 23:09:45

目录

状态机介绍

状态机类型

Moore 型状态机

Mealy 型状态机

状态机设计流程

自动售卖机

状态机设计：3 段式（推荐）

实例

实例

状态机修改：2 段式

实例

状态机修改：1 段式（慎用）

实例

状态机修改：Moore 型

实例

实例

 

状态机介绍

有限状态机（Finite-State Machine，FSM），简称状态机，是表示有限个状态以及在这些状态之间的转移和动作等行为的数学模型。状态机不仅是一种电路的描述工具，而且也是一种思想方法，在电路设计的系统级和 RTL 级有着广泛的应用。

都说状态机是 FPGA 设计的灵魂，可见其重要之处，在 Verilog 的设计中，状态机其实可以等同于 if 语句和 case 语句，但是由于在某些情况下，状态的种类多且复杂，各种状态跳转起来非常麻烦，所以 一般利用状态机设计是一种可靠便捷的方法。

规范的状态机代码可以极大地提高设计效率， 在减少状态出错可能的同时缩短调试时间， 从而设计出稳健的系统。

在设计状态机时，最好能够满足以下要求：

  • 通用的设计方法， 针对简单或复杂的状态机设计都能满足；
  • 步骤清晰易懂， 每步只考虑一个问题；
  • 状态机代码严谨规范， 不容易出错；
  • 设计的状态机结构简单且稳定。

状态机类型

Verilog 中状态机主要用于同步时序逻辑的设计，能够在有限个状态之间按要求和规律切换时序电路的状态。状态的切换方向不但取决于各个输入值，还取决于当前所在状态。 状态机可分为两类：

  • Moore 状态机
  • Mealy 状态机

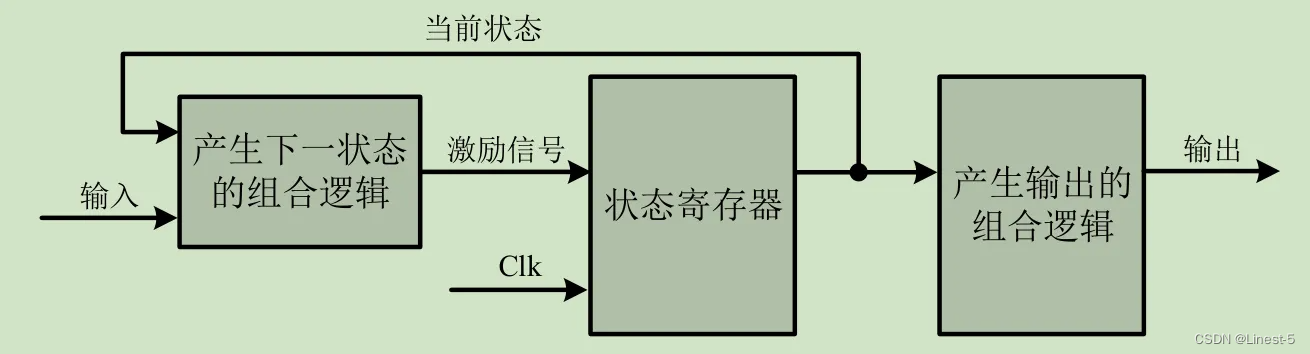
Moore 型状态机

Moore 型状态机的输出只与当前状态有关，与当前输入无关。

输出会在一个完整的时钟周期内保持稳定，即使此时输入信号有变化，输出也不会变化。输入对输出的影响要到下一个时钟周期才能反映出来。这也是 Moore 型状态机的一个重要特点：输入与输出是隔离开来的。

4d4c3c3c99964c879e4ea6c46e5e9e6a.png

 

 

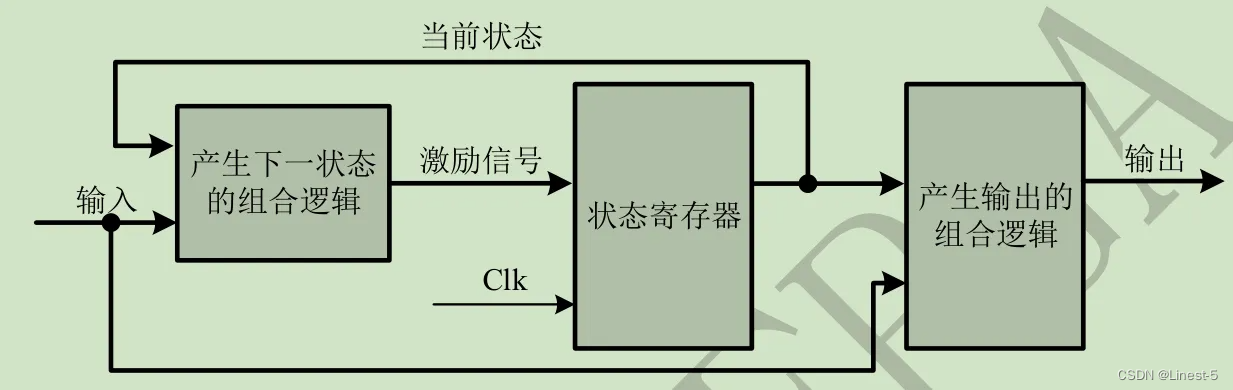
Mealy 型状态机

Mealy 型状态机的输出，不仅与当前状态有关，还取决于当前的输入信号。

Mealy 型状态机的输出是在输入信号变化以后立刻发生变化，且输入变化可能出现在任何状态的时钟周期内。因此，同种逻辑下，Mealy 型状态机输出对输入的响应会比 Moore 型状态机早一个时钟周期。

1b209e2630964d6f95af242981dc3290.png

 

 

状态机设计流程

根据设计需求画出状态转移图，确定使用状态机类型，并标注出各种输入输出信号，更有助于编程。一般使用最多的是 Mealy 型 3 段式状态机，下面用通过设计一个自动售卖机的具体实例来说明状态机的设计过程。

自动售卖机

自动售卖机的功能描述如下：

饮料单价 2 元，该售卖机只能接受 0.5 元、1 元的硬币。考虑找零和出货。投币和出货过程都是一次一次的进行，不会出现一次性投入多币或一次性出货多瓶饮料的现象。每一轮售卖机接受投币、出货、找零完成后，才能进入到新的自动售卖状态。

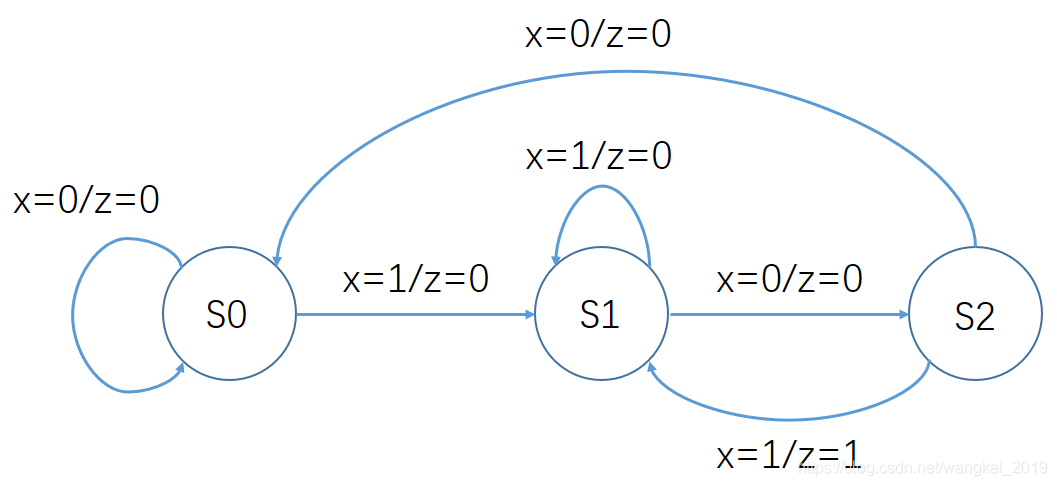
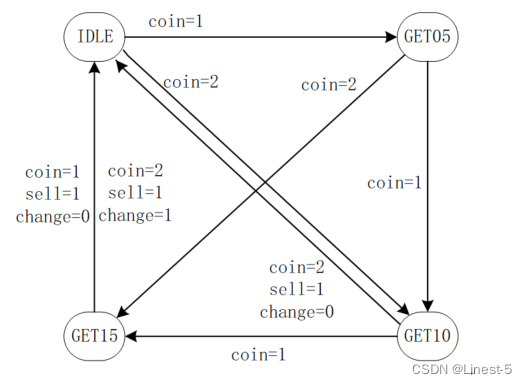
该售卖机的工作状态转移图如下所示，包含了输入、输出信号状态。

其中，coin = 1 代表投入了 0.5 元硬币，coin = 2 代表投入了 1 元硬币。

16b9290bf40f4e949775cbd17a5cb890.png

状态机设计：3 段式（推荐）

状态机设计如下：

  • (0) 首先，根据状态机的个数确定状态机编码。利用编码给状态寄存器赋值，代码可读性更好。
  • (1) 状态机第一段，时序逻辑，非阻塞赋值，传递寄存器的状态。
  • (2) 状态机第二段，组合逻辑，阻塞赋值，根据当前状态和当前输入，确定下一个状态机的状态。
  • (3) 状态机第三段，时序逻辑，非阻塞赋值，因为是 Mealy 型状态机，根据当前状态和当前输入，确定输出信号。

实例

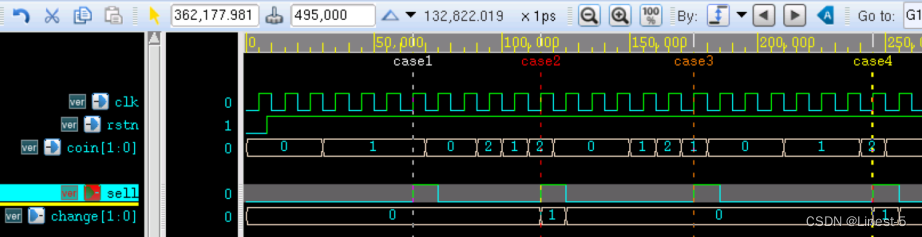
module  vending_machine_p3  (input           clk ,input           rstn ,input [1:0]     coin ,     output [1:0]    change ,     //找零output          sell         //输出饮料);//machine state decodeparameter           IDLE   = 3'd0 ;parameter           GET05  = 3'd1 ;parameter           GET10  = 3'd2 ;parameter           GET15  = 3'd3 ;reg  [2:0]          st_next ;reg  [2:0]          st_cur ;reg  [1:0]          change_r ;reg           	sell_r ;//第一段状态机，时序逻辑 非阻塞赋值always @(posedge clk or negedge rstn) beginif (!rstn) beginst_cur <= 'b0 ;endelse beginst_cur <= st_next ;endend//第二段状态机 ，组合逻辑 阻塞赋值  always @(*) beginst_next = st_cur ;        //如果条件选项考虑不全，可以赋初值消除latchcase(st_cur)IDLE:case (coin)2'b01:     st_next = GET05 ;2'b10:     st_next = GET10 ;default:   st_next = IDLE ;endcaseGET05:case (coin)2'b01:     st_next = GET10 ;2'b10:     st_next = GET15 ;default:   st_next = GET05 ;endcaseGET10:case (coin)2'b01:     st_next = GET15 ;2'b10:     st_next = IDLE ;default:   st_next = GET10 ;endcaseGET15:case (coin)2'b01,2'b10:st_next = IDLE ;default:   st_next = GET15 ;endcasedefault:  st_next = IDLE ;endcaseend//第三段状态机，时序逻辑 非阻塞赋值always @(posedge clk or negedge rstn) beginif (!rstn) beginchange_r <= 2'b0 ;sell_r   <= 1'b0 ;			endelse begincase (st_cur)IDLE:beginchange_r <= 2'b0 ;sell_r   <= 1'b0 ;endGET05:beginchange_r <= 2'b0 ;sell_r   <= 1'b0 ;endGET10:beginif (coin ==2'd2) beginchange_r <= 2'b0 ;sell_r   <= 1'b1 ;	endelse beginchange_r <= 2'b0 ;sell_r   <= 1'b0 ;endendGET15:beginif (coin ==2'h1) beginchange_r <= 2'b0 ;sell_r   <= 1'b1 ;endelse if (coin == 2'h2) beginchange_r <= 2'b1 ;sell_r   <= 1'b1 ;endelse beginchange_r <= 2'b0 ;sell_r   <= 1'b0 ;endenddefault:beginchange_r <= 2'b0 ;sell_r   <= 1'b0 ;endendcaseendendassign  sell = sell_r ;assign  change = change_r ;endmodule

testbench 设计如下。仿真中模拟了 4 种情景，分别是：

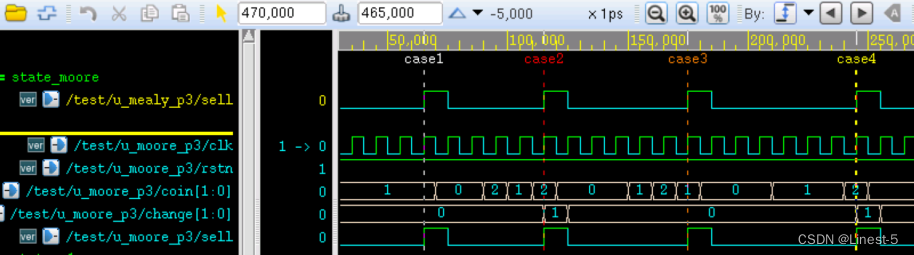
case1 对应连续输入 4 个 5 角硬币；case2 对应 1 元 - 5 角 - 1 元的投币顺序；case3 对应 5 角 - 1 元 - 5 角的投币顺序；case4 对应连续 3 个 5 角然后一个 1 元的投币顺序。

实例

`timescale 1ns/1ps
module test ;reg          clk;reg          rstn ;reg [1:0]    coin ;wire [1:0]   change ;wire         sell ;//clock generatingparameter    CYCLE_200MHz = 10 ; always beginclk = 0 ; #(CYCLE_200MHz/2) ;clk = 1 ; #(CYCLE_200MHz/2) ;end//motivation generatingreg [9:0]    buy_oper ;initial beginbuy_oper  = 'h0 ;coin      = 2'h0 ;rstn      = 1'b0 ;#8 rstn   = 1'b1 ;@(negedge clk) ;//case(1) 0.5 -> 0.5 -> 0.5 -> 0.5#16 ;buy_oper  = 10'b00_0101_0101 ;repeat(5) begin@(negedge clk) ;coin      = buy_oper[1:0] ;buy_oper  = buy_oper >> 2 ;end//case(2) 1 -> 0.5 -> 1, taking change#16 ;buy_oper  = 10'b00_0010_0110 ;repeat(5) begin@(negedge clk) ;coin      = buy_oper[1:0] ;buy_oper  = buy_oper >> 2 ;end//case(3) 0.5 -> 1 -> 0.5#16 ;buy_oper  = 10'b00_0001_1001 ;repeat(5) begin@(negedge clk) ;coin      = buy_oper[1:0] ;buy_oper  = buy_oper >> 2 ;end//case(4) 0.5 -> 0.5 -> 0.5 -> 1, taking change#16 ;buy_oper  = 10'b00_1001_0101 ;repeat(5) begin@(negedge clk) ;coin      = buy_oper[1:0] ;buy_oper  = buy_oper >> 2 ;endend//(1) mealy state with 3-stagevending_machine_p3    u_mealy_p3     (.clk              (clk),.rstn             (rstn),.coin             (coin),.change           (change),.sell             (sell));//simulation finishalways begin#100;if ($time >= 10000)  $finish ;endendmodule 

仿真结果如下:

由图可知，代表出货动作的信号 sell 都能在投币完毕后正常的拉高，而代表找零动作的信号 change 也都能根据输入的硬币场景输出正确的是否找零信号。

09ad118b0f604446ba1b9b896699c333.png

 

状态机修改：2 段式

将 3 段式状态机 2、3 段描述合并，其他部分保持不变，状态机就变成了 2 段式描述。

修改部分如下：

实例

reg  [1:0]   change_r ;
reg          sell_r ;
always @(*) begin case(st_cur)IDLE: beginchange_r     = 2'b0 ;sell_r       = 1'b0 ;case (coin)2'b01:     st_next = GET05 ;2'b10:     st_next = GET10 ;default:   st_next = IDLE ;endcase endGET05: beginchange_r     = 2'b0 ;sell_r       = 1'b0 ;case (coin)2'b01:     st_next = GET10 ;2'b10:     st_next = GET15 ;default:   st_next = GET05 ;endcase endGET10:case (coin)2'b01:     beginst_next      = GET15 ;change_r     = 2'b0 ;sell_r       = 1'b0 ;end2'b10:     beginst_next      = IDLE ;change_r     = 2'b0 ;sell_r       = 1'b1 ;enddefault:   beginst_next      = GET10 ;change_r     = 2'b0 ;sell_r       = 1'b0 ;endendcase GET15:case (coin)2'b01: beginst_next     = IDLE ;change_r    = 2'b0 ;sell_r      = 1'b1 ;end2'b10:     beginst_next     = IDLE ;change_r    = 2'b1 ;sell_r      = 1'b1 ;enddefault:   beginst_next     = GET15 ;change_r    = 2'b0 ;sell_r      = 1'b0 ;endendcasedefault:  beginst_next     = IDLE ;change_r    = 2'b0 ;sell_r      = 1'b0 ;endendcase
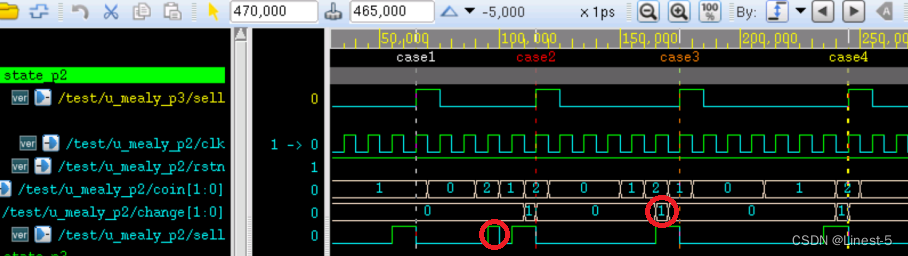
end

将上述修改的新模块例化到 3 段式的 testbench 中即可进行仿真，结果如下:

由图可知，出货信号 sell 和 找零信号 change 相对于 3 段式状态机输出提前了一个时钟周期，这是因为输出信号都是阻塞赋值导致的。

如图中红色圆圈部分，输出信号都出现了干扰脉冲，这是因为输入信号都是异步的，而且输出信号是组合逻辑输出，没有时钟驱动。

实际中，如果输入信号都是与时钟同步的，这种干扰脉冲是不会出现的。如果是异步输入信号，首先应当对信号进行同步。

494fa55d50ab4f81919543fe192e2090.png

 

状态机修改：1 段式（慎用）

将 3 段式状态机 1、 2、3 段描述合并，状态机就变成了 1 段式描述。

修改部分如下：

实例

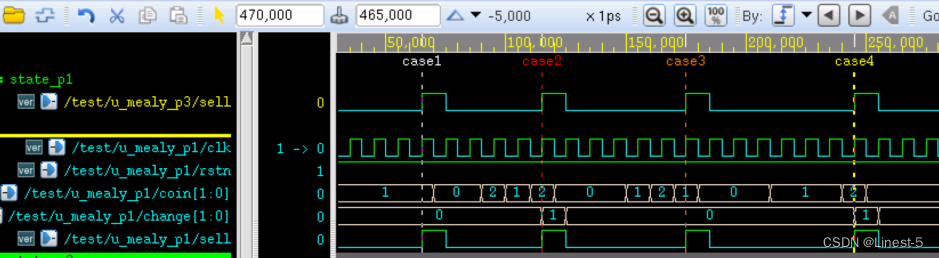
    reg  [1:0]   change_r ;reg          sell_r ;always @(posedge clk or negedge rstn) beginif (!rstn) beginst_cur     <= 'b0 ;change_r   <= 2'b0 ;sell_r     <= 1'b0 ;endelse begincase(st_cur)IDLE: beginchange_r  <= 2'b0 ;sell_r    <= 1'b0 ;case (coin)2'b01:     st_cur <= GET05 ;2'b10:     st_cur <= GET10 ;endcaseendGET05: begincase (coin)2'b01:     st_cur <= GET10 ;2'b10:     st_cur <= GET15 ;endcaseendGET10:case (coin)2'b01:     st_cur   <=  GET15 ;2'b10:     beginst_cur   <= IDLE ;sell_r   <= 1'b1 ;endendcaseGET15:case (coin)2'b01:     beginst_cur   <= IDLE ;sell_r   <= 1'b1 ;end2'b10:     beginst_cur   <= IDLE ;change_r <= 2'b1 ;sell_r   <= 1'b1 ;endendcasedefault:  beginst_cur    <= IDLE ;endendcase // case (st_cur)end end

将上述修改的新模块例化到 3 段式的 testbench 中即可进行仿真，结果如下:

由图可知，输出信号与 3 段式状态机完全一致。

1 段式状态机的缺点就是许多种逻辑糅合在一起，不易后期的维护。当状态机和输出信号较少时，可以尝试此种描述方式。

00bd7ab917b24ee0835c952a6391ea24.png

 

状态机修改：Moore 型

如果使用 Moore 型状态机描述售卖机的工作流程，那么还需要再增加 2 个状态编码，用以描述 Mealy 状态机输出时的输入信号和状态机状态。

3 段式 Moore 型状态机描述的自动售卖机 Verilog 代码如下：

实例

module  vending_machine_moore    (input           clk ,input           rstn ,input [1:0]     coin ,     output [1:0]    change ,output          sell    );parameter            IDLE   = 3'd0 ;parameter            GET05  = 3'd1 ;parameter            GET10  = 3'd2 ;parameter            GET15  = 3'd3 ;parameter            GET20  = 3'd4 ;parameter            GET25  = 3'd5 ;reg [2:0]            st_next ;reg [2:0]            st_cur ;//(1) state transferalways @(posedge clk or negedge rstn) beginif (!rstn) beginst_cur      <= 'b0 ;endelse beginst_cur      <= st_next ;endendalways @(*) begin //all case items need to be displayed completelycase(st_cur)IDLE:case (coin)2'b01:     st_next = GET05 ;2'b10:     st_next = GET10 ;default:   st_next = IDLE ;endcaseGET05:case (coin)2'b01:     st_next = GET10 ;2'b10:     st_next = GET15 ;default:   st_next = GET05 ;endcaseGET10:case (coin)2'b01:     st_next = GET15 ;2'b10:     st_next = GET20 ;default:   st_next = GET10 ;endcaseGET15:case (coin)2'b01:     st_next = GET20 ;2'b10:     st_next = GET25 ;default:   st_next = GET15 ;endcaseGET20:         st_next = IDLE ;GET25:         st_next = IDLE ;default:       st_next = IDLE ;endcaseend reg  [1:0]   change_r ;reg          sell_r ;always @(posedge clk or negedge rstn) beginif (!rstn) beginchange_r       <= 2'b0 ;sell_r         <= 1'b0 ;endelse if (st_cur == GET20 ) beginsell_r         <= 1'b1 ;endelse if (st_cur == GET25) beginchange_r       <= 2'b1 ;sell_r         <= 1'b1 ;endelse beginchange_r       <= 2'b0 ;sell_r         <= 1'b0 ;endendassign       sell    = sell_r ;assign       change  = change_r ;endmodule

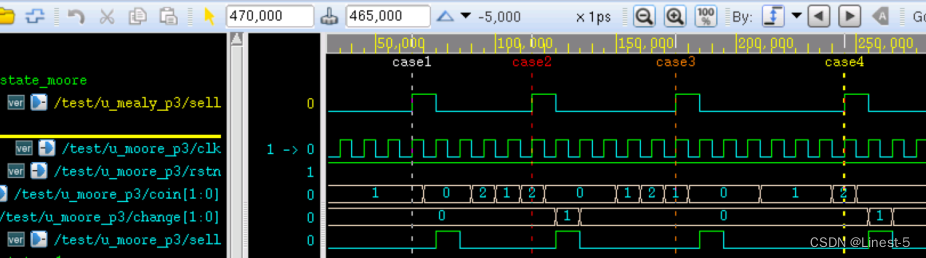
将上述修改的 Moore 状态机例化到 3 段式的 testbench 中即可进行仿真，结果如下:

由图可知，输出信号与 Mealy 型 3 段式状态机相比延迟了一个时钟周期，这是因为进入到新增加的编码状态机时需要一个时钟周期的时延。此时，输出再用非阻塞赋值就会导致最终的输出信号延迟一个时钟周期。这也属于 Moore 型状态机的特点。

6fa9cb1dd11947fda6142b40818fc4f4.png

 

输出信号赋值时，用阻塞赋值，则可以提前一个时钟周期。

输出逻辑修改如下。

实例

    reg  [1:0]   change_r ;reg          sell_r ;always @(*) beginchange_r  = 'b0 ;sell_r    = 'b0 ; //not list all condition, initializing themif (st_cur == GET20 ) beginsell_r         = 1'b1 ;endelse if (st_cur == GET25) beginchange_r       = 2'b1 ;sell_r         = 1'b1 ;endend

输出信号阻塞赋值的仿真结果如下:

由图可知，输出信号已经和 3 段式 Mealy 型状态机一致。

 

bf44371e24ea49bd8ce54a04692c768d.png

 

 


http://chatgpt.dhexx.cn/article/a3uZi5d2.shtml

相关文章

状态机的描述方法案例分析（一段式、二段式、三段式）

状态机的描述方法案例分析（一段式、二段式、三段式）

上篇博文讲了&#xff1a;FPGA中有限状态机的状态编码采用格雷码还是独热码&#xff1f; 那篇博文讲了状态机的状态编码是用格雷码还是独热码的问题&#xff0c;以及两者之间的优劣。状态机的描述方式采用的是一段式描述方式&#xff0c;也就是将整个状态机全部写到一个always…
阅读更多...
FPGA状态机（一段式、二段式、三段式）、摩尔型（Moore）和米勒型（Mealy）

FPGA状态机（一段式、二段式、三段式）、摩尔型（Moore）和米勒型（Mealy）

1、状态机 1.1、理论 FPGA不同于CPU的一点特点就是CPU是顺序执行的&#xff0c;而FPGA是同步执行&#xff08;并行&#xff09;的。那么FPGA如何处理明显具有时间上先后顺序的事件呢&#xff1f;这个时候我们就需要使用到状态机了。 状态机简写为 FSM&#xff08;Finite Sta…
阅读更多...
三段式状态机_verilog

三段式状态机_verilog

这是一篇转载的文章&#xff0c;但是个人理解笔者将前两个always块结构搞错了&#xff0c;自行纠正了一下。 原文链接 https://www.jianshu.com/p/5eee434ab24d 1. 三段式要求 有限状态机采用三段式风格&#xff0c;即三个always块描述状态机. 第一个时序逻辑always块用来描…
阅读更多...
2021-08-21Verilog三段式状态机的写法，标准示例和仿真。

2021-08-21Verilog三段式状态机的写法，标准示例和仿真。

Verilog三段式状态机的写法&#xff0c;标准示例和仿真。 第一段&#xff1a;同步状态转移。第一个always块格式化描述次态寄存器迁移到现态寄存器。 第二段&#xff1a;当前状态判断接下来的状态。组合逻辑always模块&#xff0c;描述状态转移条件判断用current_state 第三段&…
阅读更多...
verilog 3段式状态机

verilog 3段式状态机

3段式状态机&#xff1a; 3段式状态机写法&#xff0c;写出下图状态转换图。 1 确定输入输出信号&#xff0c;及其类型&#xff08;是wire还是reg&#xff09;&#xff1b; 2 声明内部信号&#xff0c;一般需要定义current_state和next_state&#xff1b; 3 用3个always语句描…
阅读更多...
三段式状态机设计

三段式状态机设计

状态机设计需满足的几个要求&#xff1a; 1. 三段式要求 有限状态机采用三段式风格&#xff0c;即三个always块描述状态机. 第一个组合逻辑always块用来描述下一状态的转移&#xff08;next state logic&#xff09; 第二个时序逻辑always块用来描述当前状态.&#xff08;cur…
阅读更多...
三段式状态机浅析

三段式状态机浅析

三段式状态机 文章目录 三段式状态机三段式状态机优点书写格式formater整形器状态机书写举例 关注作者 三段式状态机优点 将组合逻辑与时序逻辑分开&#xff0c;所写代码层次清晰&#xff0c;方便理解和后续的维护相较两段式状态机&#xff0c;解决了输出毛刺的影响。 书写格…
阅读更多...
（三段式）有限状态机【原理+实例】

（三段式）有限状态机【原理+实例】

状态机的基本要素&#xff1a;输入、输出、状态。 状态机根据状态变化是否与输入条件有关分为两类&#xff1a;即Moore型状态机和Mealy型状态机。 Moore型状态机的状态变化仅和当前状态有关&#xff0c;而与输入条件无关&#xff1b; Mealy型状态机的状态变化不仅和当前状态…
阅读更多...
状态机设计(一段式、两段式和三段式)

状态机设计(一段式、两段式和三段式)

三段式状态机 第一段&#xff0c;时序always块&#xff0c;状态跳转 第二段&#xff0c;组合always块&#xff0c;状态更新 第三段&#xff0c;时序always块&#xff0c;输出控制 两段式状态机 两段式状态机是把三段式状态机的第二段和第三段合为一段&#xff0c;那么两段式…
阅读更多...
FPGA——三段式状态机(1)

FPGA——三段式状态机(1)

状态机全称是有限状态机&#xff08;Finite State Machine、FSM&#xff09;&#xff0c;是表示有限个状态以及在这些状态之间的转移和动作等行为的数学模型。状态机可根据控制信号完成预定的状态转换&#xff0c;由组合逻辑电路和寄存器组成&#xff0c;可由状态转换表或状态转…
阅读更多...
状态机详解（一段式、二段式、三段式）

状态机详解（一段式、二段式、三段式）

一、有限状态机FSM&#xff08;Finite State Machine&#xff09; 组成元素&#xff1a; 输入、状态、状态转移条件、输出。 可以分为两类&#xff1a; Mealy状态机&#xff1a;时序逻辑的输出不仅取决于当前状态&#xff0c;还与输入有关&#xff1b; Moore状态机&#xff1a…
阅读更多...
三段式状态机理解浅析

三段式状态机理解浅析

版权声明&#xff1a;本文为博主原创文章&#xff0c;遵循 CC 4.0 BY-SA 版权协议&#xff0c;转载请附上原文出处链接和本声明。 本文链接&#xff1a;https://blog.csdn.net/weixin_43070186/article/details/82085463 关于FSM的写法按照always块的个数来划分可以分为一段式…
阅读更多...
彻底搞懂状态机（一段式、两段式、三段式）

彻底搞懂状态机（一段式、两段式、三段式）

转自&#xff1a;https://blog.csdn.net/wordwarwordwar/article/details/78509445 实例&#xff1a;FSM实现10010串的检测 状态转移图&#xff1a;初始状态S0&#xff0c;a 0,z 0.如果检测到1&#xff0c;跳转到S1。 下一状态S1&#xff0c;a 1,z 0.如果检测到0&#xff…
阅读更多...
Verilog：三段式状态机（数字钟）

Verilog：三段式状态机（数字钟）

状态机在FPGA的设计中是至关重要的&#xff0c;使用的频率也很高&#xff0c;废话不多说在这里介绍一下三段式状态机如何设计。 设计状态机首先要清楚状态有几种&#xff0c;状态转移图是怎样的&#xff0c;各个状态的输出是怎样的。了解了这三样之后就可以开始设计实验所需要的…
阅读更多...
三段式有限状态机

三段式有限状态机

一段式、二段式、三段式状态机是按照书写FSM时使用的always块数目进行划分的&#xff0c;一般而言对于简单的状态机&#xff0c;可以使用一段式&#xff0c;其代码量以及使用资源都最少&#xff0c;但如果状态机较复杂&#xff0c;一段式状态机会对代码维护产生很大的不便&…
阅读更多...
状态机，从细节出发（一段式、两段式、三段式，moore型、mealy型）

状态机，从细节出发（一段式、两段式、三段式，moore型、mealy型）

目录 前言 一、状态机要素 二、状态机描述方法 1、一段式描述方法 2、两段式描述方法 3、三段式描述方法 三、关系 1、一段式与三段式 2、两段式与三段式 3、三种FSM描述方法比较表 四、状态机的种类 1、Moore型状态机 2、Mealy型状态机 3、注意点 五、举例 1、…
阅读更多...
时间复杂度与空间复杂度分析（递归与非递归比较）

时间复杂度与空间复杂度分析（递归与非递归比较）

时间复杂度&#xff1a; 一般情况下&#xff0c;算法中基本操作重复的次数就是问题规模n的某个函数f&#xff08;n&#xff09;&#xff0c;进而分析f&#xff08;n&#xff09;随n的变化情况并确定T&#xff08;n&#xff09;的数量级。这里用‘o’来表示数量级&#xff0c;给…
阅读更多...
数据结构：时间复杂度空间复杂度(递归)

数据结构：时间复杂度空间复杂度(递归)

转载文章 时间复杂度&#xff1a; 一般情况下&#xff0c;算法中基本操作重复执行的次数是问题规模n的某个函数f(n)&#xff0c;进而分析f(n)随n的变化情况并确定T(n)的数量级。这里用"O"来表示数量级&#xff0c;给出算法的时间复杂度。 T(n)O(f(n)); 它表示随着问…
阅读更多...
递归理解以及时间复杂度计算

递归理解以及时间复杂度计算

一.复杂度分析&#xff1a; 可以理解为递归的深度就是空间复杂度&#xff0c;时间复杂度就是O(T*depth),其中&#xff34;是每个递归函数的时间复杂度&#xff0c;depth是递归深度&#xff0e; #空间复杂度O(1) def sum1_(n):res 0for i in range(n1):resireturn res#递归 空…
阅读更多...
递归的时间与空间复杂度

递归的时间与空间复杂度

一、 递归的时间复杂度 递归算法的时间复杂度 递归次数 \times 每次递归的时间复杂度。 递归次数&#xff1a;可以通过画递归树&#xff0c;数递归树的节点数&#xff0c;得到递归次数。 二、递归的空间复杂度 递归算法的空间复杂度 递归深度 \times 每次入栈的空间…
阅读更多...
推荐文章

Copyright @ 2022~2023