时间复杂度与空间复杂度分析（递归与非递归比较）

article/2025/9/20 0:16:31

时间复杂度：
一般情况下，算法中基本操作重复的次数就是问题规模n的某个函数f（n），进而分析f（n）随n的变化情况并确定T（n）的数量级。这里用‘o’来表示数量级，给出算法时间复杂度。
T（n）=o（f（n））；
它表示随问题规模n的增大，算法的执行时间增长率和f（n）增长率成正比，这称作算法的渐进时间复杂度。而我们一般情况下讨论的最坏的时间复杂度。
空间复杂度：
算法的空间复杂度并不是实际占用的空间，而是计算整个算法空间辅助空间单元的个数，与问题的规模没有关系。算法的空间复杂度S（n）定义为该算法所耗费空间的数量级。
S（n）=o（f（n））
若算法执行所需要的辅助空间相对于输入数据n而言是一个常数，则称这个算法空间复杂度辅助空间为o（1）；
递归算法空间复杂度：递归深度n*每次递归所要的辅助空间，如果每次递归所需要的辅助空间为常数，则递归空间复杂度o（n）。

int binary_search(int *a,int size,int value)  //[left,right);
{int left = 0;int right = size;while (left < right){int mid = left + ((right - left) >> 1);if (value > a[mid])left = mid + 1;else if (value < a[mid])right = mid ;elsereturn mid;}return -1;
}
int binary_search1(int *a, int size, int value)//[left,right]
{int left = 0;int right = size - 1;while (left <= right){int mid = left + ((right - left) >> 1);if (value > a[mid])left = mid + 1;else if (value < a[mid])right = mid - 1;elsereturn mid;}return -1;
}

折半查找时间复杂度：

这里写图片描述

假设在n个数中查找，查找第一次个数变为n/2，查找第二次个数变为（n/2）/2 依次类推计算第n次时查找的数列长度为（n/(2^x)）。设x为查找的次数，最坏情况下查找x次找到（n/(2^x)）=1
所以查找在n个数查找查找的次数为：x=log n 时间复杂度为：O（log n）(以2为底n的对数)
空间复杂度：O（1）

//递归实现二分查找
int binary_search2(int *a, int left,int right, int value)
{if (left <= right){int mid = left + ((right - left) >> 1);if (value == a[mid]){return mid;}else if (value > a[mid]){left = mid + 1;return  binary_search2(a, left, right, value);}else{right = mid - 1;return binary_search2(a, left, right, value);}}elsereturn -1;
}

int fibonacci(int a)
{if (a < 2)return a;elsereturn fibonacci(a - 1) + fibonacci(a - 2); 
}

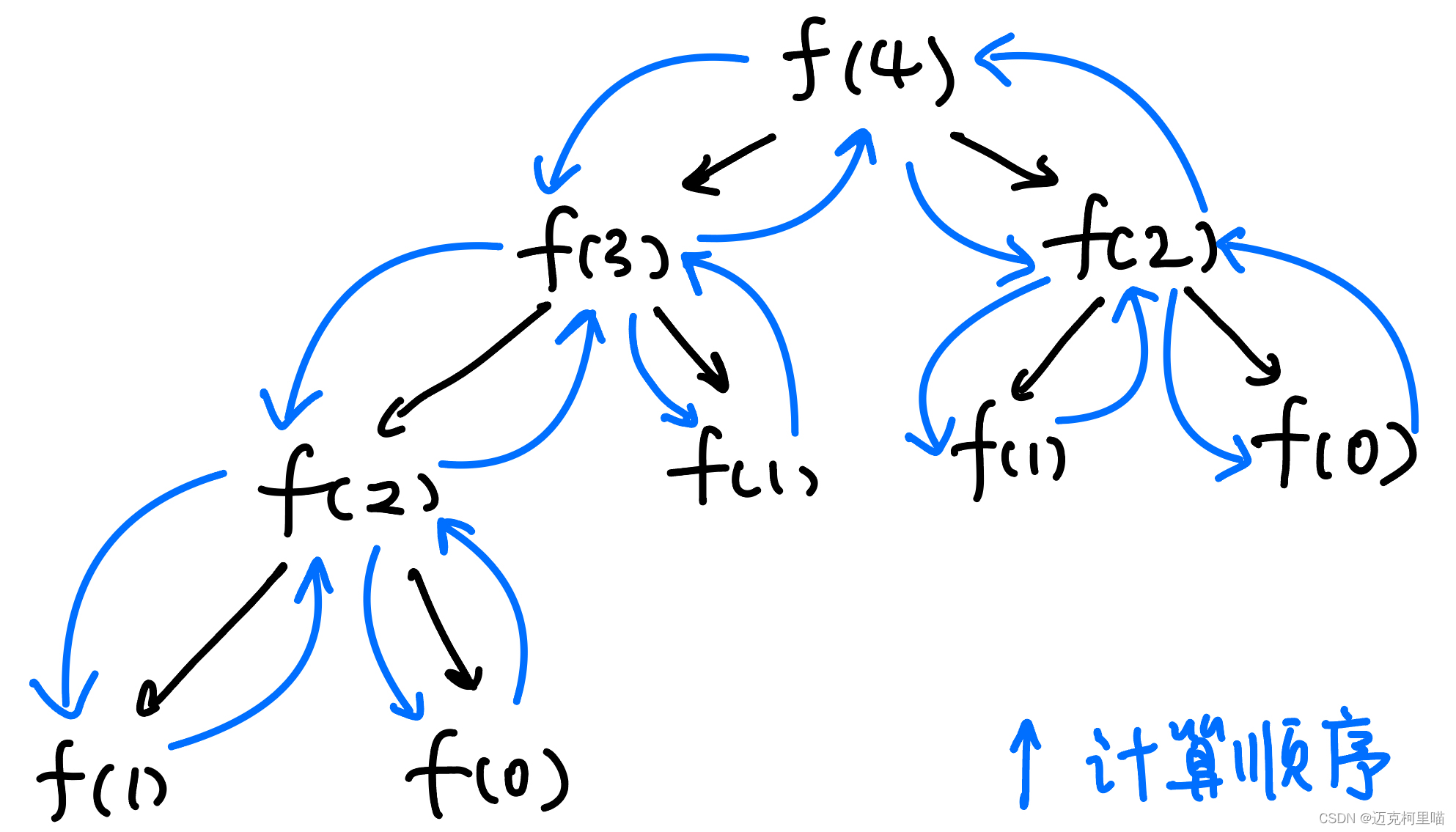
斐波那契的（递归）时间复杂度分析：

这里写图片描述

如图为递归的次数。2^5-16，以此类推，计算第n个斐波那契数是时间复杂度为O（2^n）-O(1)
即时间复杂度为 O（2^n）
空间复杂度：递归深度*每次递归所需要的辅助空间所以空间复杂度有为o（n）；

//斐波那契数的非递归算法：
int fibonacci1(int a)
{int x=0, y=1, z;if (a < 2)            return a;else{int i = 0;for (i = 2; i <= a; i++)    {                    z = x + y; x = y;y = z;}}return z;
}