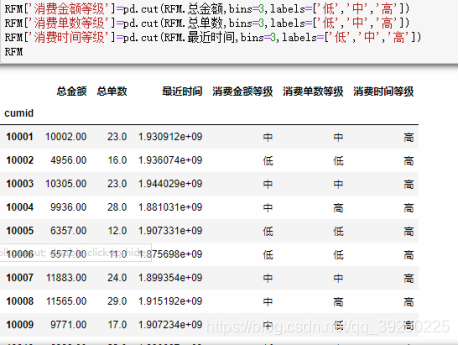
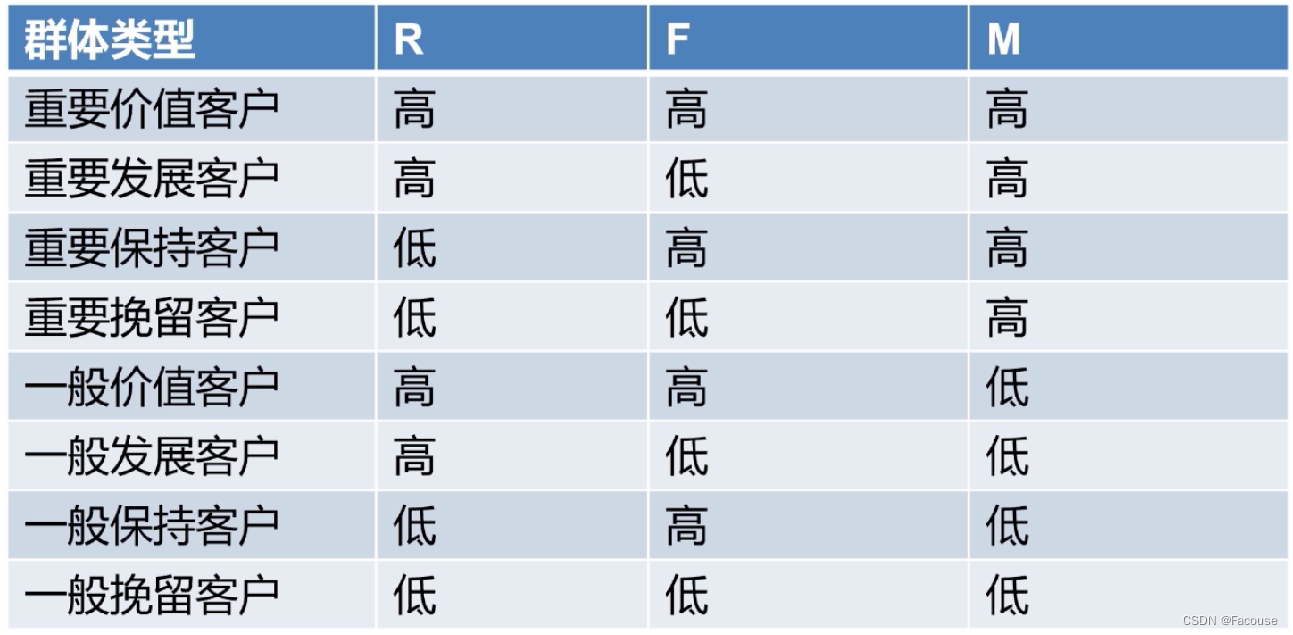
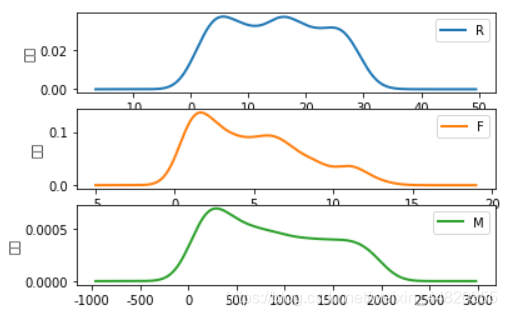
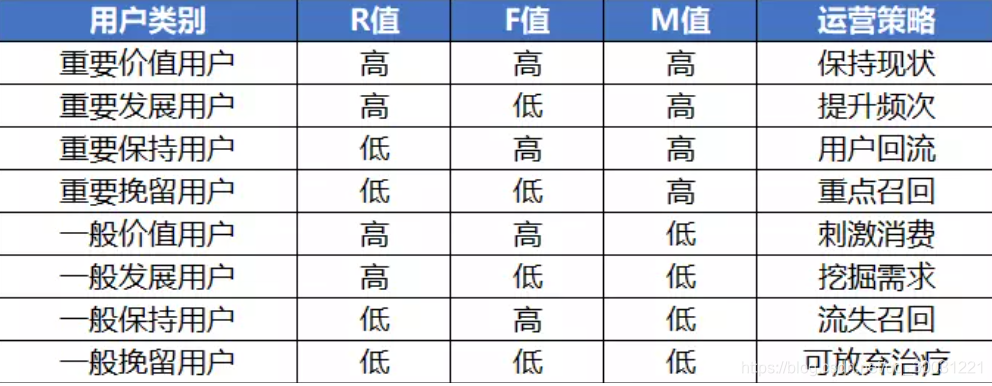
描述
给定一个由'0'和'1'组成的2维矩阵,返回该矩阵中最大的由'1'组成的正方形的面积,输入的矩阵是字符形式而非数字形式。
数据范围:矩阵的长宽满足 0 \le n \le 200≤n≤20,矩阵中的元素属于 {'1','0'}
进阶:空间复杂度 O(n^2)O(n2) , 时间复杂度 O(n^2)O(n2)
示例1
输入:[[1,0,1,0,0],[1,0,1,1,1],[1,1,1,1,1],[1,0,0,1,0]]
返回值:4
示例2
输入:[[1,0,0],[0,0,0],[0,0,0]]
返回值:1
动态规划解决
这题让求的是由1围成的最大正方形,最容易想到的一种方式就是暴力求解。解决方式就是如果某个位置是1,就以他为正方形左上角,然后沿着右边和下边找最大的正方形,并且还要保证围成的正方形中所有的数字都是1。
这种虽然容易想到但代码不太好写,并且时间复杂度也比较高。下面我们来看另一种实现方式,使用动态规划来解决。
定义二维数组dp[m][n],其中dp[i][j]表示的是在矩阵中以坐标(i,j)为右下角的最大正方形边长。如果我们想求dp[i][j],需要判断矩阵中matrix[i][j]的值。
如果matrix[i][j]是0就没法构成正方形,所以dp[i][j]=0。
如果matrix[i][j]是1,说明他可以构成一个正方形,并且这个正方形的边长最小是1。
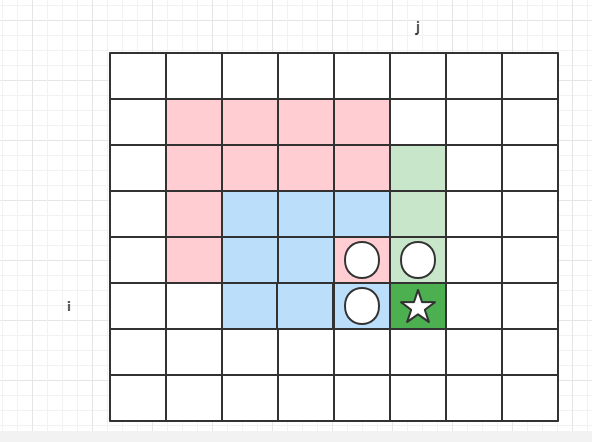
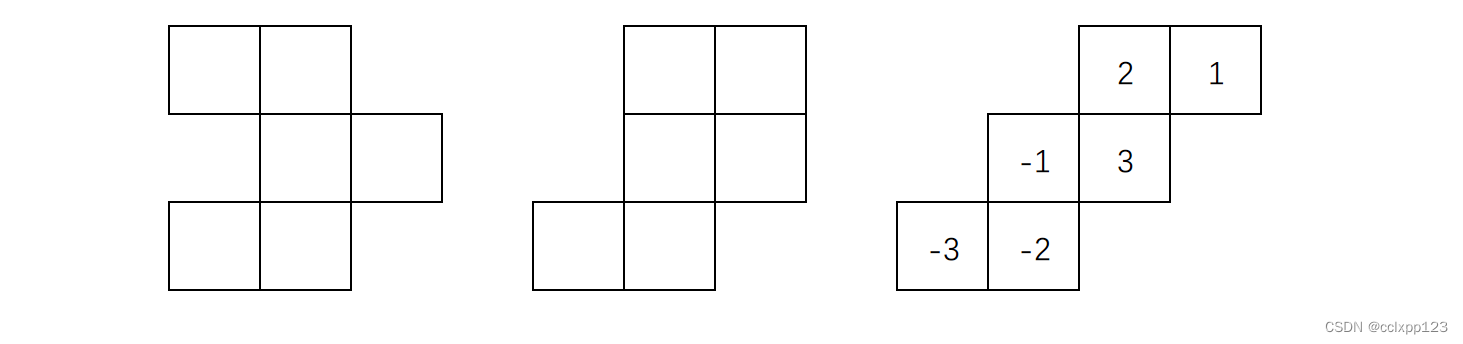
- 如果我们想求最大值,还需要判断他左上角的值dp[i-1][j-1],如果dp[i-1][j-1]是0,那么以坐标(i,j)为右下角的最大正方形边长就是1,如下图所示
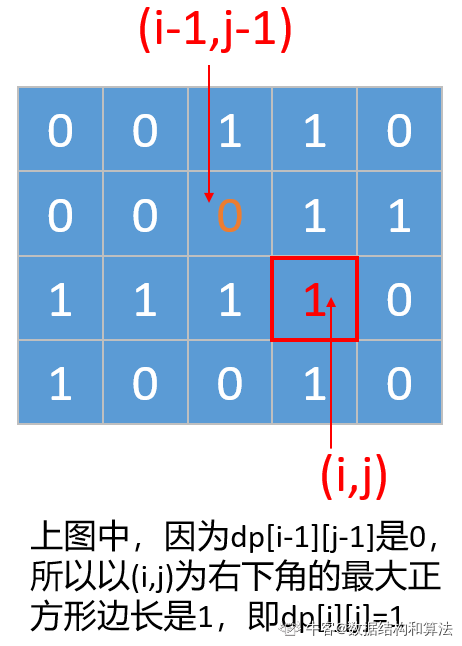
- 如果左上角的值dp[i-1][j-1]不是0,也就是说他也可以构成正方形,那么以坐标(i,j)为右下角有可能可以构成一个更大的正方形。为啥说是有可能,因为如果我们要确定他能不能构成一个更大的正方形,还要往他的上边和左边找,看下下面的图。
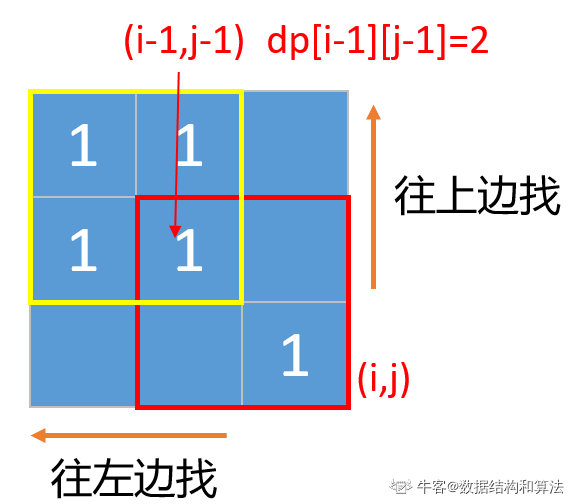
有可能是下面这种情况,就是左边或者上边的某一个高度小于dp[i-1][j-1]的值,要想构成最大的正方形我们只能取最小的。
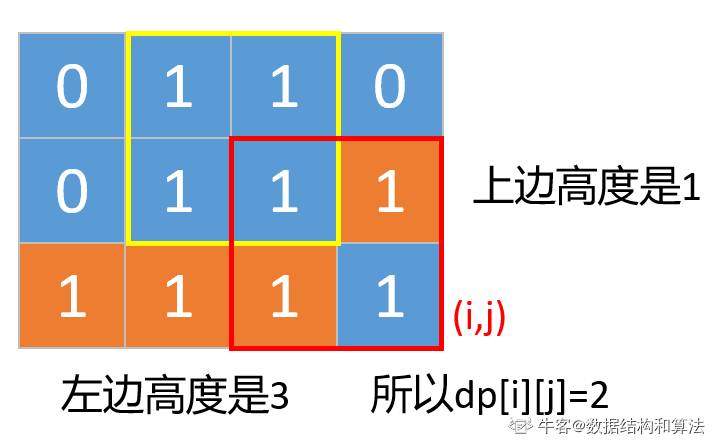
也有可能是下面这种,就是左边和上边的高度都不小于dp[i-1][j-1]的值。
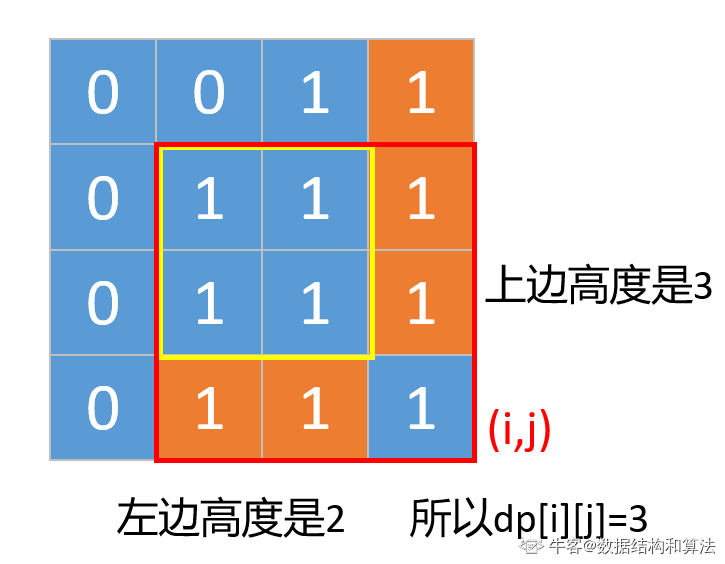
所以我们可以得出结论,如果(i,j)是1,那么以他为右下角的最大正方形边长是
{dp[i-1][j-1],上边的高度,左边的高度}这3个中最小的+1。
这里有个问题就是,如果(i,j)是1,我们有必要往他的上边和左边查找吗,很明显没必要,上边可以用dp[i-1][j]来代表,左边可以用dp[i][j-1]来代表。(注意这里dp[i-1][j]并不是上边为1的高度,dp[i-1][j]只会小,不会大,可以想一下为什么可以代表)
所以我们可以找出递推公式
如果坐标(i,j)为0,
则dp[i][j]=0;
如果坐标(i,j)为1,
则dp[i][j]=min(dp[i-1][j],dp[i][j-1],dp[i-1][j-1])+1;
为了防止一些不必要的边界条件判断,我把dp数组的长和宽都增加了1,来看下代码:
class Solution {
public:/*** 最大正方形* @param matrix char字符型vector<vector<>> * @return int整型*/int solve(vector<vector<char> >& matrix) {// write code hereif(matrix.empty()){return 0;}int m = matrix.size();int n = matrix[0].size();vector<vector<int>> dp(m+1, vector<int>(n + 1));int maxSide = 0;//最大正方形的宽for(int i = 1;i <= m; i++){for(int j = 0; j <= n; j++){if(matrix[i - 1][j - 1] == '1'){//递推公式dp[i][j] = min(dp[i-1][j], min(dp[i -1][j - 1], dp[i][j - 1])) + 1;//记录最大的边长maxSide = max(maxSide, dp[i][j]);}}}//返回正方形的面积return maxSide * maxSide;}
}