正方体的对称性

观察一个正方体的6个面. 这6个面对于正方体来说是对称的, 这里的对称并非几何或视觉上的对称, 而是一种抽象的对称. 换句话说, 为了研究正方体面的性质, 我们可以任意选择一个面, 对于这个指定面的研究结果, 可以复制到其他5个面上. 因为在指定某一个面之前, 这6个面是不可区分的. 点和线也是同样的道理.

什么是展开? 展开意味着你可以剪开某些棱, 但不能剪断所有棱, 使得某个面与整体分开, 也不能让两个面只有一个点相连, 这就是游戏规则. 规则过松或者过紧, 都会使得游戏变得无聊.

1.相对与相邻

1.1面的两种位置关系

任意指定一个面, 观察剩下的5个面与它的邻接关系. 我们发现只有两种情况: 周围的4个与它相邻, 剩下的一个与它相对. 由于前面所说的对称性, 这个结论对于其他5个面也是成立的. 因此我们得知, 正方体的面只有两种关系: 相邻和相对.

1.2展开图中的对面

任意指定一对具有相对关系的面, 称这对面为对面, 例如下图中的1和2, 3和4, 5和6都是对面. 那么对面在展开图中会有那些情况？
在这里插入图片描述

由于游戏规则中给出展开图必须是连续的. 因此这个问题可以被转化为另一个问题: 从一个面走到它的对面, 有几种不同的路径?

我们以1和2为例, 那么从1走到2有多少情况？最简单的就是从1开始, 经过4, 然后到2, 简记为142. 此外132, 162, 152这些对称的路径也都是可以的. 他们都有一个共同的特征, 从一个面开始, 经过一个侧面后直接到达对面. 这种路径在展开图中只能是排成一排的三个正方形.
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-9nzkXo1p-1660271358094)(image-20220810150313422.png)]
另外也可以经过侧面时"拐一步". 比如从1到4后, 向6拐一步, 然后下到2, 记为1462. 此外路径1632, 1352, 1542也是类似的. 这些路径在展开图中也包含"拐一步"的感觉, 形成一个Z字形.
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-mcX3BgvR-1660271358095)(image-20220810145948940.png)]
当然可以"拐两步", 形成的路径是14632. 其它就不写了. 它们在展开图也是Z字形, 但中间长一点.
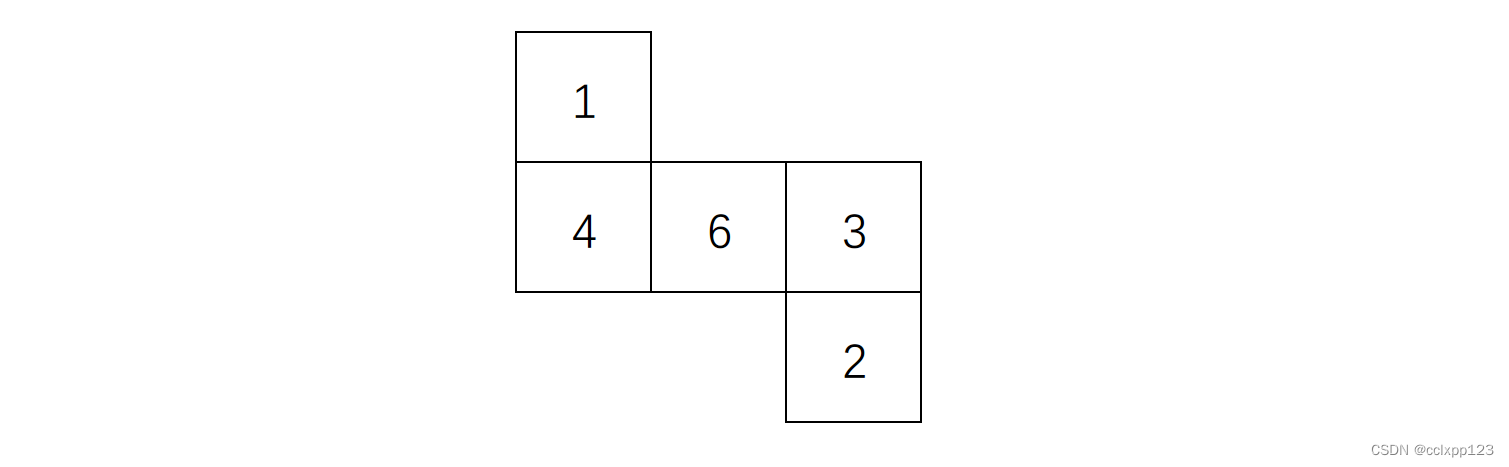
在这里插入图片描述
还可以"拐三步", 路径是146352, 展开图中是一个更长的Z字.

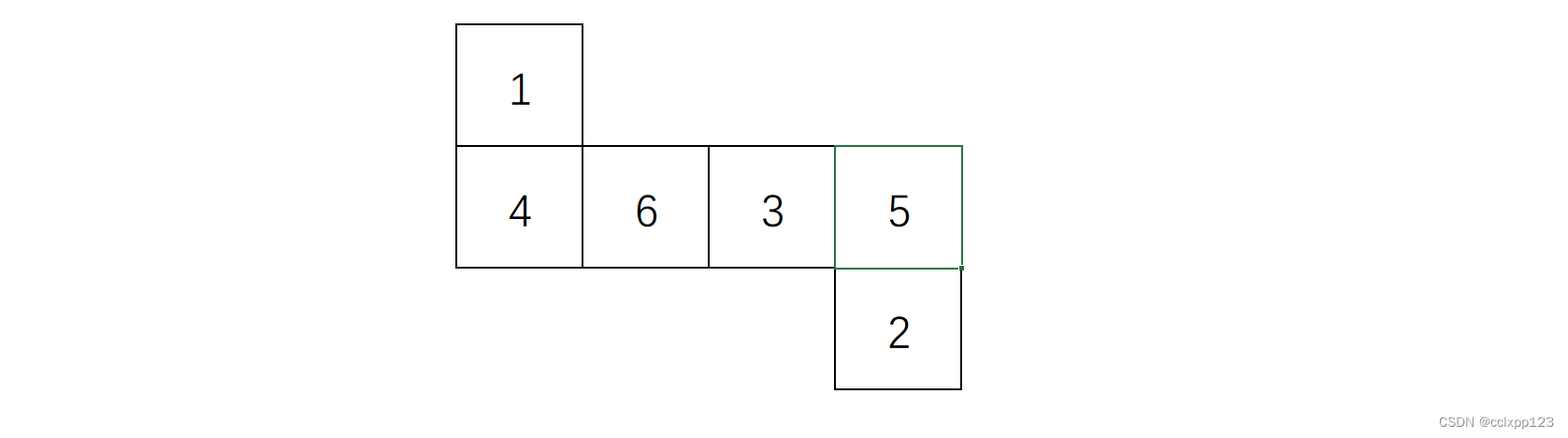
可以拐四步吗? 实际上拐四步相当于转了一圈, 回到了原来的位置, 发生了重复, 而展开图中的面都是不重复的, 因此拐四步和更多的步都是没必要的. 此外, 任何"倒退"的路径如14642也都包含了重复, 不可能包含在展开图中.

1.3小结

正方体展开图中, 对于给定的一个面, 他只有一个对面, 剩下的所有面都与它相邻. 对面的情况只有4种. 如果我们把最开始连续三个的情况看做Z字"拐0次", 那么展开图中的对面就总结为: Z字拐0~3次. 如下图色块.
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-nOUJhFIS-1660271358098)(image-20220810172434723.png)]

2.正方体的展开图

2.1问题转化

正方体的展开图有哪些可能? 我们把这个问题转化为: 给定6个正方形, 如何拼接, 才能使得拼接后的图形正确的折叠为一个正方体. 对面是唯一的, 一个正确的展开图必然包含着三对对面, 既不会重复, 也不会找不到. 展开与折叠的过程是可逆的, 因此逆问题成立, 则原问题也成立.

拼接问题是一个组合问题, 我们使用穷举的方法查看所有组合的可能, 并把正确的组合保留下来. 你可以找6片正方形的纸来试验一下.

2.2穷举组合

6=6+0

这个式子的意思是将6个正方形排成一排. 很显然这样的图形不能被折叠成正方体. 只能是一个无底无顶的六棱柱.

6=5+1

减少一个, 将5个排成一排, 同样无法折叠.

6=4+2

通过上面的测试, 发现正方体展开图最长只能是4个. 我们就构造4个, 再把剩下的2个组合在这4个上下两面(左右不行, 会把4变成5或6). 这2个还可以拆分.

2=2+0. 即把2个放在4个上面(下面和上面是对称的), 从左往右如下图

我们利用对面特征来分析. 对于三个图, 2都既是1的对面, 又是3的对面, 由于一个面的对面只有一个, 因此1和3必然重叠. 因此全部出现矛盾, 均不可能出现. 如果将上面的两个继续右移, 则与这几个图对称, 不再讨论.
如果两个方块竖直摆放, 则情况如下

同样出现了两个对面, 因此不可能. 继续右移也是对称的.
2=1+1. 则4个方块两侧各有一个, 相当于在4个位置选择2个位置, 我们可以按住一个不动, 让另一个跑动. 排除对称性, 所有情况如下

这6种情况都是可能的, 没有出现矛盾. 我们可以理解为: 用4个围成一圈, 上下的底和顶各自任意找一个位置连上即可.

6=3+3

也就是中间放三个, 剩下的三个分布在两侧. 剩下的三个也可以组合为如下情况

3=3+0. 都放在同一侧, 去除对称有三种情况
对于左图, 我们用三对相反数(1, -1), (2, -2), (3, -3)标注了对面, 没有出现矛盾. 右边两个图均出现了之前见过的"田"字, 因此去除.
3=1+2. 一边放一个, 一边放两个. 如果这两个是横着放, 排除对称有下面6种可能

除了三个明显矛盾的"田"字外, 均不出现矛盾.
如果两个竖着放, 情况如下

有两种允许的可能, 不过都与之前出现的情况重复了.

另外也可以将1和2摆在3的同一侧, 均出现重复和矛盾, 不再一一列举.

6=2+4

中间摆两个, 其它4个放在两边. 这4个只能被分解为2+2, 因为如果大于2, 就能被归位上面几种类型. 去除对称后的情况如下
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-dRyzxoNu-1660271358109)(image-20220810164648603.png)]