1.RFM的重要意义
RFM模型是衡量用户价值和用户创利能力的重要工具和手段
通过用户的近期交易行为、交易频次以及交易金额三个指标描述客户价值
| 指标 | 解释 | 意义 |
| R(Recency) | 用户最近一次交易的时间间隔 | R值越大,表示越久没有发生交易 |
| F(Frequency) | 用户在最近一段时间内的交易频次 | F值越大,表示交易越频繁 |
| M(Monetary) | 用户在最近一段时间内的交易金额 | M值越大,表示交易金额越大 |
2.RFM的计算逻辑
R分为两类,分值高为1,分值低为0;
F分为两类,分值高为1,分值低为0;
M分为两类,分值高为1,分值低为0;
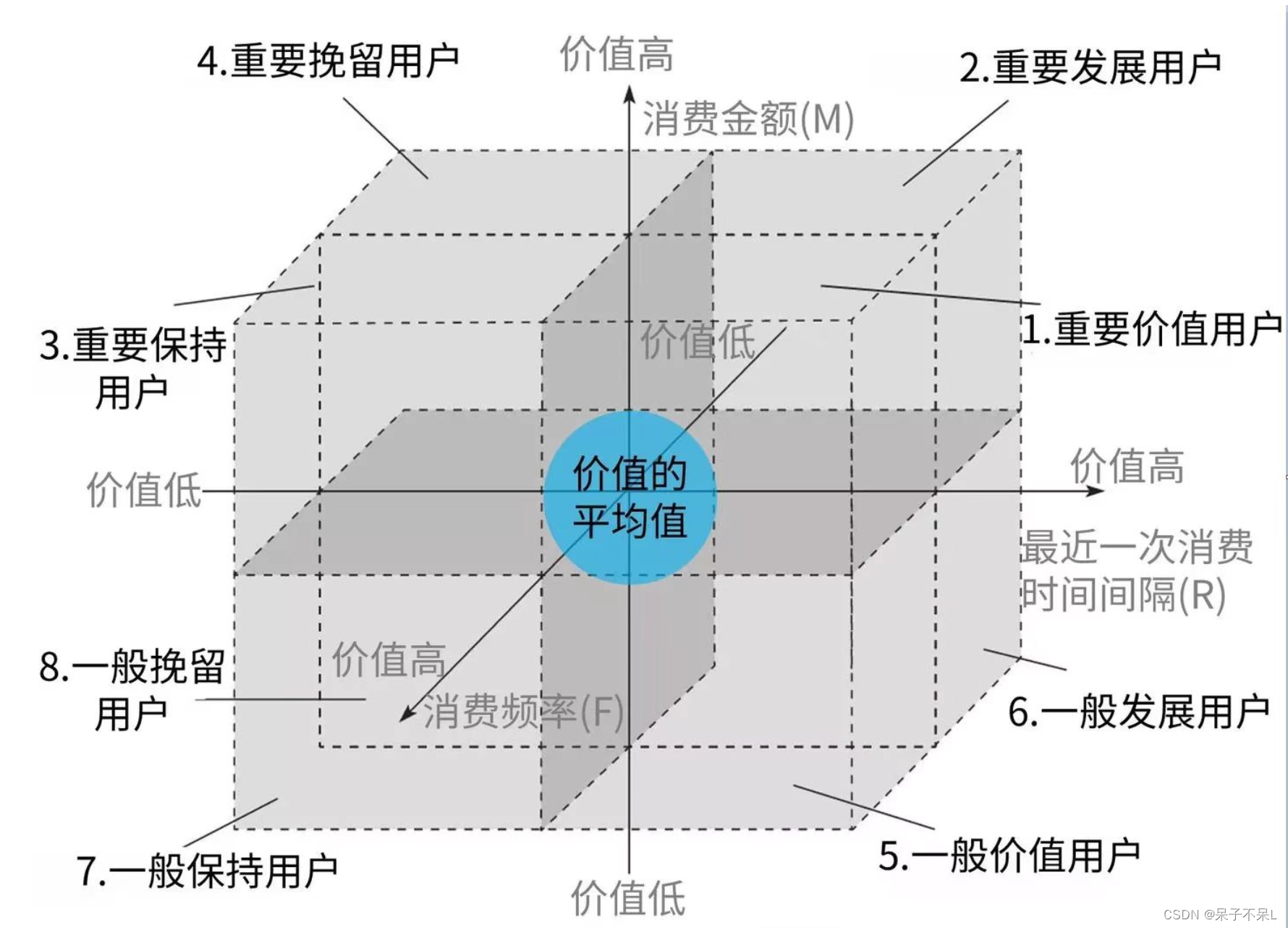
R、F和M两两组合,可得出8个不同的RFM值
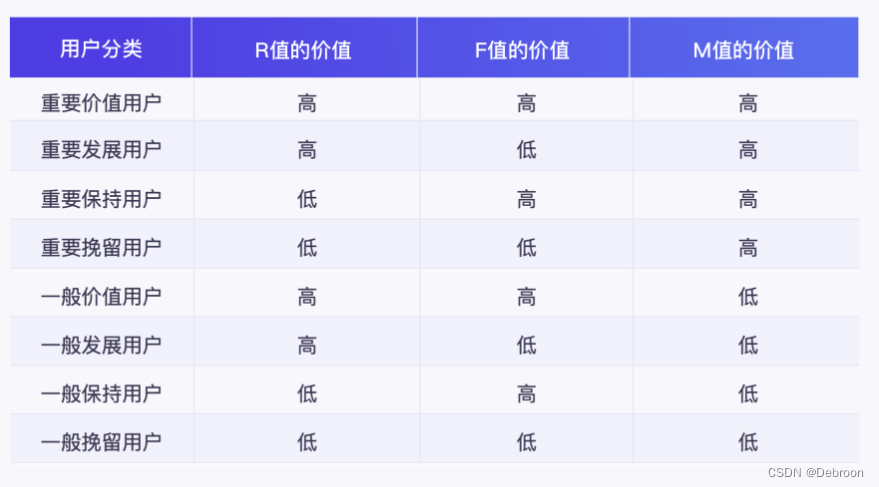
按照实际情况分为八大客户群体,具体分类规则如下:
| 用户标签 | RFM值 | 用户特点 |
| 重要价值 | 111 | 最近一次消费时间近,消费频率高,消费金额高 |
| 一般价值 | 110 | 最近一次消费时间近,消费频率高,消费金额低 |
| 重要发展 | 101 | 最近一次消费时间近,消费频率低,消费金额高 |
| 一般发展 | 100 | 最近一次消费时间近,消费频率低,消费金额低 |
| 重要保持 | 11 | 最近一次消费时间远,消费频率高,消费金额高 |
| 一般保持 | 10 | 最近一次消费时间远,消费频率高,消费金额低 |
| 重要挽留 | 1 | 最近一次消费时间远,消费频率低,消费金额高 |
| 一般挽留 | 0 | 最近一次消费时间远,消费频率低,消费金额低 |
3.例题
编辑器:jupyter notebook
import numpy as np
import pandas as pd# 读取数据
df = pd.read_excel('./data/订单明细.xlsx')
df.head()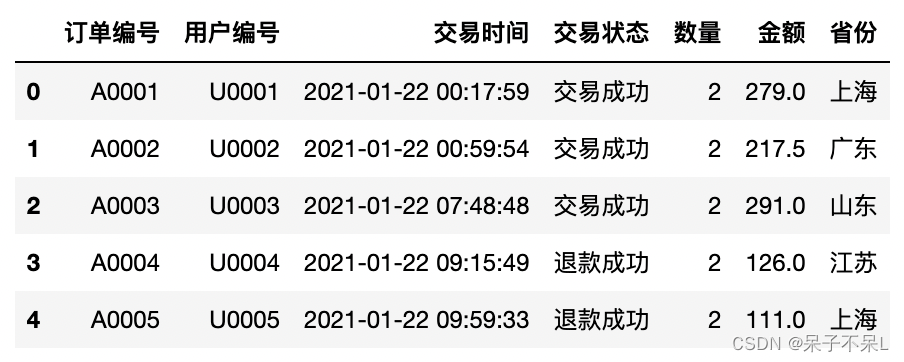
df.info()
'''
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 28832 entries, 0 to 28831
Data columns (total 7 columns):# Column Non-Null Count Dtype
--- ------ -------------- ----- 0 订单编号 28832 non-null object 1 用户编号 28832 non-null object 2 交易时间 28832 non-null datetime64[ns]3 交易状态 28832 non-null object 4 数量 28832 non-null int64 5 金额 28832 non-null float64 6 省份 28832 non-null object
dtypes: datetime64[ns](1), float64(1), int64(1), object(4)
memory usage: 1.5+ MB
'''df['交易状态'].unique()
'''
array(['交易成功', '退款成功'], dtype=object)
'''df = df[df['交易状态'] == '交易成功']
df = df[['用户编号','交易时间','金额']]
df.head()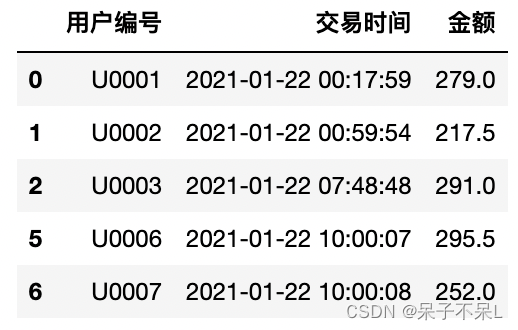
# R: 最近一次交易距今的天数
today = pd.to_datetime('2021-07-21') # 统计的时间
df_r = df.groupby('用户编号')['交易时间'].max().reset_index() # 每个用户的最近交易时间
df_r['R'] = (today - df_r['交易时间']).dt.days
df_r = df_r[['用户编号','R']]
df_r.head()
# F: 交易频次,当天多次交易仅计算一次
df['交易日期'] = df['交易时间'].dt.date
tb = df.drop_duplicates(subset=['用户编号','交易日期']) # 去重
# 以用户编号分组计数
df_f = tb.groupby('用户编号').agg(F=('用户编号','count')).reset_index()
df_f.head()
# M: 交易金额
df_m = df.groupby('用户编号').agg(M=('金额','sum')).reset_index()
df_m.head()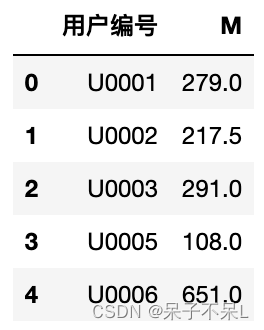
# RFM 合并(df_r/df_f/df_m三表合并)
# join\merge\concat
rfm = df_r.merge(df_f,on='用户编号').merge(df_m,on='用户编号')
rfm.head()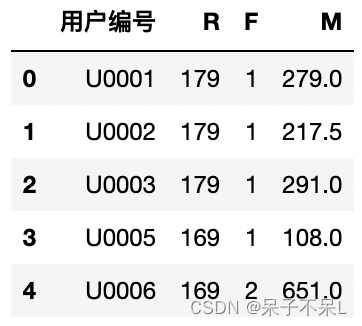
# 如果极端值过多可取中位数
# R指标的均值
avg_r = rfm['R'].mean()
# F指标的均值
avg_f = rfm['F'].mean()
# M指标的均值
avg_m = rfm['M'].mean()# R指标的分值
rfm['R_score'] = (rfm['R'] < avg_r) * 100 # 100用于做分类,也可用其他值
# F指标的分值
rfm['F_score'] = (rfm['F'] > avg_f) * 10
# M指标的分值
rfm['M_score'] = (rfm['M'] > avg_m) * 1rfm.head()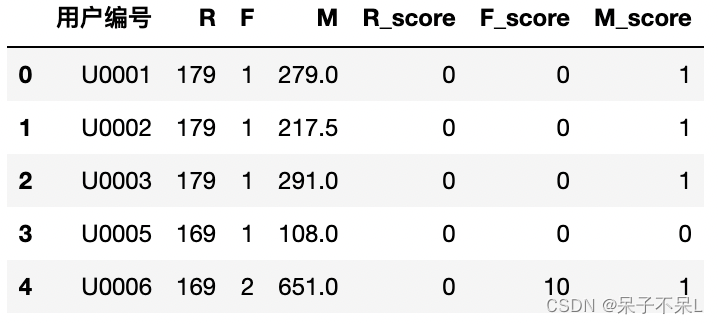
# 总分值
rfm['Total_score'] = rfm['R_score'] + rfm['F_score'] + rfm['M_score']
rfm.head()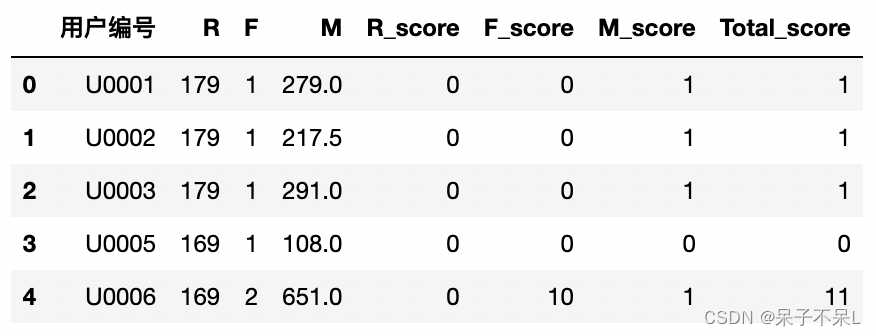
rfm['Total_score'].unique()
'''
array([ 1, 0, 11, 111, 100, 10, 110, 101])
'''dct = {111:'重要价值',110:'一般价值',101:'重要发展',100:'一般发展',11:'重要保持',10:'一般保持',1:'重要挽留',0:'一般挽留'
}
rfm['用户标签'] = rfm['Total_score'].map(dct)
rfm.head()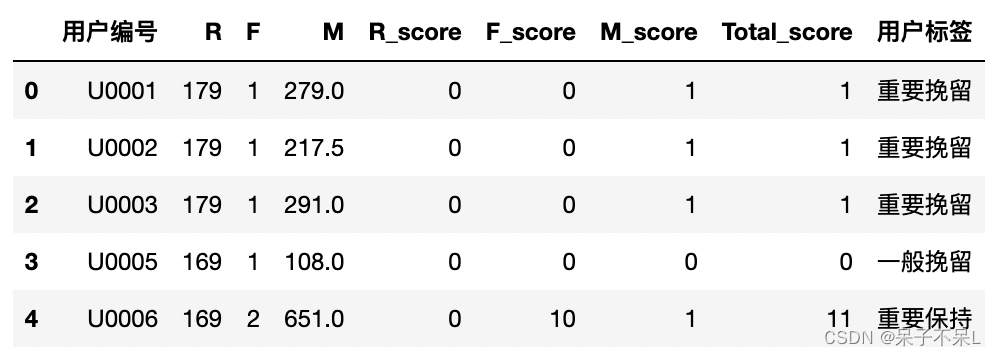
rfm['用户标签'].unique()
‘’‘
array(['重要挽留', '一般挽留', '重要保持', '重要价值', '一般发展', '一般保持', '一般价值', '重要发展'],dtype=object)
’‘’# 各类用户的人数统计
cnt = rfm['用户标签'].value_counts().reset_index()
cnt.columns = ['用户标签','人数']
cnt['人数占比'] = cnt['人数'] / cnt['人数'].sum()
cnt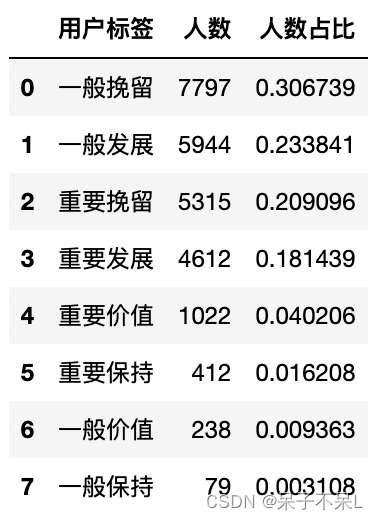
# 各类用户的金额统计
rfm['金额'] = rfm['M']
amt = rfm.groupby('用户标签')['金额'].sum().reset_index()
amt['金额占比'] = amt['金额'] / amt['金额'].sum()
amt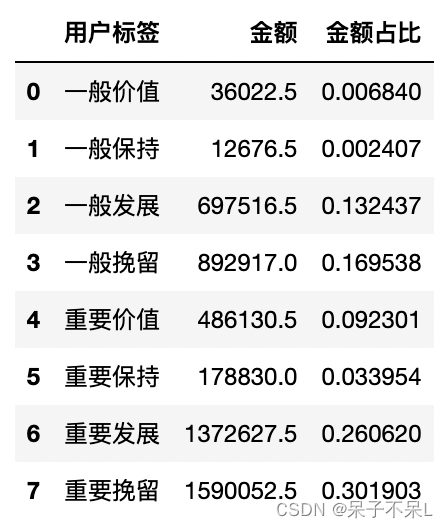
result = pd.merge(cnt,amt,on='用户标签')
result['人数占比'] = result['人数占比'].apply(lambda x: '{:.2%}'.format(x))
result['金额占比'] = result['金额占比'].apply(lambda x: '{:.2%}'.format(x))
result = result.sort_values(by=['金额','人数'],ascending=[False,False])
result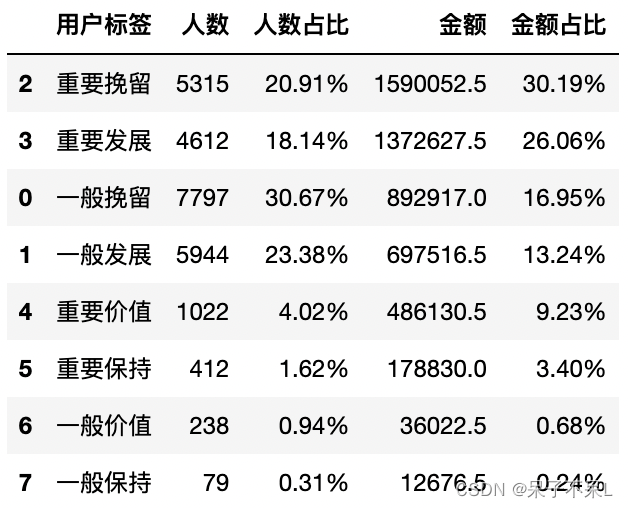
# !pip install pyecharts==1.9.1from pyecharts.charts import *
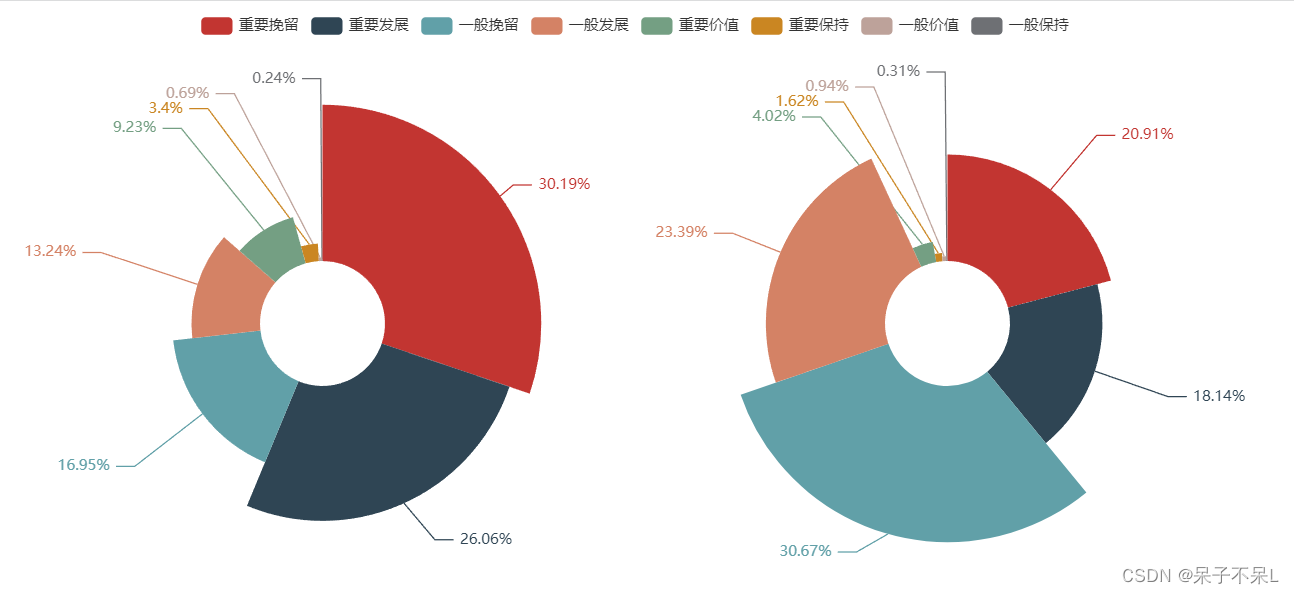
from pyecharts import options as opts# 绘制饼图
pie = Pie(init_opts=opts.InitOpts(width='1000px',height='500px')) # 实例化类,并调节大小
pie.add('交易金额',result[['用户标签','金额']].values.tolist(),radius=['20%','70%'],rosetype='radius',center=['25%','50%'] # 第一项是相对于画布的宽度,第二项是相对于画布的高度,默认是百分比形式,参考点为圆心
)
pie.add('交易人数',result[['用户标签','人数']].values.tolist(),radius=['20%','70%'],rosetype='radius',center=['75%','50%'] # 第一项是相对于画布的宽度,第二项是相对于画布的高度,默认是百分比形式,参考点为圆心
)
pie.set_series_opts(label_opts=opts.LabelOpts(formatter='{d}%')) # {a} 交易金额或人数;{b} 用户标签;{c} 指标的数值;{d} 百分比
pie.render('RFM模型分析.html')
pie.render_notebook()