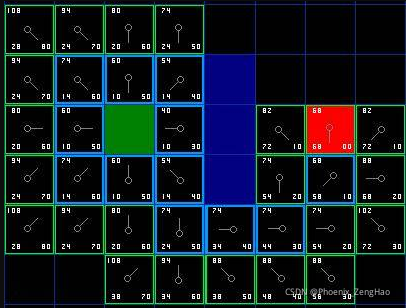
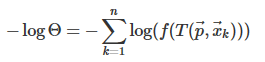前言

A*算法最初发表于1968年，由Stanford研究院的Peter Hart, Nils Nilsson以及Bertram Raphael发表。它可以被认为是Dijkstra算法的扩展。

由于借助启发函数的引导，A*算法通常拥有更好的性能。

一、

A*吸取了Dijkstra 算法中的cost_so_far，为每个边长设置权值，不停的计算每个顶点到起始顶点的距离（G），以获得最短路线，
同时也汲取贪婪最佳优先搜索算法中不断向目标前进优势，并持续计算每个顶点到目标顶点的距离（Heuristic distance），以引导搜索队列不断想目标逼近，从而搜索更少的顶点，保持寻路的高效。

二、原理与实现

1.启发函数

启发函数会影响A*算法的行为。

在极端情况下，当启发函数h(n)始终为0，则将由g(n)决定节点的优先级，此时算法就退化成了Dijkstra算法。
如果h(n)始终小于等于节点n到终点的代价，则A*算法保证一定能够找到最短路径。但是当h(n)的值越小，算法将遍历越多的节点，也就导致算法越慢。
如果h(n)完全等于节点n到终点的代价，则A*算法将找到最佳路径，并且速度很快。可惜的是，并非所有场景下都能做到这一点。因为在没有达到终点之前，我们很难确切算出距离终点还有多远。
如果h(n)的值比节点n到终点的代价要大，则A*算法不能保证找到最短路径，不过此时会很快。
在另外一个极端情况下，如果h()n相较于g(n)大很多，则此时只有h(n)产生效果，这也就变成了最佳优先搜索。

由上面这些信息我们可以知道，通过调节启发函数我们可以控制算法的速度和精确度。因为在一些情况，我们可能未必需要最短路径，而是希望能够尽快找到一个路径即可。这也是A*算法比较灵活的地方。

对于网格形式的图，有以下这些启发函数可以使用：

如果图形中只允许朝上下左右四个方向移动，则可以使用曼哈顿距离（Manhattan distance）。
如果图形中允许朝八个方向移动，则可以使用对角距离。
如果图形中允许朝任何方向移动，则可以使用欧几里得距离（Euclidean distance）。

2.伪代码

把起始格添加到 "开启列表" 
do 
{ 寻找开启列表中F值最低的格子, 我们称它为当前格. 把它切换到关闭列表. 对当前格相邻的8格中的每一个 if (它不可通过 || 已经在 "关闭列表" 中) { 什么也不做. } if (它不在开启列表中) { 把它添加进 "开启列表", 把当前格作为这一格的父节点, 计算这一格的 FGH }if (它已经在开启列表中) { if (用 G 值为参考检查新的路径是否更好, 更低的G值意味着更好的路径) { 把这一格的父节点改成当前格, 并且重新计算这一格的 GF 值. } }
} while( 目标格已经在 "开启列表", 这时候路径被找到) 
如果开启列表已经空了, 说明路径不存在.最后从目标格开始, 沿着每一格的父节点移动直到回到起始格, 这就是路径.

3.代码

主循化

void Astar(const int x, const int y)
{if(x == y){plan_path.clear();plan_path.push_back(x);isfindpath = true;std::cout << "---------------------------------------------------" << std::endl;std::cout << "* find! *" << std::endl;return;}openlist.clear();closelist.clear();//放入起点openlist.push_back(x);plan_ways_map[x]->G = 0;plan_ways_map[x]->H = Calculateh(y, x);plan_ways_map[x]->F = Calculatef(x);while (!openlist.empty()){int minidnode = Findleastf(openlist);//找到F值最小的点openlist.remove(minidnode);//从开启列表中删除closelist.push_back(minidnode);//放到关闭列表//1,找到下一步待选点std::vector<int> candiates = Getnextnode(minidnode);for(int i = 0; i < candiates.size(); ++i){//2,对某一点，如果它不在开启列表中，加入到开启列表，设置当前格为其父节点，计算F G Hif(!Isinlist(candiates[i], openlist)){plan_ways_map[candiates[i]]->parent = minidnode;plan_ways_map[candiates[i]]->G = Calculateg(x, candiates[i]);plan_ways_map[candiates[i]]->H = Calculateh(y, candiates[i]);plan_ways_map[candiates[i]]->F = Calculatef(candiates[i]);openlist.push_back(candiates[i]);}else{//3，对某一点，它在开启列表中，计算G值, 如果比原来的大, 就什么都不做, 否则设置它的父节点为当前点,并更新G和Fdouble tempg = Calculateg(x, candiates[i]);if(tempg > plan_ways_map[candiates[i]]->G){continue;}else{plan_ways_map[candiates[i]]->parent = minidnode;plan_ways_map[candiates[i]]->G = tempg;plan_ways_map[candiates[i]]->F = Calculatef(candiates[i]);}}//如果结束点出现在openlist则搜索成功if(Isinlist(y, openlist)){plan_ways_map[y]->parent = minidnode;std::cout << "---------------------------------------------------" << std::endl;std::cout << "* find! *" << std::endl;int i = y;while(i != -1){plan_path.push_back(i);i = plan_ways_map[i]->parent;}std::reverse(plan_path.begin(), plan_path.end());isfindpath = true;return;}}}std::cout << "---------------------------------------------------" << std::endl;std::cout << "* not find! *" << std::endl;return;
}

其他函数

//计算起点到当前点的代价
double Calculateg(const int x, const int idg) const 
{}//估计当前点到终点的代价
double Calculateh(const int y, const int idh) const 
{}//计算总代价，预置A*接口，Dijkstra相当于简化版A*
double Calculatef(const int idf) const 
{}//从list中找出总代价的点
int Findleastf(const std::list<int> &listx) const 
{}//从当前索引idx找到可行的下一点集合
std::vector<int> Getnextnode(const int idx) const 
{}//判断x点是否在list中
bool Isinlist(const int x, const std::list<int> &listx) const 
{}

三、可优化空间

1、选择排序更快的二叉树来作为开放列表，帮助我们更快地从开放列表中取出F值最小的点；
2、对何种情况下可以走斜线路径加以判断；
3、采用布兰森汉姆算法预先判断两点是否可以直接通行，可通行就直接返回两点的直线路径，不可直接通行再采用A星算法寻路，提高寻路效率；
4、A星算法得出寻路路径后，可采用弗洛伊德算法对路径进行平滑处理，使人物走动更为自然
5、设计两个或者更多寻路系统以便使用在不同场合，取决于路径的长度。这也正是专业人士的做法，用大的区域计算长的路径，然后在接近目标的时候切换到使用小格子/区域的精细寻路。
6. 从起点和终点同时开始找，双向A*