深度优先搜索广度优先搜索

article/2025/9/13 1:37:35

1 概述

算法是作用于具体的数据结构之上的，深度优先搜索算法和广度优先搜索算法都是基于图这种数据结构的。主要原因是因为图的这种数据结构表达能力很强，大部分涉及搜索的场景都可以抽象成图。
图上的搜索算法，最直接的理解就是，在图中找出从一个顶点出发，到另一个顶点的路径。具体方法有很多，比如今天要讲的两种最简单、最“暴力”的深度优先、广度优先搜索，还有 A*、IDA* 等启发式搜索算法。

2 广度优先搜索（Breath First Search）

广度优先搜索（Breath First Search）简称BFS，它是一种地毯式层层推进的搜索策略，即优先查找距离顶底近的，然后是次近的，依次往外搜索。如下图所示BFS搜索策略，搜索结果 1->2-3->4->5->6->7。

图2-1

算法描述：
1.从图中顶点V出发，首先访问V
2.依次访问V的，各个未被访问的邻接节点
3.依次从上述邻接节点出发，依次访问他们的各个未被访问的邻接节点。
4.如果此时图中任然有未被访问的顶点，则选择图中的一个未被访问的顶点作为起始顶点。重复广度优先搜索的过程，直到图中的所有节点均被访问过。

伪代码描述：

Vertex BFS(G,root){//初始化队列Q=Queue();    //root 顶点入队列Enqueue(root,Q);// label root as exploredvisited[root]=true;while(!Q.isEmpty()) {v=Dequeue(Q);if v is the goal thenreturn v;for all edges from v to w in G.adjacentEdges(v) doif !visited[w] thenvisited[w]=true;Q.enqueue(w);}return null;}

3 深度优先搜索（Depth First Search）

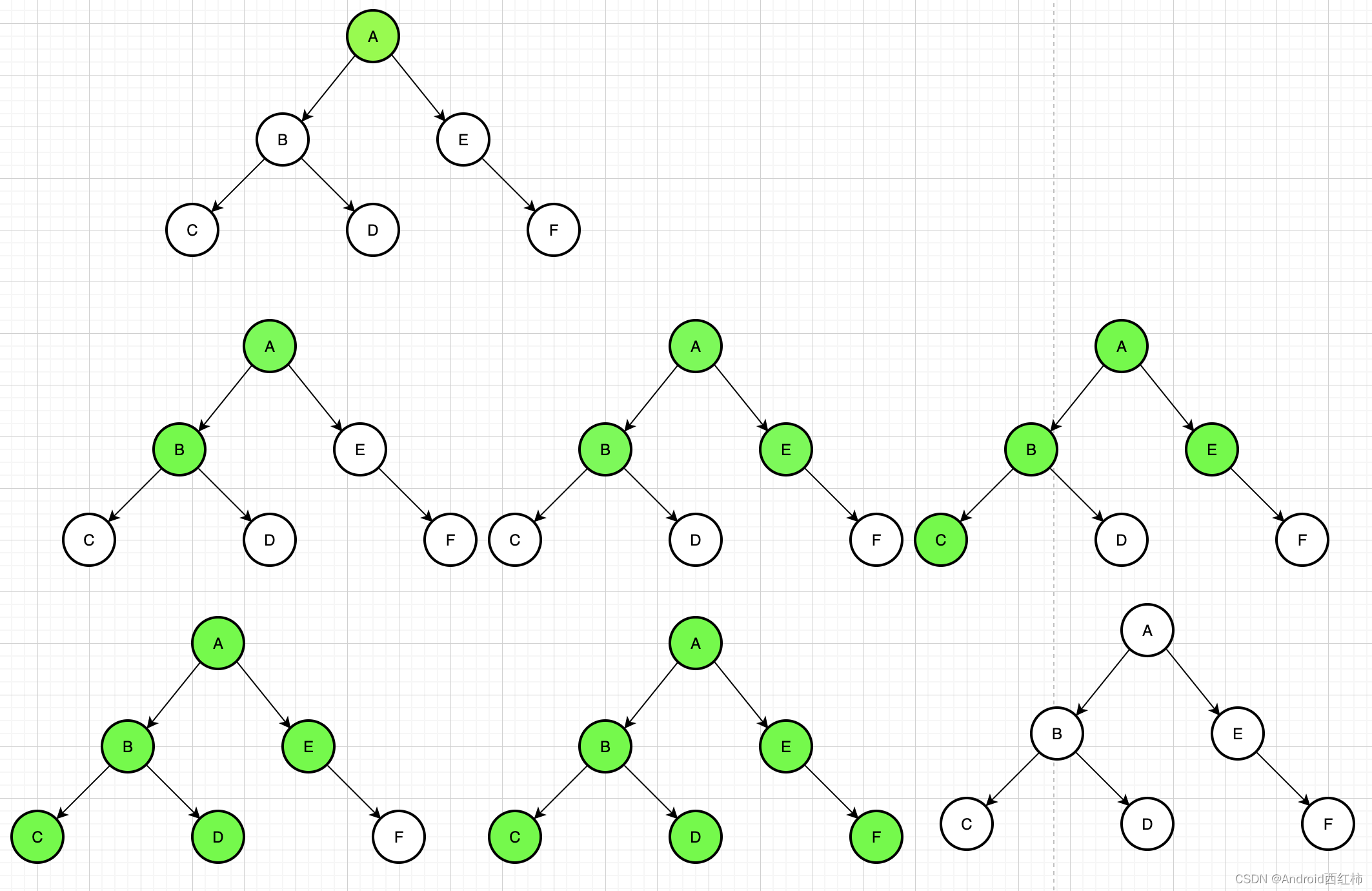
深度优先搜索（Depth First Search）简称DFS，其过程简要来说就是对每一个可能的分支路径深入到不能深入为止，而且每个节点只能访问一次。图2-1所示DFS搜索策略，搜索结果 1->2->5->7->3->6->4。

算法描述：
1.从图中某个顶点V出发，访问顶点V
2.依次从V未被访问的邻接点出发，对图进行深度优先遍历；直至图中和V有路径相通的顶点都被访问
3.若此时图中尚有顶点未被访问，则从一个未被访问的顶点出发，重新进行深度优先遍历，直到图中所有顶点均被访问过为止。

伪代码描述

DFS(G, v) //label v as discoveredvisited[v]=true;for all directed edges from v to w that are in G.adjacentEdges(v) doif  !visited[w] thenrecursively call DFS(G, w)

java 代码实现

import java.util.Iterator;
import java.util.LinkedList;
import java.util.Queue;
import java.util.Stack;/*** @author hsc* @date 2022/8/14 11:04 上午*/
public class Graph {//顶点的个数private int v;//邻接表private LinkedList<Integer> adj[];public Graph(int v) {this.v = v;adj = new LinkedList[v];for (int i = 0; i < v; i++) {adj[i] = new LinkedList<>();}}void addEdge(int v, int w) {adj[v].add(w);}void bfs(int s, boolean[] visited) {Queue<Integer> queue = new LinkedList<>();visited[s] = true;queue.add(s);while (!queue.isEmpty()) {Integer vertex = queue.poll();System.out.println(vertex);Iterator<Integer> i = adj[vertex].listIterator();while (i.hasNext()) {int n = i.next();if (!visited[n]) {visited[n] = true;queue.add(n);}}}}void bfs() {boolean[] visited = new boolean[v];for (int i = 0; i < v; i++) {if (!visited[i]) {bfs(i, visited);}}}void dfsUseRecurse(int s, boolean[] visited) {visited[s] = true;Iterator<Integer> i = adj[s].listIterator();System.out.println(s);while (i.hasNext()) {int n = i.next();if (!visited[n]) {dfsUseRecurse(n, visited);}}}void dfsUseStack(int s, boolean[] visited) {Stack<Integer> stack = new Stack<>();visited[s] = true;stack.add(s);while (!stack.isEmpty()) {Integer vertex = stack.pop();System.out.println(vertex);Iterator<Integer> i = adj[vertex].listIterator();while (i.hasNext()) {int n = i.next();if (!visited[n]) {visited[n] = true;stack.add(n);break;}}}}void dfs() {boolean[] visited = new boolean[v];for (int i = 0; i < v; i++) {if (!visited[i]) {dfsUseStack(i, visited);}}}public static void main(String[] args) {Graph graph = new Graph(7);graph.addEdge(0, 1);graph.addEdge(0, 2);graph.addEdge(0, 3);graph.addEdge(1, 4);graph.addEdge(4, 6);graph.addEdge(2, 5);graph.addEdge(5, 6);//从顶点0开始遍历graph.dfs();System.out.println("-----------------");graph.bfs();}
}

4 LeetCode实战

https://leetcode.cn/problems/number-of-islands/description/
思路：dfs 深度优先遍历，将已经访问节点置位0

    class Solution {private char[][] grid;private int row, col;public int numIslands(char[][] grid) {this.grid = grid;row = grid.length;col = grid[0].length;int ans = 0;for (int i = 0; i < row; i++)for (int j = 0; j < col; j++)if (grid[i][j] == '1') {dfs(i, j);ans++;}return ans;}void dfs(int i, int j) {if (i >= row || i < 0 || j < 0 || j >= col || grid[i][j] == '0') {return;}grid[i][j] = '0';dfs(i + 1, j);dfs(i - 1, j);dfs(i, j + 1);dfs(i, j - 1);}}

思路：使用bfs，将已经访问节点置位0

import java.util.LinkedList;
import java.util.Queue;/*** @author hsc* @date 2022/5/22 4:20 下午*/
class Solution {private char[][] grid;private int row, col;public int numIslands(char[][] grid) {this.grid = grid;row = grid.length;col = grid[0].length;int ans = 0;for (int i = 0; i < row; i++)for (int j = 0; j < col; j++)if (grid[i][j] == '1') {bfs(i, j);ans++;}return ans;}void bfs(int i, int j) {Queue<Integer> queue = new LinkedList<>();grid[i][j] = '0';queue.add(col * i + j);while (!queue.isEmpty()) {Integer id = queue.poll();int r = id / col;int c = id % col;if (r - 1 >= 0 && grid[r - 1][c] == '1') {queue.add((r - 1) * col + c);grid[r - 1][c] = '0';}if (r + 1 < row && grid[r + 1][c] == '1') {queue.add((r + 1) * col + c);grid[r + 1][c] = '0';}if (c - 1 >= 0 && grid[r][c - 1] == '1') {queue.add(r * col + c - 1);grid[r][c - 1] = '0';}if (c + 1 < col && grid[r][c + 1] == '1') {queue.add(r * col + c + 1);grid[r][c + 1] = '0';}}}}

参考文献：
[1]https://www.geeksforgeeks.org/breadth-first-search-or-bfs-for-a-graph/
[2] https://en.wikipedia.org/wiki/Breadth-first_search
[3]https://en.wikipedia.org/wiki/Depth-first_search