一，定义：

深度优先搜索的思路和树的先序遍历很像，下面是百度百科上的定义：

深度优先遍历图的方法是，从图中某顶点v出发：

（1）访问顶点v；

（2）依次从v的未被访问的邻接点出发，对图进深度优先遍历；直至图中和v有路径相通的顶点都被访问；

（3）若此时图中尚有顶点未被访问，则从一个未被访问的顶点出发，重新进行深度优先遍历，直到图中所有顶点均被访问过为止。　当然，当人们刚刚掌握深度优先搜索的时候常常用它来走迷宫.事实上我们还有别的方法，那就是广度优先搜索(BFS).

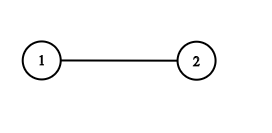
对于定义的理解，可以结合斐波那契数列（虽然用递归来写斐波那契是一种很糟糕的写法）来进行理解，如下图：

其中，右边这个树上的顺序是这样的：

可以结合遍历的思想来理解DFS；

DFS的题目大致可以分为两类：

1，对图的连通性进行检验：如迷宫问题，图的条件搜索。

2，DFS搜索顺序和规则问题，通过你穷举所有答案，找出符合条件的解。即爆搜问题。

看到这里，你可能会有些疑惑具体是怎样的问题，本文就针对DFS的原理进行，常见的题型进行了总结，附上代码和解题思路。

二，原理与分析

1，DFS连通性分析：

在测试连通性是，DFS的思路是与人们的思想是一致的，在一条路上，我是否可以在这条路上一直走下去，如果走不通，那我就返回原来的节点，换个方向，再沿着一条路走下去，直到成功。

针对连通性问题，我们还可以再进行分类：

1，无需回溯

在这种问题，只需要在每一步中，将搜索到的节点抛弃掉，对于当前搜索到的节点进行计数，最终统计所有能到达的点。

下面给出两个例题：
例1，红与黑(简单)

/** @Author: your name* @Date: 2022-02-11 13:39:15* @LastEditTime: 2022-02-11 13:56:51* @LastEditors: Please set LastEditors* @Description: 打开koroFileHeader查看配置 进行设置: https://github.com/OBKoro1/koro1FileHeader/wiki/%E9%85%8D%E7%BD%AE* @FilePath: \All code\26.cpp*/
#include<bits/stdc++.h>
using namespace std;
#define MAXN 100
char mp[MAXN][MAXN];
bool vis[MAXN][MAXN];
int W, H;
int ans;
int dx[4] = { 0, 1, 0, -1 };
int dy[4] = { 1, 0, -1, 0 };
void init()
{for (int i = 0; i < MAXN; i++){for (int j = 0; j < MAXN; j++){vis[i][j] = false;}}ans = 1;//由于在初始点位置，所以一开始就是一块黑砖
}
void dfs(int x, int y)//常用DFS套路
{for (int i = 0; i < 4; i++){int newx = x + dx[i];int newy = y + dy[i];if (newx >= 1 && newx <= H && newy >= 1 && newy <= W && mp[newx][newy] == '.' && vis[newx][newy] == false){ans++;vis[newx][newy] = true;dfs(newx, newy);}}
}
int beginx, beginy;
int main()
{while (1){cin >> W >> H;if (W == 0 && H == 0){break;}init();for (int i = 1; i <= H; i++)for (int j = 1; j <= W; j++){cin >> mp[i][j];if (mp[i][j] == '@'){beginx = i;beginy = j;}}dfs(beginx, beginy);cout << ans << endl;}return 0;
}

例2，Lake Counting(染色法简单）

/** @Author: your name* @Date: 2022-01-22 21:06:31* @LastEditTime: 2022-01-22 21:32:59* @LastEditors: Please set LastEditors* @Description: 打开koroFileHeader查看配置 进行设置: https://github.com/OBKoro1/koro1FileHeader/wiki/%E9%85%8D%E7%BD%AE* @FilePath: \All code\9.cpp*/
#include <bits/stdc++.h>
using namespace std;
#define MAXN 105
bool vis[MAXN][MAXN];
char mp[MAXN][MAXN];
int row,cow;
int dx[8] = {0, 0, -1, 1, -1, -1, 1, 1};
int dy[8] = {-1, 1, 0, 0, -1, 1, -1, 1};
void dfs(int x,int y)
{vis[x][y] = 1;for(int i =0;i<8;i++){int newx = x+dx[i];int newy = y+dy[i];if(newx>=0&&newy>=0&&newx<row&&newy<cow&&mp[newx][newy] == 'W'&&vis[newx][newy] ==0){dfs(newx,newy);}}
}int main()
{int i, j;int count =0;cin >> row >> cow;for (i = 0; i < row; i++)for (j = 0; j < cow; j++){cin >> mp[i][j];}for (i = 0; i < row; i++)for (j = 0; j < cow; j++){if(mp[i][j] == 'W'&&vis[i][j] == 0)//碰到一个后，就最这个区域进行DFS，并进行标记{dfs(i,j);count++;}}cout<<count;return 0;
}

有了这两个粒例子，相信大家开始对DFS有了一个大概的认识。

二，需要回溯：迷宫类问题

这一类问题就像我在刚刚导论里面提及的，如果这条路不同，则需要设置回溯，进行恢复现场。最经典的莫过于走迷宫问题（简单）：

/** @Author: your name* @Date: 2022-01-22 21:06:31* @LastEditTime: 2022-01-22 22:12:20* @LastEditors: Please set LastEditors* @Description: 打开koroFileHeader查看配置 进行设置: https://github.com/OBKoro1/koro1FileHeader/wiki/%E9%85%8D%E7%BD%AE* @FilePath: \All code\9.cpp*/
#include <bits/stdc++.h>
using namespace std;
#define MAXN 505
bool vis[MAXN][MAXN];
char mp[MAXN][MAXN];
int row, cow;
int dx[4] = {0, 0, -1, 1};
int dy[4] = {-1, 1, 0, 0};
bool flag = false;
void dfs(int x, int y)
{vis[x][y] = 1;for (int i = 0; i < 4; i++){int newx = x + dx[i];int newy = y + dy[i];if (newx >= 0 && newy >= 0 && newx < row && newy < cow && vis[newx][newy] == 0){if (mp[newx][newy] == '.')dfs(newx, newy);if (mp[newx][newy] == 'E')flag = true;}}
}
void init()
{for (int i = 0; i < row; i++)for (int j = 0; j < cow; j++){vis[i][j] = 0;}
}
int main()
{int i, j;int count = 0;int row_s, cow_s;while (cin >> row >> cow){flag = false;for (i = 0; i < row; i++)for (j = 0; j < cow; j++){cin >> mp[i][j];if (mp[i][j] == 'S'){row_s = i;cow_s = j;}}init();dfs(row_s, cow_s);if (flag == true){cout << "Yes" << endl;}else{cout << "No" << endl;}}return 0;
}

除此之外，还有一个例题，用于计数的：马走日

这个题只是将迷宫问题的路径选择和成功条件进行了一个改变，也是简单的搜索问题：

/** @Author: your name* @Date: 2022-02-11 14:44:55* @LastEditTime: 2022-02-11 15:30:56* @LastEditors: Please set LastEditors* @Description: 打开koroFileHeader查看配置 进行设置: https://github.com/OBKoro1/koro1FileHeader/wiki/%E9%85%8D%E7%BD%AE* @FilePath: \All code\28.cpp*/
#include <iostream>
using namespace std;
#define MAXN 15
int mp[MAXN][MAXN];
bool vis[MAXN][MAXN];
int row, cow, newx, newy;
int ans;
int dx[8] = { -2, -2, 2, 2, -1, -1, 1, 1 };
int dy[8] = { 1, -1, 1, -1, -2, 2, -2, 2 };
void init()
{for (int i = 0; i < MAXN; i++){for (int j = 0; j < MAXN; j++){vis[i][j] = false;}}ans = 0;
}void dfs(int x, int y, int depth)
{for (int i = 0; i < 8; i++){int newx = x + dx[i];int newy = y + dy[i];if (newx >= 1 && newx <= row && newy >= 1 && newy <= cow && vis[newx][newy] == false){vis[newx][newy] = true;if (depth == row * cow - 1)//由于这里是newx，并不是已经递归到新一层中，所以这里需要减1{ans++;}dfs(newx, newy, depth + 1);vis[newx][newy] = false;}}
}int main()
{int T;cin >> T;while (T--){cin >> row >> cow >> newx >> newy;init();vis[newx + 1][newy + 1] = true;dfs(newx + 1, newy + 1, 1);//这里要注意，我在从第一步开始的时候，就已经算是处在第一层了，不是第0层。cout << ans << endl;}return 0;
}

我在开始这一道题的时候，就犯下了这样一个错误：将截止条件的层数看错。大家在写代码的时候要注意这个问题。

总结一下DFS的模板

function dfs(当前状态){
if(当前状态 == 目的状态){
···
}
for(···寻找新状态){
if(状态合法){
vis[访问该点]；
dfs(新状态);
?是否需要恢复现场->vis[恢复访问]
}
}
if(找不到新状态){
···
}
}

2，穷举解决问题

例：部分和问题：

#include <bits/stdc++.h>
using namespace std;
int n, k;
int a[35];bool dfs(int id, int sum)
{if (sum == k)return 1;if (id > n)return 0;if (1 == dfs(id + 1, sum + a[id]))return 1;if (1 == dfs(id + 1, sum))return 1;return 0;
}int main()
{cin >> n >> k;for (int i = 1; i <= n; i++){cin >> a[i];}if (1 == dfs(1, 0)){puts("YES");}else{puts("NO");}return 0;
}

也很简单，只要一次在每一步中讨论当前这个数是否选取，即可。对于这个问题，如果是想要找出所有相加为k的序列中，个数最少的一个，也可以利用穷举的方法来写。同时也可以利用动态规划的知识来解题。读者可以下去自己思考。