概述

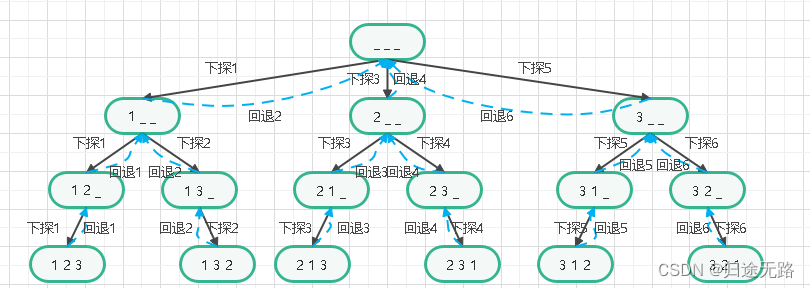
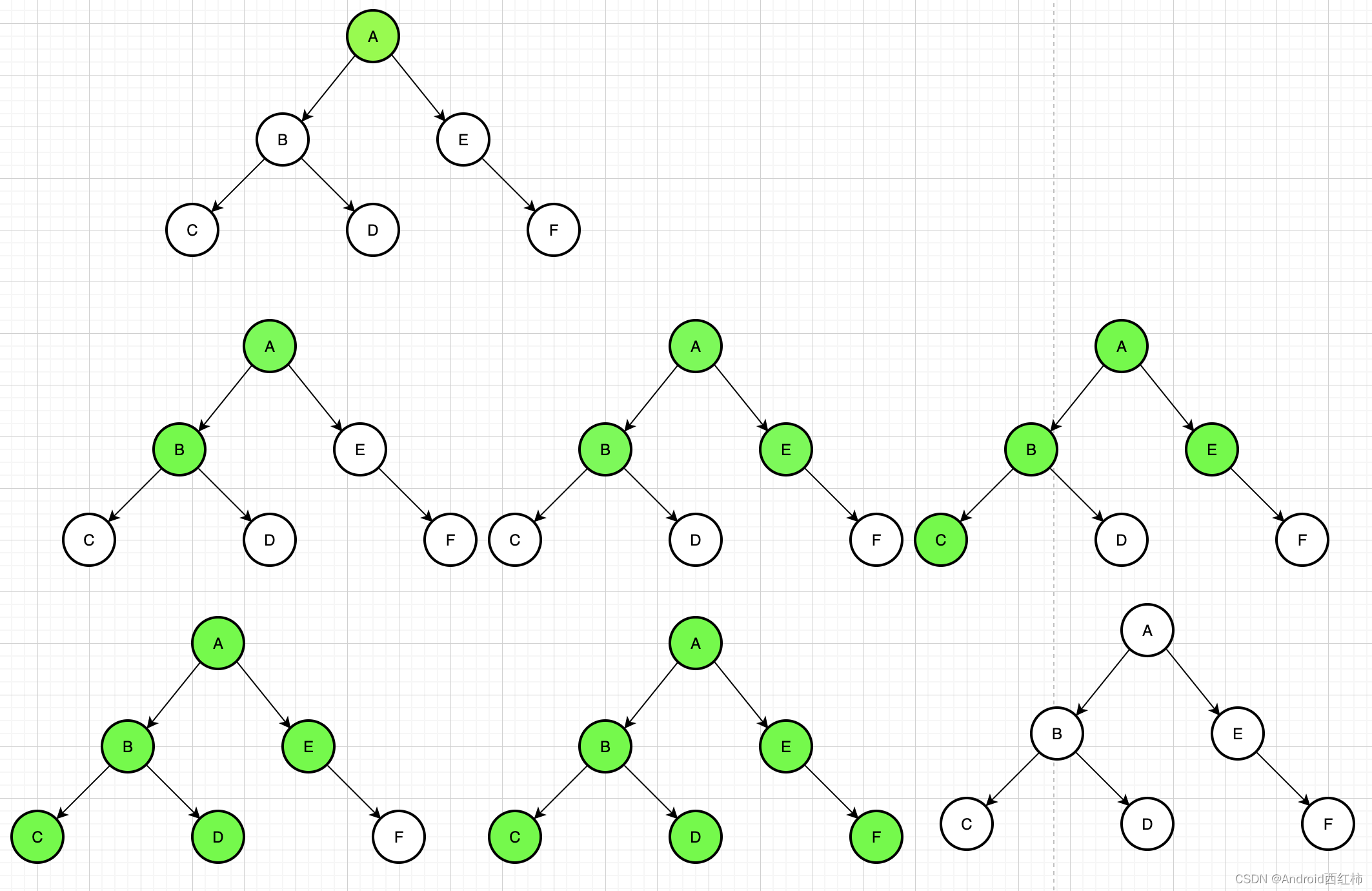
深度优先搜索（Depth First Search，DFS），是最常见的图搜索方法之一。深度优先搜索沿着一条路径一直走下去，无法行进时，回退回退到刚刚访问的结点，似不撞南墙不回头，不到黄河不死心。深度优先遍历是按照深度优先搜索的方式对图进行遍历。

tips:后被访问的顶点，其邻接点先被访问。所以这是后来的先访问,可以借助栈的特性实现,而递归就是用栈来实现的,因此可以使用递归

算法

1.初始化图中所有顶点未被访问.

2.从图中的某个顶点v出发，访问v并标记已访问.

3.依次检查v的所有邻接点w，如果w未被访问，则从w出发进行深度优先遍历（递归调用，重复2—3步)

细节描述

1.想要弄懂邻接矩阵的深度优先搜索,首先需要保证你的邻接矩阵已经非常熟悉了

2.关于怎么使用标记,这里可以创建一个数组,起名visited,得出visited[],其中的大小是你所存储的图中,顶点的个数,全部初始化为false,因为是bool型数组. 还有,你的顶点是存放在顶点集数组中,每个元素都有其对应的元素下标,而这些下标都是与visited数组的下标是一一对应的,当你输出顶点集的某个元素比如第3个元素,那么visited[2]就会被标记为true,代表你已经访问过该顶点了

3.递归的实现,简单来说就是函数套函数,看面的代码

当该节点是邻接点(代表G.Edge==1),并且未被访问对其进行深度优先遍历,怎么保证所有顶点都被访问到?是由下面的for语句进行保证的,可以自己体会一下.

void DFS_AM(AMGragh G, int v)
{cout << G.vex[v] << " ";visited[v] = true;for (int w = 0; w < G.vexnum; w++){if (G.Edge[v][w] && !visited[w]){DFS_AM(G, w);}}
}

4 .访问的邻接点的顺序是从小到大的,这是for循环决定的

完整代码

#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
#include<algorithm>
using namespace std;const int maxnum = 100;
bool visited[maxnum];
typedef char VexType;
typedef int EdgeType;struct AMGragh
{VexType vex[maxnum];EdgeType Edge[maxnum][maxnum];int vexnum, edgenum;
};int locatevex(AMGragh G, VexType x)
{for (int i = 0; i < G.vexnum; i++){if (x == G.vex[i]){return i;}}return -1;
}void CreatAMGragh(AMGragh& G)
{VexType u, v;cout << "请输入顶点数和边数" << endl;cin >> G.vexnum >> G.edgenum;cout << "请输入顶点信息" << endl;for (int i = 0; i < G.vexnum; i++){cin >> G.vex[i];}for (int i = 0; i < G.vexnum; i++){for (int j = 0; j < G.vexnum; j++){G.Edge[i][j] = 0;}}cout << "请输入每条边所依附的两个顶点" << endl;while (G.edgenum--){VexType u, v;cin >> u >> v;int i = locatevex(G, u);int j = locatevex(G, v);if (i != -1 && j != -1){G.Edge[i][j] = G.Edge[j][i] = 1;}else{cout << "输入有误,重新输入" << endl;G.edgenum--;}}
}void Print(AMGragh G)
{for (int i = 0; i < G.vexnum; i++){for (int j = 0; j < G.vexnum; j++){cout << G.Edge[i][j] << " ";}cout << endl;}
}void DFS_AM(AMGragh G, int v)
{cout << G.vex[v] << " ";visited[v] = true;for (int w = 0; w < G.vexnum; w++){if (G.Edge[v][w] && !visited[w]){DFS_AM(G, w);}}
}int main()
{AMGragh G;CreatAMGragh(G);Print(G);cout << "请输入图的起点" << endl;VexType c;cin >> c;int i = locatevex(G, c);if (i != -1){cout << "深度优先" << endl;DFS_AM(G, i);}else{cout << "输入有误" << endl;}system("pause");return EXIT_SUCCESS;
}