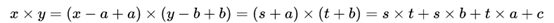本文首发公众号VenusBlockChain，关注公众号后可免费阅读！VenusBlockChain致力于区块链技术研究，传播区块链技术和解决方案、区块链应用落地、区块链行业动态等。有兴趣的小伙伴们，欢迎关注。

安全多方计算（Secure Multi-party Computa-tion，sMPC）是分布式密码学的理论基础，也是分布式计算研究的一个基本问题，最早由姚期智于1982年通过姚氏百万富翁问题提出。

简单的说，安全多方计算是指一组人，比如$P_1....P_n$ ，共同安全的计算函数$f(x_1,...,x_n)=(y_1,...,y_n)$。函数的n个输入分别由n个参与者秘密掌握，设$P_i$的秘密输入是$x_i$ ，并且在计算结束后，$P_i$ 得到输出$y_i$ 。这里的安全性是要求即使在某些参与者有欺骗行为的情况下保证计算结果的正确性，即计算结束后每个诚实的参与者$P_i$ 都能得到正确的输出$y_i$，同时还要求保证每个参与者输入的保密性，即每个参与者$P_i$ 除了$(x_i,y_i)$外，得不到任何其他信息。

安全多方计算的一般实现方法有四种：同态加密密码体制、不经意传输协议、线性密钥共享体制、混淆电路框架。
这一篇先介绍基于同态加密密码体制的安全多方计算协议。

1 同态门限密码体制

具有加法同态性的门限密码体制是构造安全多方计算协议的一个基本工具。具体来说，设$（sk,pk,M,C,E,D）$是一个公钥密码体制，其中$sk$是私钥，$pk$是公钥，$M$是明文空间，$C$是密文空间，$E$和$D$分别是加密算法和解密算法。特别是明文空间$M$和密文空间$C$都是带有某种运算的有限交换群。对任意的明文$m\in M$，加密得到密文$c=E(m)$，解密过程为$D(c)=D(E(m))=m$。

对于任意的$m_1,m_2\in M$，满足$E(m_1)\ast E(m_2)=E(m_1+m_2)$，我们就称该密码体制具有加法同态性，其中“+”表示明文空间的运算，“$\ast$”表示密文空间的运算。加法同态性质说明：可以由$m_1$和$m_2$的密文直接得到$m_1+m_2$的密文。

具有加法同态性的密码体制有很多，经常用到的是Paillier密码体制。门限密码体制是把解密的权力利用门限控制，比如$(t,n)$门限就是要求只有$n$个参与者中的至少$t$个人联合才能解密得到明文，而任何少于$t$个人都无法得到明文。Desmedt和Frankel在其文献“Threshold Cryptosystem(1990)”中指出，任何一个公钥密码体制理论上都可以门限化。

门限密码体制基本的思路是公布公钥$pk$，但是将私钥$sk$在$n$个人中按照Shamir$(t,n)$门限体制进行共享。设$P_i$得到子密钥$s{k}_i$，$1\le i\le n$。解密的时候，设要联合解密密文$m\in M$，$P_i$将自己的子密钥作用在密文上得到$m_i=D_{s{k}_i}(c)$，$1\le i\le t$。最后由$m_1,...,m_t$就可以得到明文$m$。

注意：解密的时候并不是将私钥$sk$重构出来，否则私钥一旦被某个参与者知道，该门限密码体制就变得不安全了。

2 基于Paillier加法同态密码体制的安全多方计算协议

设 P = { P 1 , . . . , P n } P=\{P_1,...,P_n\} P={P1​,...,Pn​}是参与者集合，他们要共同计算函数$f(x_1,...,x_n)$，其中$P_i$掌握输入$x_i$，$1\le i\le n$。讨论密码学模型下的安全多方计算，攻击者结构是$\Theta$。设$（sk,pk,M,C,E,D）$是一个基于Paillier加法同态性的门限密码体制，并且$P_1,...,P_n$已经掌握了相关参数（即各自的公钥、私钥等）。这里用到的门限密钥共享体制满足对于任意的$m_1,m_2\in M$，任意的被收买集合$\theta \in \Theta$都无法区分$E(m_1)$和$E(m_2)$。

下面的安全多方计算协议分为输入阶段、计算阶段和输出阶段。

(1)输入阶段

每个参与者$P_i$，$1\le i\le n$，将自己的输入$x_i$用公钥$p{k}_i$进行加密得到密文$E(x_i)$，然后把密文$E(x_i)$公开。

(2)计算阶段

假设要计算的函数$f$已经表示成某个有限域上$K$的多项式，这里取$K=Z_p$，$p$是$N$的素因子。因此，在计算阶段的每一步依然是处理一个$x+y$或$xy$，其中$x,y\in K$。并采用加密体制进行隐藏，即每个参与者得到的只是输入和输出的密文。由于经过输入阶段，可以假设每个参与者已经得到输入的密文$E(x)$和$E(y)$，于是计算阶段的每一步就是使所有参与者最后得到$E(x+y)$或$E(xy)$，然后作为下一步计算的输入计算。

计算$“x+y”$：由于采用的密码体制具有加法同态性质，那么每个参与者由$E(x)$和$E(y)$，不需要交互只进行直接计算$E(x)\ast E(y)$就可以得到$E(x+y)$。

计算$“xy”$：每个参与者$P_i$，$1\le i\le n$，秘密选取随机数$d_i\in M$，将用公钥$pk$加密，公开$E(d_i)$。根据加法同态性，将所有参与者都得到$c^{\prime }=E(d_1+...+d_n+x)=E(d_1)\ast ...\ast E(d_n)\ast E(x)$，然后联合对$c^{\prime }$进行解密，得到$d=D(c^{\prime })=d_1+...+d_n+x$。参与者$P_1$计算$z_1=d-d_1$，$P_i$计算$a_i=-d_i$，$2\le i\le n$，显然有$x={\sum }_{i=1}^n{a}_i$。根据加密体制的加法同态性，每个参与者$P_i$，$1\le i\le n$，计算得到$E((a_{i}y)$并将结果公开。例如，如果密文空间对应的运算时乘法，那么$E((a_{i}y)=(E((y){)}^{a_i}$。最后，所有参与者计算$E((a_{1}y)\ast ...\ast E((a_{n}y)=E({\sum }_{i=1}^n{a}_{i}y)=E(xy)$。

(3)输出阶段

由于到计算阶段的最后，所有参与者都已经得到最后函数值的密文$E(f(x_1,...,x_n))$，因此输出阶段就是所有参与者联合对$E(f(x_1,...,x_n))$进行解密得到最后的函数值。

3 往期回顾

数字签名系列

• 图解 ECDSA 签名与验签基本原理
• 图解 BLS 签名与验签基本原理
• BLS 签名理论原理和工程实现
• 基于 RSA 的实用门限签名算法
• 门限密钥共享技术原理
• 隐私保护利器之环签名实现原理
• 多重签名 MultiSig：Schnorr 协议与 ECDSA 协议
• 一种高效的数字签名算法ED25519
• Schnorr 协议：零知识身份证明和数字签名

智能合约隐私计算

• 智能合约隐私计算：开篇
• 智能合约隐私计算：同态加密应用举例
• 智能合约隐私计算：再谈Paillier同态加密算法
• 智能合约隐私计算：基于FO承诺的零知识证明
• 智能合约隐私计算：基于FO承诺的零知识承诺相等性证明和平衡验证

密码学承诺系列

• Pedersen commitment

同态加密系列

• 智能合约隐私保护技术之同态加密
• 智能合约隐私计算之再谈Paillier同态加密算法

4 参考资源

[1] 密钥共享体制和安全多方计算[M]，刘木兰、张志芳著。