当特征选择完成后,可以直接训练模型了,但是可能由于特征矩阵过大,导致计算量大,训练时间长的问题,因此降低维度也是必不可少的。
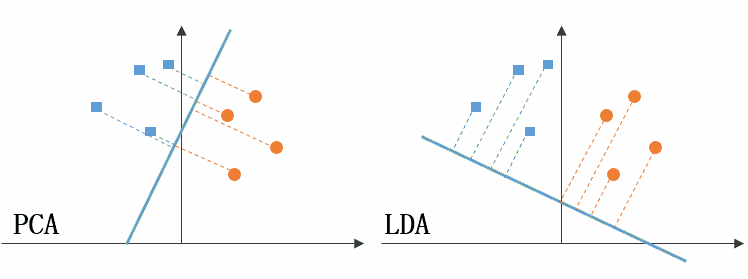
常见的降维方法除了以上提到的基于 L1 惩罚项的模型以外,另外还有主成分分析法(PCA)和线性判别分析(LDA),线性判别分析本身也是一个分类模型。PCA和LDA有很多相似点,其本质时要将原始的样本映射到维度更低的样本空间中,但是PCA和LDA的映射目标不一样:PCA是为了让映射后的样本具有最大的发散性;而LDA是为了让映射后的样本有最好的分类性能。所以说PCA是一种无监督的降维方法,而LDA是一种有监督的降维方法。
高维度数据在任何模型中都可能表现很差。你肯定听过一个词——过拟合。回忆一下过拟合的表象:模型在训练集中表现优秀,但是在测试集中表现很差,原因是,你的模型太复杂了,复杂到把训练集中的数据噪声都学习进去了。那么模型的复杂度是跟数据的维度正相关的(对于大多数模型来说,数据维度就是正比于模型复杂度的)。
如果想要更深入的理解,建议查一下 维度诅咒 这个词。会有文章详细解释这个现象究竟为什么会产生。归根结底是随着数据维度的增长,样本与样本之间的距离变远了,所有的数据都位于空间的边缘,想要训练出来理想的模型,就必须要以指数级增加训练样本个数。
随着维度的上升,基于距离的方法开始失效。因为维度很高后,distance的分布的密度越来越高,且越来越聚集在中心处,即任何高维空间里的两点之间的距离几乎没有差别。
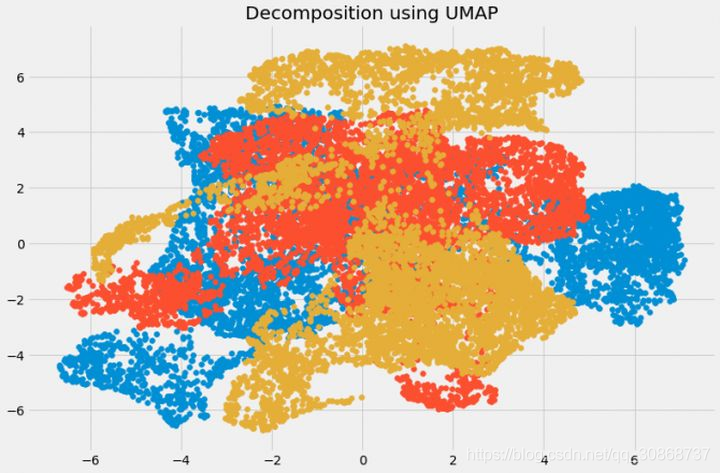
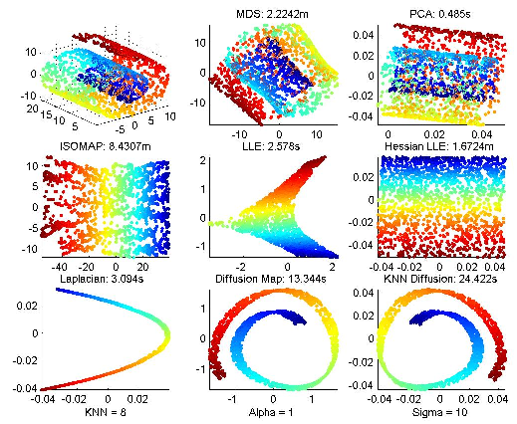
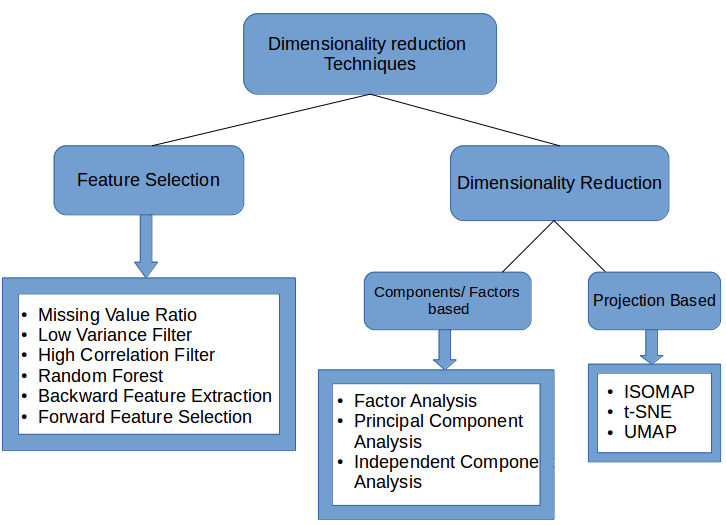
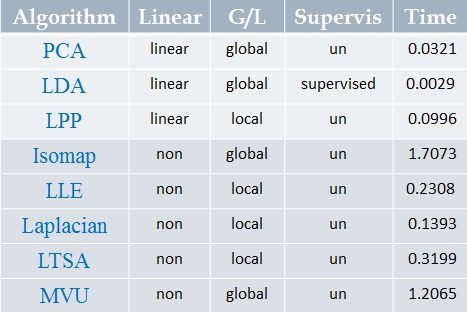
处理高维数据最常用的方法就是降维,降维后再使用聚类算法可能会更有效,很多降维算法都是很常用的,常用的机器学习框架都能够直接调用,下图给出了常用的降维算法:

线性方法
一、PCA
1. 基本思想:
主成分分析(Principal components analysis,以下简称PCA)是最重要的降维方法之一。在数据压缩消除冗余和数据噪音消除等领域都有广泛的应用。
PCA顾名思义,就是找出数据里最主要的方面,用数据里最主要的方面来代替原始数据。
第一种解释是样本点到这个直线的距离足够近,第二种解释是样本点在这个直线上的投影能尽可能的分开。
我们知道“基于最小投影距离”就是样本点到这个超平面的距离足够近,也就是尽可能保留原数据的信息;而“基于最大投影方差”就是让样本点在这个超平面上的投影能尽可能的分开,也就是尽可能保留原数据之间的差异性。
假如我们把n’从1维推广到任意维,则我们的希望降维的标准为:样本点到这个超平面的距离足够近,或者说样本点在这个超平面上的投影能尽可能的分开。
基于上面的两种标准,我们可以得到PCA的两种等价推导。
2. 优缺点
作为一个非监督学习的降维方法,它只需要特征值分解,就可以对数据进行压缩,去噪。因此在实际场景应用很广泛。
PCA算法的主要优点有:
1)仅仅需要以方差衡量信息量,不受数据集以外的因素影响。
2)各主成分之间正交,可消除原始数据成分间的相互影响的因素。
3)计算方法简单,主要运算是特征值分解,易于实现。
4)当数据受到噪声影响时,最小的特征值所对应的特征向量往往与噪声有关,舍弃能在一定程度上起到降噪的效果。
PCA算法的主要缺点有:
1)主成分各个特征维度的含义具有一定的模糊性,不如原始样本特征的解释性强。
2)方差小的非主成分也可能含有对样本差异的重要信息,因降维丢弃可能对后续数据处理有影响。
为啥W’XX’W可以度量样本的差异性。最后得出结论:XX’就是X的协方差矩阵,其中对角线元素为各个字段的方差,而非对角线元素表示变量i和变量j两个字段的协方差。
注意:
由于 PCA 减小了特征维度,因而也有可能带来过拟合的问题。PCA 不是必须的,在机器学习中,一定谨记不要提前优化,只有当算法运行效率不尽如如人意时,再考虑使用 PCA 或者其他特征降维手段来提升训练速度。
降低特征维度不只能加速模型的训练速度,还能帮我们在低维空间分析数据,例如,一个在三维空间完成的聚类问题,我们可以通过 PCA 将特征降低到二维平面进行可视化分析。
二、LDA
基本思想:LDA是一种监督学习的降维技术,也就是说它的数据集的每个样本是有类别输出的。这点和PCA不同。PCA是不考虑样本类别输出的无监督降维技术。 我们要将数据在低维度上进行投影,投影后希望每一种类别数据的投影点尽可能的接近,而不同类别的数据的类别中心之间的距离尽可能的大。
二者对比
LDA用于降维,和PCA有很多相同,也有很多不同的地方,因此值得好好的比较一下两者的降维异同点。
首先我们看看相同点:
1)两者均可以对数据进行降维。
2)两者在降维时均使用了矩阵特征分解的思想。
3)两者都假设数据符合高斯分布。
我们接着看看不同点:
1)LDA是有监督的降维方法,而PCA是无监督的降维方法。
2)LDA降维最多降到类别数k-1的维数,而PCA没有这个限制。
3)LDA除了可以用于降维,还可以用于分类。
4)LDA选择分类性能最好的投影方向,而PCA选择样本点投影具有最大方差的方向。
非线性方法
参考链接
[1] 线性代数:如何求特征值和特征向量? 2017.12
[2] LDA和PCA降维 2020.3