数据结构之——栈

一：栈的定义：

栈是限定仅在表尾进行插入和删除操作的线性表，栈又称为先进后出（Last In First Out）的线性表，简称LIFO结构。（栈就像一个杯子，我们只能在杯口（栈顶）向这个杯子里倒入水（进栈）或使其倒出水（出栈），而不能在杯底（栈底）进行这些操作，而且我们喝水的时候不能直接喝底下的水，只能先喝上面的水（出栈），才能去喝下面的水）

栈顶：允许插入和删除的一端称为栈顶。
栈底：不可以进行插入和删除操作。
空栈：不含任何数据元素的栈称为空栈。

	理解栈的定义需要注意几点：
1：它是一个线性表，即说明栈元素具有  线性关系，即  前驱后继  关系。只不过它是一种特殊的线性表而已。
2：定义中说在线性表的表的表尾进行插入和删除操作，注意这里表尾指的是栈顶 ，不是栈底。
3：栈的特殊之处就在于其限制了这个线性表的插入和删除始终在栈顶进行。这使得栈底是固定的，最先进栈的只能在栈底。
4： 栈的插入操作：叫进栈，也叫压栈、入栈。栈的删除操作：叫出栈，也叫弹栈。

二：栈的抽象数据类型：

	ADT 栈（stack）Date  和线性表相同。元素有相同的数据类型，相邻元素有前驱和后继的关系OperationInitStack (*S): 初始化操作，建立一个空栈S。DestoryStack（*S）:如果栈存在则销毁它。ClearStack (*S) : 将栈清空。StackEmpty（*S）:如果栈为空则返回true,否则返回false。GetTop（*S，*e）:如果栈存在且非空，用e返回S的栈顶储存的值。Push (*S, e) :若栈S存在，插入新的元素e到栈S中并成为栈顶元素。 Pop (*S，*e) :删除S中栈顶元素，并用e返回其值。StackLength (S) :返回栈S的元素个数。endADT

三：栈的顺序存储结构及其实现：

1: 预说明：

	1：在栈中我们我们把空栈的top值设为 -12：把满栈的top值设为 maxsize - 13：把下标为0的一端作为栈底‘1、2’的解释：top 值的位置都是其数组所对应的下标位置，数组的下标范围是0 ~ n - 1，且每个top所在的位置都是已经存储了数据的，每次我们新存储数据之前都要先要top++来运动到下一个结点，所以top 的最大值为maxsize - 1, 空栈时的top 值为 -1 ，因为移动了maxsize次后top = maxsizeof - 1‘3’ 的解释：因为我们的首元素都存在栈底（因为它们是最先进栈的），变化最小。

2：栈的顺序存储结构——结构定义：

#define maxsize 在此处输入自定义的一个数
typedef int ElemType		//ElemType 的类型根据实际情况而定 typedef struct {ElemType date[maxsize]; //这个maxsize 通过我们事先的预定义来改变改栈的长度大小 int top;  				//这个  top  用于栈顶的指针，即目前栈顶所在数组中的位置}SqStack;

3:栈的顺序存储结构——进栈操作

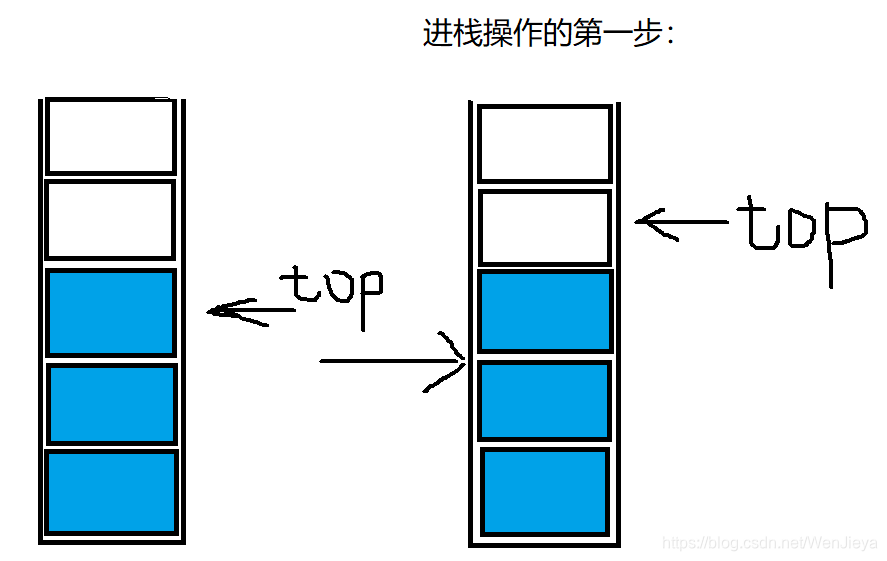
// 进行一次进栈操作
int sqstack_insert(sqstack *p, ElemType e) {//这个指针 P 接收的是包含我们要进行操作的那个栈的结构体的地址//这个 e 接受的是我们想向这个栈中放入的数据if (p->top >= maxsize - 1) {printf("当前您的栈已满，不可进行此操作");system("pause");	/*该行代码是程序的停顿操作，按任意键可继续向下执行*/return ERROR;  /* 程序进行到这一步说明我们的栈已经满了，不可再进行进栈操作，返回 Error*/}else {p->top++;/* 这行很重要：这里是把我们的栈顶向上移动以为，因为当前所在的栈顶是已经存有数据的*/p->data[p->top] = e;/*  注意上面这行代码，我们括号中要写p->top，而不是top,因为我们的top是包含在这个结构体当中的 */}return OK; /*如果我们的程序进行到了这一步，说明我们的进栈操作已经结束了，返回 OK*/
}

4: 栈的顺序存储结构——出栈操作

// 进行一次出栈操作
int sqstack_del(sqstack *p, ElemType *e) {
// 函数前用ElemType 是因为我们这个函数要返回一个ElemType型的数值
// 这个 e 是用来返回我们退出的那个栈中存储的数据if (p->top == -1) {printf("当前您的栈为空栈，不可以进行此操作.");/*若top的值为-1，则代表这个栈为空栈，不能进行出栈操作，返回ERROR */system("pause");return ERROR;}else {*e = p->data[p->top];//注意这里是 *e 而不是 e ,因为我们这里是要传递值而不是地址p->top--;/* 因为我们进行了一次退栈操作，所以把栈顶指针向下移动一位，移到下一个结点 */}return OK;// 因为这里是返回值而不是地址，所以用 *e
}

5: 栈的顺序存储结构——两栈共享空间

	两栈共享空间其实就是两个栈共享同一个数组的空间，前面我们说的都是一个
数组一个栈，但是这个是一个数组两个栈， 但是：“每个栈各有一个栈顶和一个栈
底，怎么分呢？” ， 我们规定：“让一个栈的栈顶为数组的始端，即下标为0处，让
另一个栈的栈底为数组的末端，即下标为maxsize - 1处。”，通过这个方法，如果
两个栈增加元素，就是从两个端点向中间延伸。

预说明：

	前面已经说过了如果一个栈把数组的下标为0的一端作为栈底的话，其空栈时
top的值应该为-1，同理，如果一个栈把数组的下标为maxsize - 1的一端作为栈
底的话，其空栈时top的值应该为maxsize。

但是我们怎么知道数组有没有满呢？（看下面图3）

所以，通过图3我们可以知道：当两个栈均满时top1和top2见面，且top1 + 1 = top2

两栈共享空间的进栈和出栈：

 	上面我们已经给出了普通的栈的输入和输出的代码，其实两栈共享空间的这个进栈和出栈的代码差不多，只不过有一点不同：普通的栈：我们判断是否栈满时的代码是： if(top == maxsize - 1)两栈共享：我们判断是否栈满时的代码是： if(top1 + 1 == top)//上面已经说过了为什么是这样

四：栈的链式存储结构及其实现：

1：预说明：

	联想一下线性表的链式存储结构，其每个结点的指针域中都存放着下一个结点的
地址，通过这种方式来将这些结点直接联系起来，栈也是一个线性表，也具有线性关
系，同理，栈的链式存储结构中每个结点的也有个指针域，并且也保存着下一个结点
的地址，还有一个很重要的：线性表的链式存储结构中会有一个头指针，其指向链表
的头结点或者首元结点，在栈的链式存储结构中也有一个这个，但是栈中好像有个东
西的作用和它差不多，所以，在栈中，我们把top和头指针合二为一了(即把栈顶放在
了这个单链表的头部)。并且，已经有了栈顶在头部了，单链表中比较常用的头结点
也失去了意义，通常对于链栈来说，是不要头结点的。（因为我们进栈的操作很像
链表中的头插法，而且我们栈顶就是来进行进栈和出栈的工作的，所以我们对它进
行操作就可以，不需要再弄一个头结点出来，这样反而还会增加我们的工作量）

2：栈的链式存储结构——结构定义

typedef struct StackNode {ElemType data;	//每个结点储存数据处StackNode *next;/* 这个定义值的是：next是指向Struct StackNode型的指针变量，即指向包含某个结点的结构体 */
}StackNode, *LinkStackPtr;
/* 通过这个预定义，则这两串代码等同：StackNode *next = LinkStackPtr next
*/
typedef struct LinkStack{LinkStackPtr top;//这个top即为头指针int count = 0;//这个count代表的是当前链栈中结点的个数, 开始初始化为0个
}LinkStack;
// 其实在这里第二个结构体声明可以不用写，直接写成如下也可以：LinkStackPtr top;//但是这样写的话要注意把栈顶结点的地址赋值给topint count;//但是这里我们应该注意这个count应该设置为一个全局变量

3：栈的链式存储结构——进栈操作

// 链栈的进栈操作
int Push(LinkStack *P, ElemType e){//这个P指针指向的是包含头指针top的结构体//这个e接受的是我们想插入的数据LinkStackPtr s = (LinkStackPtr)malloc(sizeof(StackNOde));//创建一个新的结点并且为其分配空间s->data = e;//将我们想插入的数据放入新开创的结点的数据域s->next = P->top;/* 注意理解一下这里：因为栈的特性，每进栈一个数，那这个数处在栈顶的位置，而原来处在栈顶的位置的数会被新进栈的数压在底下,因此在这里我们把当前的栈顶元素赋值给新节点的直接后继 */P->top = s;//新插入的结点处在栈顶，因次让栈顶指针指向这个新结点P->count++;//结点的数量+1return OK;
}

4：栈的链式存储结构——出栈操作：

// 链栈的出栈操作
int Pop(LinkStack *P, ElemType *e){//这个P指针指向的是包含头指针top的结构体/* 这个e是来接收我们即将出栈的那个结点的数据域的数据，在这里它作为结点清楚步骤的中间变量 */LinkStackPtr temp;// 创建一个指向包含链栈结点的结构体的指针变量if(P->count == 0){//判断这个栈中结点个数是否为0，为0则说明是空栈，不可执行此操作return ERROR；//因为为空栈，不可执行出栈操作，所以返回ERROR}else{//当执行到这里时，说明链栈不为空栈，可以执行出栈操作*e = P->top->data;//注意这里是*e，因为这里不是传递地址temp = P->top;//把要即将出栈的这个栈顶结点的地址给我们出栈操作中的中间变量P->top = P->top->next;/* 让栈顶指针向下移动一位，因为这次出栈操作之后，原来处在栈顶结点下面的那个结点变成了新的栈顶结点 */free(temp);//释放我们想出栈的那个结点的空间，以防止占有内存P->count--;//结点的数量-1}return OK//执行到这一步时，说明出栈操作执行成功
}

五：栈的作用：

	有人可能会说：“用数组或者链表直接实现功能不可以吗？为什么要引入这个数据结构”	其实，栈的引入简化了程序设计的问题，划分了不同的关注层次，使得我们更加聚焦于我们要解决问题的核心，锻炼我们的思维，让我们更好的理解和学习这些数据结构，而像数组等，要分散精力去考虑数组的下标增减等细节问题，反而掩盖了问题的本质。所以现在很多的高级语言，例如JAVA、C#等都有对栈结构的封装，你可以不用关注它的实现细节，就可以直接使用Stack 的push 和 pop方法，很方便。

六：栈的应用：

1：递归：

	相信大家对递归已经有所了解了，这里不会重点讲，递归函数的定义：“一个直接调用自己或通过一系列的调用语句间接地调用自己的函数，称做递归函数”。

经典的递归例子：斐波那契数列

	下面的两端代码的功能均为打印出前40位的斐波那契数列数：

常规的迭代方法：
int main(){int i;int a[40];a[0] = 0;a[1] = 1;printf("%d ", a[0]);printf("%d ", a[1]);for(i = 2; i< 40; i++){a[i] = a[i - 1] + a[i - 2];printf("%d ", a[i]);}return 0;
}

斐波那契的递归函数：
int Fbi(int i){if( i < 2){return i == 0 ? 0 : 1;}return Fbi(i - 1) + Fbi(i - 2) /*这里函数Fbi就是调用自己，它在调用自己*/
}
int main(){int i;for(i = 0; i < 40; i++){printf("%d", Fbi(i));}return 0;
}

看了以上两端代码，迭代和递归的区别是什么呢？1：迭代使用的是循环结构，递归使用的是选择结构。递归可以使程序的结构更加的清晰、简洁、让人理解、从而减少写代码的时间。2：大量的递归调用会建立函数的副本，会耗费大量的时间和内存。跌代则不需要反复调用函数和占用额外的内存。因此我们应该视不同情况选择用不同的代码实现。

但是：说了这么多和递归的内容，和栈有什么关系呢？这要从计算
机系统内部说起

前面我们已经看到递归是如何执行它的前行和退回阶段的。递归过程退回的顺序是它
前行顺序的逆序。在退回过程中，可能要执行某些动作，包括恢复在前行过程中储存
起来的某些数据。
这种存储某些数据，然后在后面又以存储的逆序恢复这些数据，以提供之后的使用，
显然这很符合栈这样的数据结构。简单说：前行阶段，对于每一层的递归，函数的局部变量、参数值、返回地址都
被压入栈中。退回阶段，在栈顶的局部变量、参数值、返回地址被弹出，返回到需要
用到它们的代码部分，即恢复了调用的状态。对于现在的高级语言，这样的递归问题不需要用户来管理这个栈了，一切都由系统
代劳。

2: 四则运算表达式求值：

（1）：后缀（逆波兰）表示法定义（一种不需要括号的后缀表达法）：

例如：对于“9 +（3 - 1）* 3 + 10 / 2”，若用后缀表示法应该为：“9 3 1 - 3 * + 10 2 / +”
现在看不懂没有关系，下面会讲到其原理。

（2）：中缀表达式转后缀表达式：（我们把平常标准的四则运算叫做中缀表达式）

规则：
1：从左到右遍历中缀表达式的每个数字和符号，若是数字就输出，即成为后缀表达式的一部分。
2：若是符号，则判断其与栈顶符号的优先级，是右括号或优先级不高于栈顶符号
（乘除优先加减）则栈顶元素依次出栈并输出（即优先级大的要压在优先级小的头上，否则出栈并输出），并将当前符号进栈，一直到最终输出后缀表达式位置(注意：出现右括号要出栈的原因是因为要与左括号配对，即当在中缀表达式中遍历到右括号时，我们要进行出栈操作，直到将左括号出栈，两者配对并消去)。注意：1：是判断与栈顶符号的优先级。2：如果出栈的原因是因为新遍历的符号的优先级小于栈顶符号，则一直出栈至一个优先级小于这个符号的（注意是小于，不是小于等于），然后再将我们遍历到的这个符号进栈。

下面我将示例将中缀表达式9 +（3 - 1）* 3 + 10 / 2转换为后缀表达式 。

【1】：先初始化一个空栈，然后遍历中缀表达式，第一个为9，直接输出，第二个为 + 号，进栈

【2】：第三个为左括号“ ( ”,进栈，第四个为数字3，直接输出

【3】：第五个为减号“ - ”，根据上方说的规则，与栈顶符号判断，因为栈顶符号为左括号，进栈，第六个为数字1，直接输出

【4】：第七个为右括号“)”,根据规则，将栈内符号出栈，直到左括号与右括号出栈配对为止。
【5】：第八个为乘号“ * ”，优先级大于此时的栈顶符号，进栈，第九个为数字3，直接输出

【6】：第十个为加号"+“，与栈顶符号” * “比较，优先级小于” * ", 则将栈内符号出栈，直到出栈到一个小于“+”号的，但是此时栈内除了“ * ”还有“ + ”没有优先级更低的了，所以全部出栈，然后这个加号“+”再进栈。

【7】：第十一个为数字10，直接输出，第十一个为除号“ / ”,其优先级大于此时的栈顶符号“ + ”，进栈

【8】：最后一个为数字2，直接出栈，因为已经到了最后，所以将栈内的符号全部出栈并输出。最终输出的后缀表达式的结果为：

但是，我们现在会把中缀表达式转换为后缀表达式了，但是，我们要怎么对它进行计算并得出结果呢？请看下面。

（3）：后缀表达式计算结果

上面我们已经得出来了后缀表达式为：9 3 1 - 3 * + 10 2 / +

	规则：从左到右遍历后缀表达式的每个数字和符号，遇到是数字的就进栈，遇到
是符号， 就将 两个处于栈顶  的数字进行出栈  得出运算结果后进栈，一直到最后
得到最终结果。

【1】：先初始化一个空栈，然后遍历中缀表达式，第一个为数字9 ，进栈，第二个为数字3，进栈，第三个为数字1，进栈

【2】：第四个为减号“ - ”，根据规则，出栈两个栈顶的数字，其中 1 作为减数，3作为被减数（即先出栈的作为减数，后出栈的作为被减数），计算后得出的结果再进栈
【3】：第五个为数字3，进栈，第六个为乘号“ * ”，出栈两个栈顶数字得出计算结果后再进栈

【4】：第七个为加号“ + ”，出栈两个数字相加后再进栈，第八个为数字 10 ，进栈，第九个为数字 2 ，进栈，

【5】：第十个为除号“ / "出栈两个数字计算后再进栈（先出栈的作为除数，后出栈的作为被除数），最后一个为加号“+”，出栈两个数字计算后再进栈，因为是最后一个，所以最终出栈，出栈的那个数即为最终计算结果
所以，最终的计算得出的结果为20