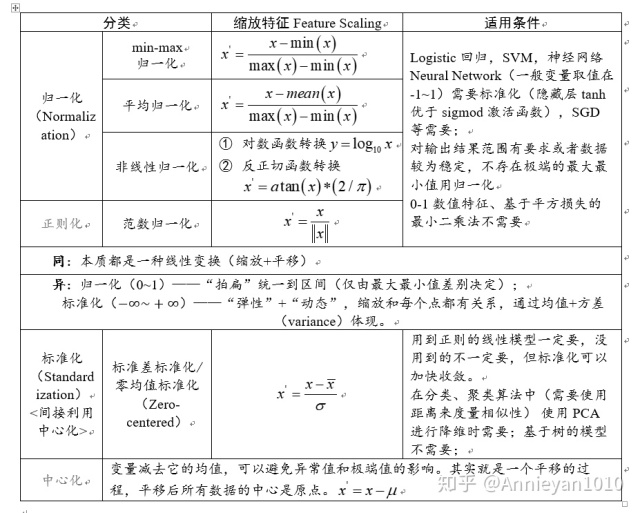
定义理解

对类、变量、方法、接口的访问范围限制。

一.类修饰符

1.直接声明 class 类名{ }，即不加修饰符的时候

这种情况下，只可访问同一包中的类，不可访问不同包中的类。

2.public，公共类的修饰符

这种情况下，既可访问同一包中的类，也可访问不同包中的类。

一个java的源文件中，规定最多只能有一个public 类。如果有public公共类，则规定文件名只能public 公共类的类名称一致，若是没有，则文件名可以任意。

3.abstract，抽象类修饰符

凡是用修饰符 abstract修饰的类，被称为抽象类。

4.final，最终类修饰符

final类是不可以被继承的。

当一个类不可能有子类时，可以用修饰符 final把它说明为最终类。

2.类成员修饰符

1.public

public修饰符表示公开的，公共的。被public修饰的成员变量和成员方法在所有类都可以访问到。

class Node
{public int e;public Node next;//用public修饰的两个成员变量。public Node(){ }public Node(int e) {this.e=e;}public Aa()//用public修饰的成员方法。{System.out.println("访问Aa方法");}
}//这个时候我们如何访问以上的成员变量和成员方法。Node node=new Node()；
//访问成员变量
node.e，node.next
//访问成员方法
node.Aa();

2.private

被private修饰的成员变量和成员方法只能在声明它们的类中访问到，而不能在其他类，包括子类，中访问到。

public class Student
{private int cj;private String name;//被private修饰的成员变量public Student( ){}public Student(int cj,String name){this.cj=cj;this.name=name;}public void set(int cj,String name){this.cj=cj;this.name=name;}
//如何访问private修饰的成员变量
//在声明类中写调用方法，如下public int getcj(){int cj=this.cj;return cj;}public String getname(){String name=this.name;return name;}
}

3.protected

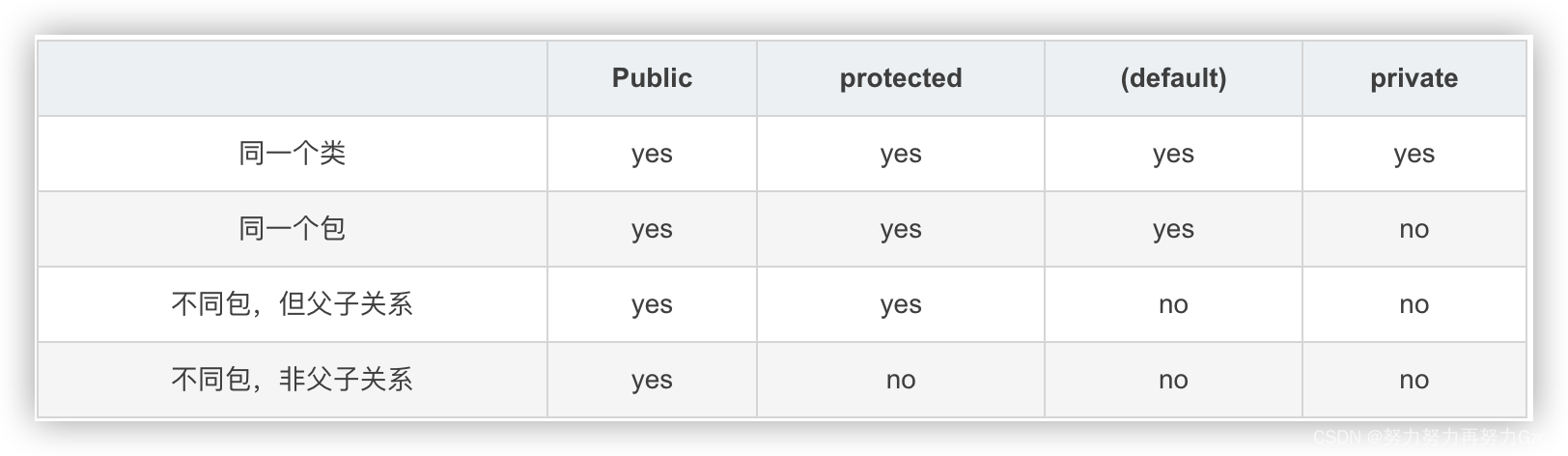
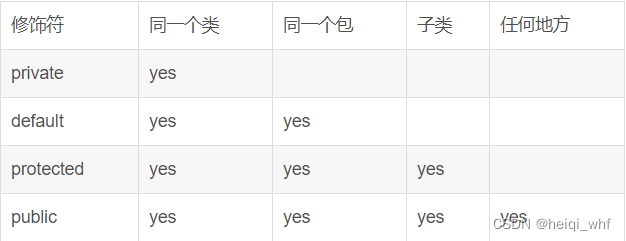
被protected修饰的成员方法和成员变量可以在声明类中访问，在该类的子类中访问，也可以在与该类位于同一包中的类访问，但不能在位于其他包的非子类中访问。

4.缺省

指不使用权限修饰符，不使用权限修饰符的成员方法和成员变量可以在声明类中访问，也可以在与该类位于同一包中的类访问，但不能在位于其他包的类中访问。