首先列一下参考文献：

[1]配电网可靠性评估方法研究现状与展望

[2]计及分布式电源的配电网供电可靠性

[3]基于仿射最小路法的含分布式电源配电网可靠性分析

[4]含电动汽车和分布式电源的配电网的可靠性评估

        之前的博客中介绍了配电网可靠性评估的三种方法、分别是解析法中的最小路法，以及序贯蒙特卡罗模拟法及非序贯蒙特卡洛模拟法：

配电网可靠性评估(二)—序贯蒙特卡洛模拟法的matlab实现

配电网可靠性评估（一）—最小路法和非序贯蒙特卡洛模拟法的matlab实现

        但是之前的内容里都没有涉及分布式电源，这篇博客主要介绍一下含分布式电源的配电网该如何进行可靠性评估。

一、引言

        分布式电源( distributed generator，DG)凭借发电方式灵活、环境污染小等优点，越来越多地被接入到配电网中，在给配电网运行方式带了变化的同时，也给配电网的可靠性带来一定的影响。DG对配电网可靠性的影响主要体现在两个方面：

        1.DG的输出具有不确定性，单凭DG并不能够保证能持续供应满足用户需求的电力；

        2.在配电网发生故障时，DG可以和周围的负荷点形成孤岛，对其恢复供电，提高系统供电可靠性。

        另外，根据对DG建模的方法不同，通常采用的可靠性评估方法也不一样。在含DG的配电网可靠性评估中，DG的数学模型主要包括概率模型和时序模型，两种模型的基本原理如下：

1.概率模型

        这里的说的概率模型不是通常数学意义上的那种概率密度函数，而是通过计算得到DG不同出力对应的概率。最简单的概率模型就是两状态模型，假设DG额定功率运行的概率是P1，停运的概率是P2，满足P1+P2=1就行。再复杂一些的可以设计为多状态模型，比如参考文献[3]里面就设计了一种四状态模型，以各状态间的转移概率表征DG出力的波动，通过马尔可夫状态转移法求出各状态的概率，进一步确定出孤岛形成的概率。采用概率模型对DG进行建模时，可靠性评估方法一般就采用解析法或非序贯蒙特卡罗模拟法，在进行可靠性评估时，首先根据概率确定分布式电源的出力大小，再根据DG出力确定孤岛划分以及负荷的供应情况即可统计出可靠性指标。

2.时序模型

        时序模型就是要得到DG按时间顺序变化的输出功率大小。很多时候都采用典型的变化曲线即可，也就是历史的变化曲线或者是预测的曲线，一般都是以1小时为时间间隔，一年则需要8760个采样点。也有一些文献根据历史参数拟合DG出力概率密度函数的参数，再根据概率密度函数来生成一些典型的场景。采用时序模型对DG进行建模时，可靠性评估方法一般就采用序贯蒙特卡洛模拟法，进行仿真的时候根据仿真的时长就可以确定分布式电源的出力大小，再根据DG出力确定孤岛划分以及负荷的供应情况即可统计出可靠性指标。

二、基本步骤

        博客里以DG的概率模型+最小路法，以及DG的时序模型+序贯蒙特卡洛模拟法为例，介绍含DG的配电网可靠性评估的步骤。

1.概率模型+最小路法

        以文献[3]中提到的四状态概率模型，加上我自己之前的博客里提到的最小路法进行含DG的配电网可靠性评估步骤如下：

step1:建立DG输出功率的概率模型

        将DG视为一个具有若干容量状态的发电机，假设包含全额发电、两个降额运行以及全额停运四个状态。以各状态间的转移概率表征DG出力的波动，通过马尔可夫状态转移法求出各容量状态概率。系统在状态转态无关。采用Si表示第i个输出功率水平(S1>S2 >S3>S4),aij表示输出功率从Si转移到Sj的状态转移概率。所建立的发电机多容量状态模型如下所示。

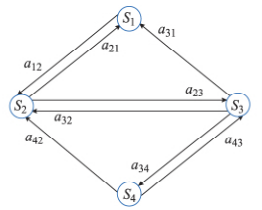
        以矩阵A'表示DG的马尔可夫状态转移概率。根据图1的状态空间,可以得到系统的状态转移率矩阵为：

step2：求负荷k到主电源节点的最短路径

        可采用Dijkstra算法，Bellman-Ford算法，Floyd算法和SPFA算法等最短路径的算法求出负荷节点到主电源节点的最短路径，并确定路径中包含的元件；

step3：判断元件故障对负荷k的影响

        根据有无备用电源、有无分段装置、有无熔断器保护、元件是否在负荷的最小路上判断各个元件故障对负荷k的影响，这里不再赘述，可以参考我之前的博客以及文献[2]；

step4：判断孤岛形成条件

        假设在不含DG的情况下，某个元件m故障会使负荷k发生故障，这时候需要根据故障的位置，负荷的位置，开关动作以及DG的输出功率等条件判断是否可以通过DG形成孤岛对负荷k恢复供电，并根据DG各个出力的概率求出孤岛形成的概率。进行孤岛划分时，一般采用广度优先的原则进行孤岛划分，同时需要满足连通性约束与功率平衡约束。以下图为例进行说明：

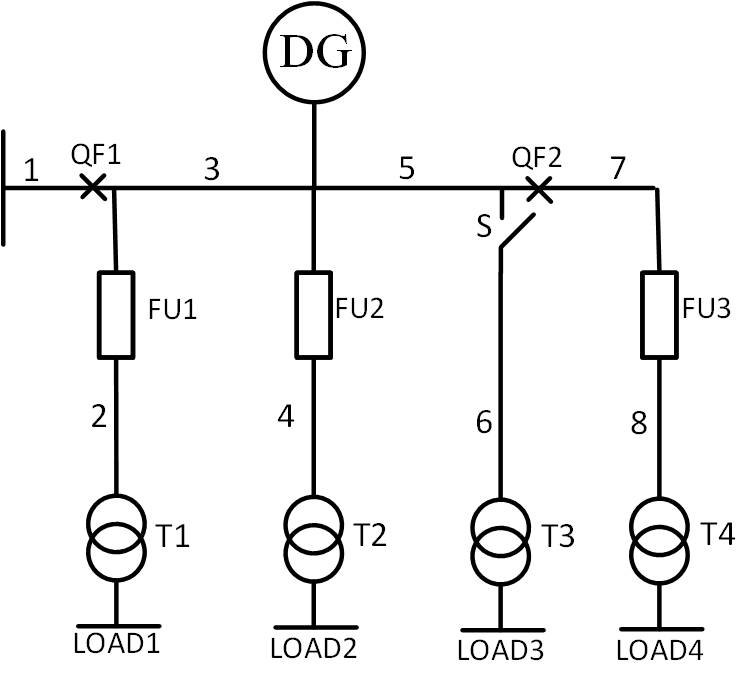
         假设图中DG四个状态分别为[S1 S2 S3 S4]=[0 100 200 300]kW，出现概率均为0.25，负荷1-4均为100kW。

       如果线路3处发生故障，断路器QF1断开，此时只要DG出力达到一定要求，就可以形成孤岛，恢复对负荷2-4的供电。当状态为S2、S3、S4时，可以恢复对负荷2的供电，也就是在线路3故障时负荷2由DG恢复供电的概率为0.75；当状态为S3、S4时，可以恢复对负荷3的供电，也就是在线路3故障时负荷3由DG恢复供电的概率为0.5；当状态为S4时，可以恢复对负荷4的供电，也就是在线路3故障时负荷4由DG恢复供电的概率为0.25。这是DG出力的不同导致孤岛划分不同。

        另外，故障位置也会影响孤岛的形成。假设线路5处发生故障，断路器QF1断开，此时无论DG出力在什么状态，最多只能恢复对负荷2的供电。这是因为线路5的故障导致DG无法和负荷3及负荷4形成供电回路，无法满足孤岛形成的连通性约束。

        综上，这一步骤需要判断不同情况下形成孤岛对负荷k恢复供电的概率。

step5：累加负荷可靠性指标

        根据上述计算累计负荷的年平均故障率、年平均故障时间以及平均年失负荷等可靠性指标；

step6：迭代终止判断

        如果统计完所有负荷的可靠性指标，则进行下一步，否则令k=k+1然后返回步骤2；

step7：统计系统可靠性指标

        根据所有负荷节点的可靠性指标，统计系统的可靠性指标。

2.时序模型+序贯蒙特卡洛模拟法

        以DG的时序模型为基础，加上我自己之前的博客里提到的序贯蒙特卡洛模拟法进行含DG的配电网可靠性评估步骤如下：

step1:建立DG输出功率的时序模型

        可以像文献[4]中一样，写出DG的出力概率密度函数，再经过抽样得到DG的时序出力变化，具体过程如下：

        也可以采用历史数据，效果大差不大。为简单起见，这里就直接采用历史数据。

step2：初始化仿真参数 

        读取设备的可靠性参数，初始化仿真年限；

step3：确定故障设备和故障时间

        计算每个设备的正常工作时间TTF，利用一定规则确定故障的设备与故障的时间，一般都是假定TTF最小的设备为本次模拟时发生故障的设备；

step4：确定受影响负荷

        根据故障元件的位置，各个负荷所处的位置，开关的动作状态以及DG的出力大小等因素确定本次故障导致停运的负荷，并统计停运时间和失负荷量。孤岛的形成在要这一步骤进行考虑，划分的依据和上面一样；

step5：迭代终止判断

        将系统仿真时间加上TTF和故障持续时间，判断是否达到仿真阈值，若是则进行下一步，否则返回步骤3；

step6：可靠性统计

        统计各个负荷节点的可靠性指标以及系统平均可靠性指标。

三、运行结果

    采用IEEE RBTS BUS6 F4作为算例，假设有两个DG分别接在图示的位置，分别采用两种方法进行可靠性评估，并进行对比分析。

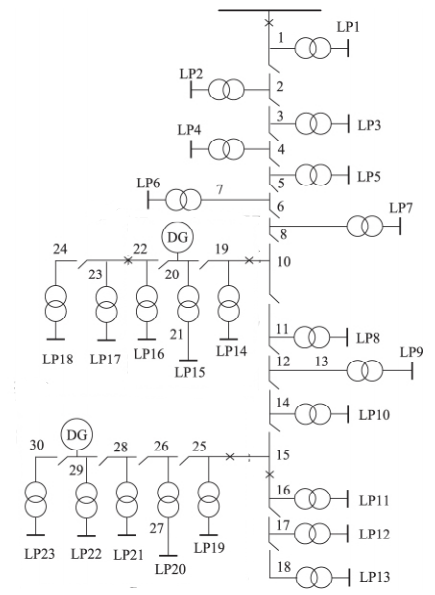
1.概率模型+最小路法

        假设两个DG的出力状态均为S=[0,240,640,800]kW，可靠性评估的结果如下：

 

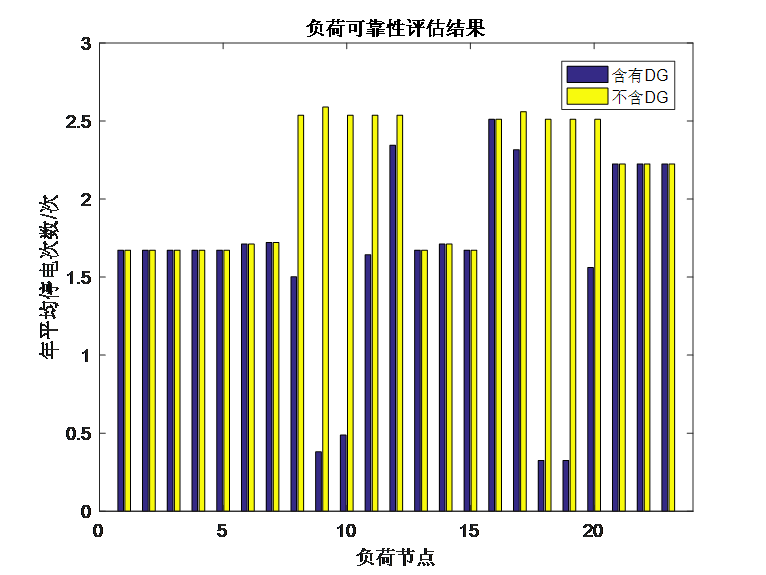
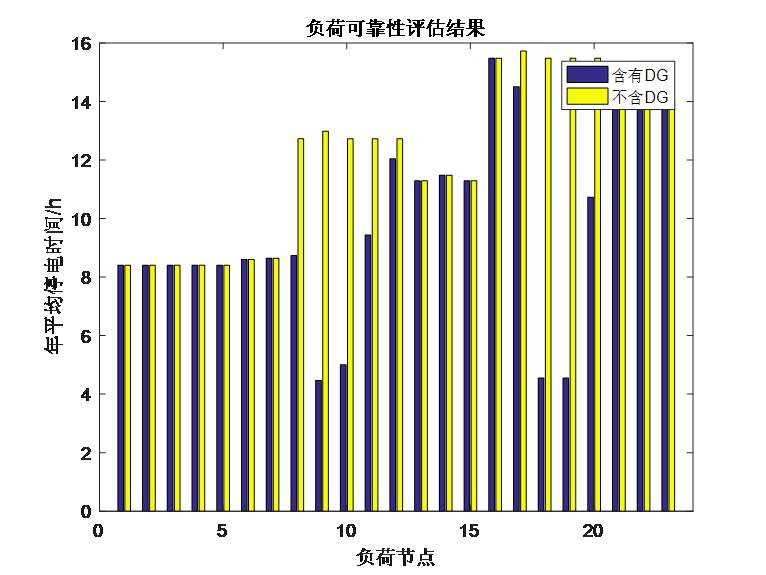
        由结果可知，在DG接入点附近的负荷，部分故障发生时可以形成孤岛供电，因此年平均停电次数和年平均停电时间均有非常明显的改善，系统整体可靠性指标也因此有了比较明显的改善。

2.时序模型+序贯蒙特卡洛模拟法

        假设两个DG的额定功率均为800kW，采用光伏输出功率的历史数据作为DG的时序模型，可靠性评估的结果如下：

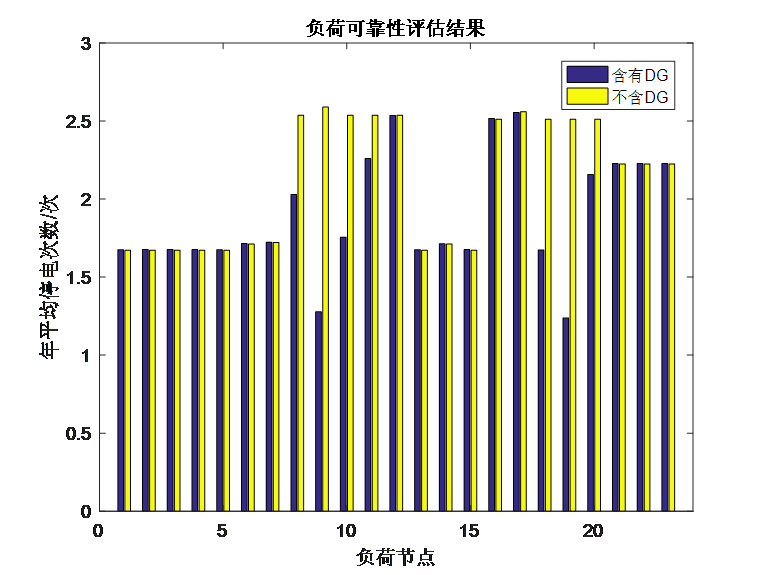
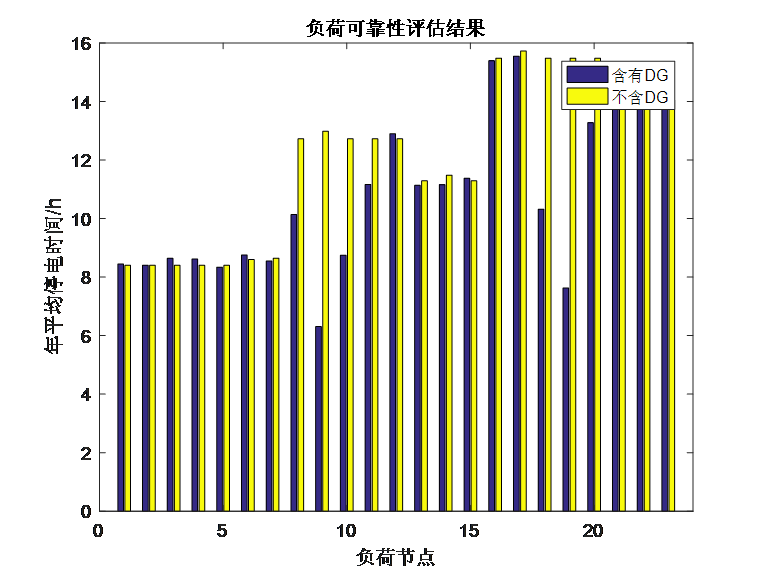
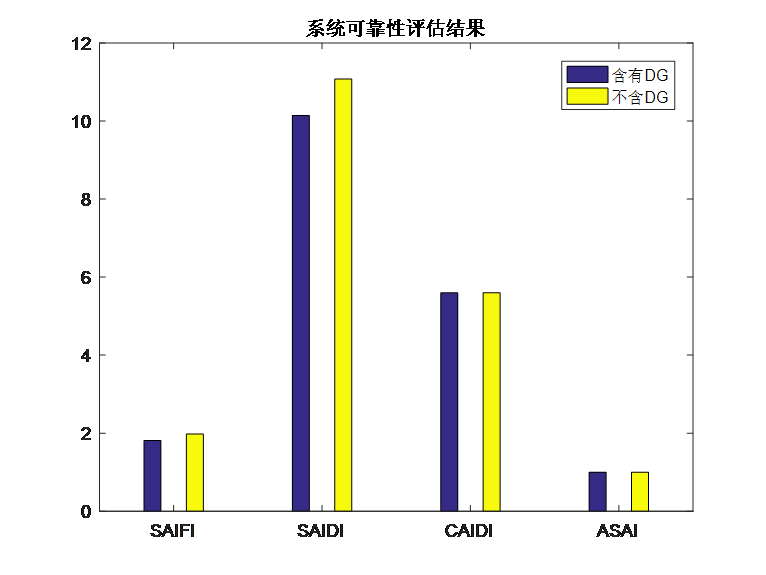
         由结果可知，采用时序模型+序贯蒙特卡洛模拟法对DG进行建模，也是DG接入点附近的负荷可靠性指标有比较大的改善，但是改善幅度并没有像概率模型那么大。实际上，采用时序模型比概率模型还是要精确一些的，直接把DG等同于只有几个状态的发电机也太粗糙了。

 四、matlab代码

1.概率模型+最小路法

        采用概率模型+最小路法进行含DG的配电网可靠性评估部分matlab代码如下：

clc
clear
close all
% 读取数据
[line_num,line,load_num,load] = IEEE_RBTS_BUS6_F4;%可以自己修改参数
% 生成图
g=graph(line(:,1),line(:,2),line(:,3));
% plot(g)%生成节点图
% DG接入位置，可修改
DG_position=[13,27];
% 初始化负荷点可靠性指标
Lambda_load=zeros(1,load_num);
Gamma_load=zeros(1,load_num);
U_load=zeros(1,load_num);
P_load=zeros(1,load_num);
load_users=zeros(1,load_num);
% DG四状态概率模型,DG出力大小可以自己修改,如果四个状态均为零就相当于不含DG的系统
[P1,S1]=DG_probability_model(0,240,640,800);
[P2,S2]=DG_probability_model(0,240,640,800);
% 各个状态下可形成孤岛供电的负荷及恢复比例
node_island1=cell(2,4);
node_island2=cell(2,4);
% 可恢复负荷的搜索顺序
search_order1=[9 10 8 11 12 7 13 6];
search_order2=[19 18 20 17 16 15 14];
% 确定可以形成孤岛的负荷
for k=1:4省略...
end
for k=1:load_num省略...
end
SAIFI=Lambda_load*(load_users')/(sum(load_users));
EENS=sum(P_load);
SAIDI=U_load*(load_users')/(sum(load_users));
CAIDI=SAIDI/SAIFI;
ASAI=1-SAIDI/8760;
Lambda_load0=[1.6725 	1.6725 	1.6725 	1.6725 	1.6725 	1.7115 	1.7213 	2.5370 	2.5890 	2.5370 	2.5370 	2.5370 	1.6725 	1.7115 	1.6725 	2.5110 	2.5598 	2.5110 	2.5110 	2.5110 	2.2250 	2.2250 	2.2250 ];
U_load0=[8.4015 	8.4015 	8.4015 	8.4015 	8.4015 	8.5965 	8.6453 	12.7240 	12.9840 	12.7240 	12.7240 	12.7240 	11.2875 	11.4825 	11.2875 	15.4800 	15.7238 	15.4800 	15.4800 	15.4800 	14.0500 	14.0500 	14.0500 ];
SAIFI0=1.97781318681319;
SAIDI0=11.074659340659341;
CAIDI0=5.599446608253094;
ASAI0=0.998735769481660;
EENS0=57.7903811000000;
figure
bar(1:23,[Lambda_load;Lambda_load0]')
xlim([0,24])
title('负荷可靠性评估结果')
xlabel('负荷节点');ylabel('年平均停电次数/次');
legend('含有DG','不含DG')
figure
bar(1:23,[U_load;U_load0]')
xlim([0,24])
title('负荷可靠性评估结果')
xlabel('负荷节点');ylabel('年平均停电时间/h');
legend('含有DG','不含DG')
Z=[SAIFI SAIDI CAIDI ASAI;SAIFI0 SAIDI0 CAIDI0 ASAI0]';
figure(3)
bar(Z,0.4)
title('系统可靠性评估结果')
set(gca,'XTickLabel',{'SAIFI','SAIDI','CAIDI','ASAI'});
legend('含有DG','不含DG')
disp('**************含DG配电网可靠性指标**************')
disp(['SAIFI=',num2str(SAIFI),'次/（年·户）'])
disp(['SAIDI=',num2str(SAIDI),'小时/（年·户）'])
disp(['EENS=',num2str(EENS),'MW/（年·户）'])
disp(['ASAI=',num2str(ASAI*100),'%'])
disp('**************不含DG配电网可靠性指标**************')
disp(['SAIFI=',num2str(SAIFI0),'次/（年·户）'])
CAIDI=SAIDI/SAIFI;
disp(['SAIDI=',num2str(SAIDI0),'小时/（年·户）'])
disp(['EENS=',num2str(EENS0),'MW/（年·户）'])
disp(['ASAI=',num2str(ASAI0*100),'%'])

2.时序模型+序贯蒙特卡洛模拟法

        采用时序模型+序贯蒙特卡洛模拟法进行含DG的配电网可靠性评估部分matlab代码如下：

clc
clear
close all
%% 序贯蒙特卡洛模拟法，假设DG为光伏发电，采用历史数据构建时序模型，以1小时为采样间隔
%% 读取数据
[line_num,line,load_num,Pload] = IEEE_RBTS_BUS6_F4;% 配电网参数
load('pv_data.mat');% 光伏参数
%% DG接入位置，可修改
DG_position=[13,27];
%% DG容量,可修改
P_pv=[800,800]/1000;
%% 可恢复负荷的搜索顺序
search_order1=[9 10 8 11 12 7 13 6];
search_order2=[19 18 20 17 16 15 14];
%生成图
g=digraph(line(:,1),line(:,2),line(:,3));
%% 利用节点网络分析法确定影响负荷的元件
node_analyse;
%% 序贯蒙特卡洛法
load_users=Pload(:,5);
load_fault=zeros(1,load_num);%故障次数
load_fault_time=zeros(1,load_num);%故障时间
load_power=zeros(1,load_num);%失负荷量
Lambda=(line(:,3).*line(:,4))';
Gamma1=line(:,5);
Gamma2=line(:,8);
power=Pload(:,3);
N=1000;%仿真的年数
time=0;%初始化仿真时间
load_normal=zeros(1,load_num);%正常工作时间
while time<N*8760省略...
end
Lambda_load0=[1.6725 	1.6725 	1.6725 	1.6725 	1.6725 	1.7115 	1.7213 	2.5370 	2.5890 	2.5370 	2.5370 	2.5370 	1.6725 	1.7115 	1.6725 	2.5110 	2.5598 	2.5110 	2.5110 	2.5110 	2.2250 	2.2250 	2.2250 ];
U_load0=[8.4015 	8.4015 	8.4015 	8.4015 	8.4015 	8.5965 	8.6453 	12.7240 	12.9840 	12.7240 	12.7240 	12.7240 	11.2875 	11.4825 	11.2875 	15.4800 	15.7238 	15.4800 	15.4800 	15.4800 	14.0500 	14.0500 	14.0500 ];
SAIFI0=1.97781318681319;
SAIDI0=11.074659340659341;
CAIDI0=5.599446608253094;
ASAI0=0.998735769481660;
EENS0=57.7903811000000;
%负荷停电次数
Lambda_load=load_fault./load_normal;
%负荷停电时间
Gamma_load=load_fault_time./load_fault;
U_load=Lambda_load.*Gamma_load;
figure
bar(1:23,[Lambda_load;Lambda_load0]')
xlim([0,24])
title('负荷可靠性评估结果')
xlabel('负荷节点');ylabel('年平均停电次数/次');
legend('含有DG','不含DG')
figure
bar(1:23,[U_load;U_load0]')
xlim([0,24])
title('负荷可靠性评估结果')
xlabel('负荷节点');ylabel('年平均停电时间/h');
legend('含有DG','不含DG')
Z=[SAIFI SAIDI CAIDI ASAI;SAIFI0 SAIDI0 CAIDI0 ASAI0]';
figure(3)
bar(Z,0.4)
title('系统可靠性评估结果')
set(gca,'XTickLabel',{'SAIFI','SAIDI','CAIDI','ASAI'});
legend('含有DG','不含DG')
disp('**************含DG配电网可靠性指标**************')
disp(['SAIFI=',num2str(SAIFI),'次/（年·户）'])
disp(['SAIDI=',num2str(SAIDI),'小时/（年·户）'])
disp(['EENS=',num2str(EENS),'MW/（年·户）'])
disp(['ASAI=',num2str(ASAI*100),'%'])
disp('**************不含DG配电网可靠性指标**************')
disp(['SAIFI=',num2str(SAIFI0),'次/（年·户）'])
CAIDI=SAIDI/SAIFI;
disp(['SAIDI=',num2str(SAIDI0),'小时/（年·户）'])
disp(['EENS=',num2str(EENS0),'MW/（年·户）'])
disp(['ASAI=',num2str(ASAI0*100),'%'])

这上面提供的是部分的代码，要获取完整代码可以戳这里：

含分布式电源的配电网可靠性评估的matlab实现