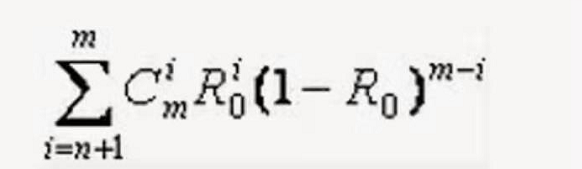计算机组成原理-计算机可靠性模型
计算机系统是一个复杂的系统,影响可靠性的因素非常多,难以进行直接可靠性分析,但通过建立适当数学模型,把大系统分割为若干子系统,可简化其分析过程,以下是三种常见的系统可靠性数学模型
可靠性R
指从它开始运行到某个时刻这段时间内能正常运行的概率
失效率λ
指单位时间内失效的元件数与元件总数的比例
串联系统
假设一个系统由N个子系统组成,当且仅当所有子系统都能正常工作时系统才能正常工作
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-r6uGB5Gi-1572851902304)(C:\Users\JunSIr\AppData\Roaming\Typora\typora-user-images\image-20191104145041382.png)]](https://img-blog.csdnimg.cn/20191104151901717.png)
可靠性R计算
假设各个子系统的可靠性分别用R1R2…表示,则系统可靠性为
R = R 1 R 2... R n R = R1R2...Rn R=R1R2...Rn
失效率λ 计算
假设各个子系统的可靠性分别用λ 1λ 2…表示,则系统可靠性为
λ = λ 1 + λ 2 + . . . . + λ 3 λ = λ 1+λ 2+....+λ 3 λ=λ1+λ2+....+λ3
系统越多可靠性越差,失效率也越大
并联系统
假设一个系统由N个子系统组成,只要有一个子系统正常工作时系统就能正常工作
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-JLcMBUFt-1572851902305)(C:\Users\JunSIr\AppData\Roaming\Typora\typora-user-images\image-20191104145929253.png)]](https://img-blog.csdnimg.cn/201911041519197.png)
可靠性R计算
假设各个子系统的可靠性分别用R1R2…表示,则系统可靠性为
R = 1 − ( 1 − R 1 ) ( 1 − R 2 ) . . . ( 1 − R n ) R = 1-(1-R1)(1-R2)...(1-Rn) R=1−(1−R1)(1−R2)...(1−Rn)
若是相同子系统
R = 1 − ( 1 − R ) 的 n 次 方 R=1-(1-R)的n次方 R=1−(1−R)的n次方
失效率λ 计算
串并联混合系统
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-cXtrelwO-1572851902306)(C:\Users\JunSIr\AppData\Roaming\Typora\typora-user-images\image-20191104151049300.png)]](https://img-blog.csdnimg.cn/20191104151933569.png)
可靠度R计算
若每个子系统可靠度均为R
系统可靠度为
R(1-(1-R)的平方)(1-(1-R)的平方) = R(1-(1-R)的平方)的平方