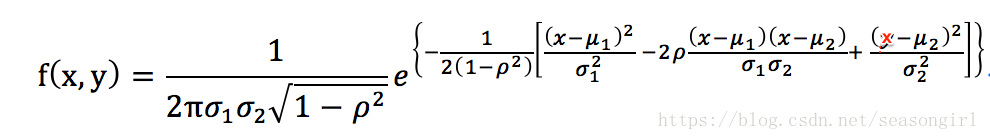1、多维高斯分布的概率密度函数
多维变量 X = ( x 1 , x 2 , . . . x n ) X=(x_1,x_2,...x_n) X=(x1,x2,...xn)的联合概率密度函数为:
![f(X)=1(2π)d/2|Σ|1/2exp[−12(X−u)TΣ−1(X−u)],X=(x1,x2...xn)f(X)=1(2π)d/2|Σ|1/2exp[−12(X−u)TΣ−1(X−u)],X=(x1,x2...xn)](https://img-blog.csdnimg.cn/20200722103805544.png)
其中:
d:变量维度。对于二维高斯分布,有d=2;
u = ( u 1 u 2 … u n ) u=(u_1 u_2 … u_n) u=(u1u2…un):各位变量的均值;
Σ:协方差矩阵,描述各维变量之间的相关度。对于二维高斯分布,有:
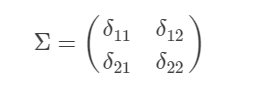
后文主要分析均值和协方差矩阵对二维高斯分布的影响。
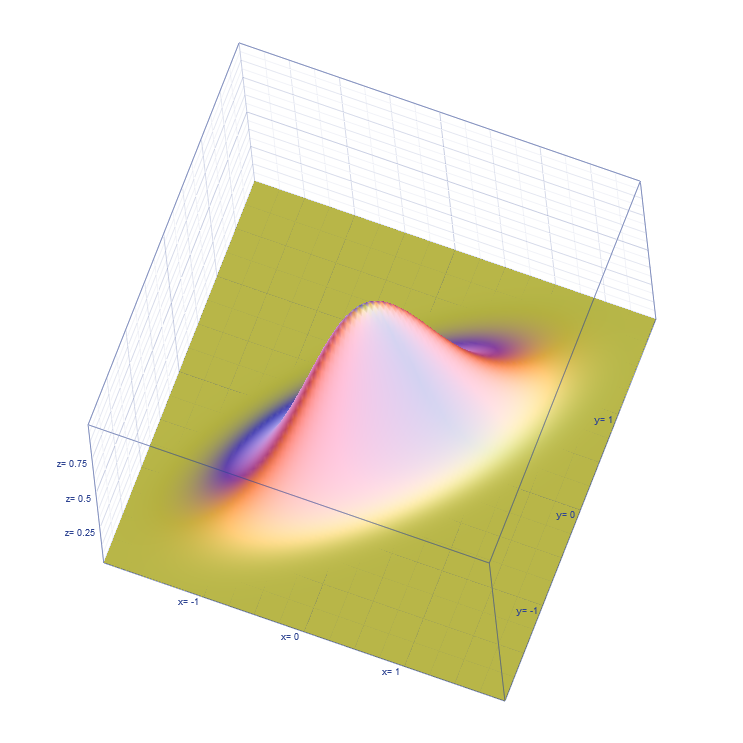
2、均值和协方差矩阵对二维高斯分布的影响
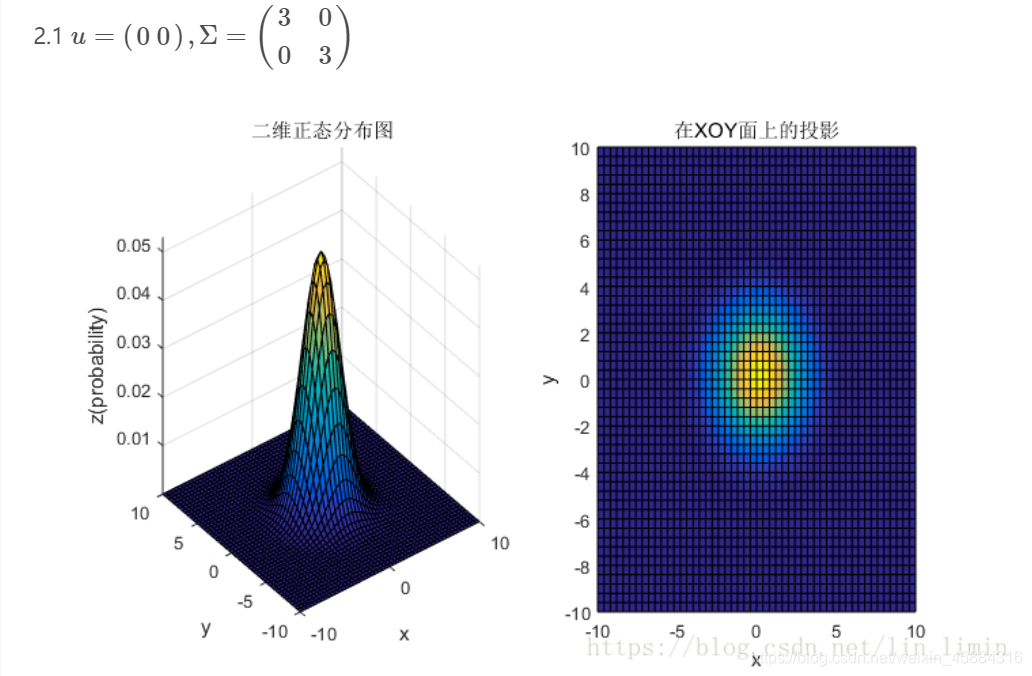
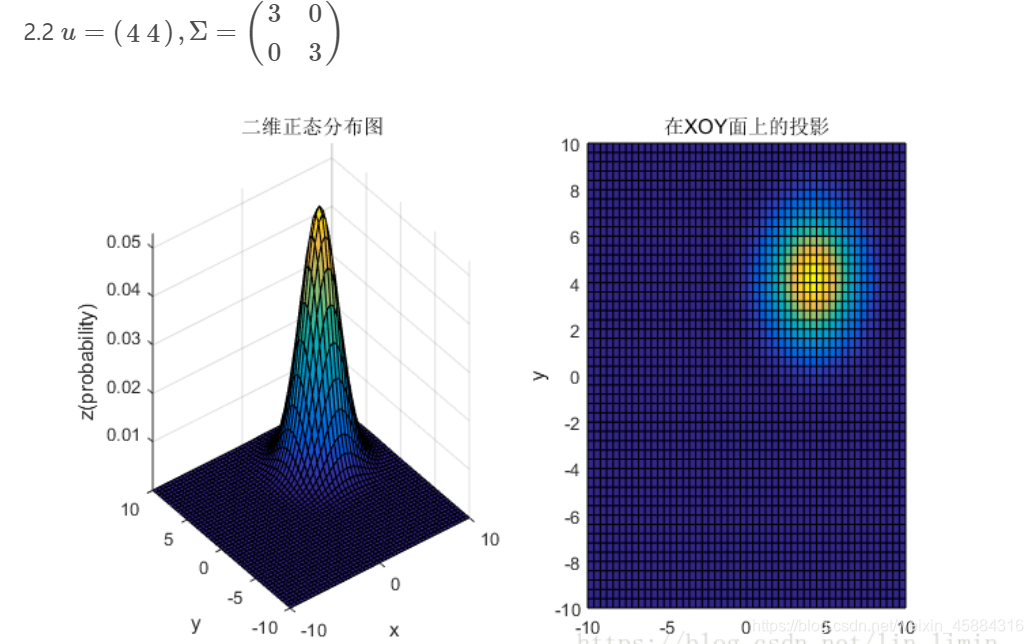
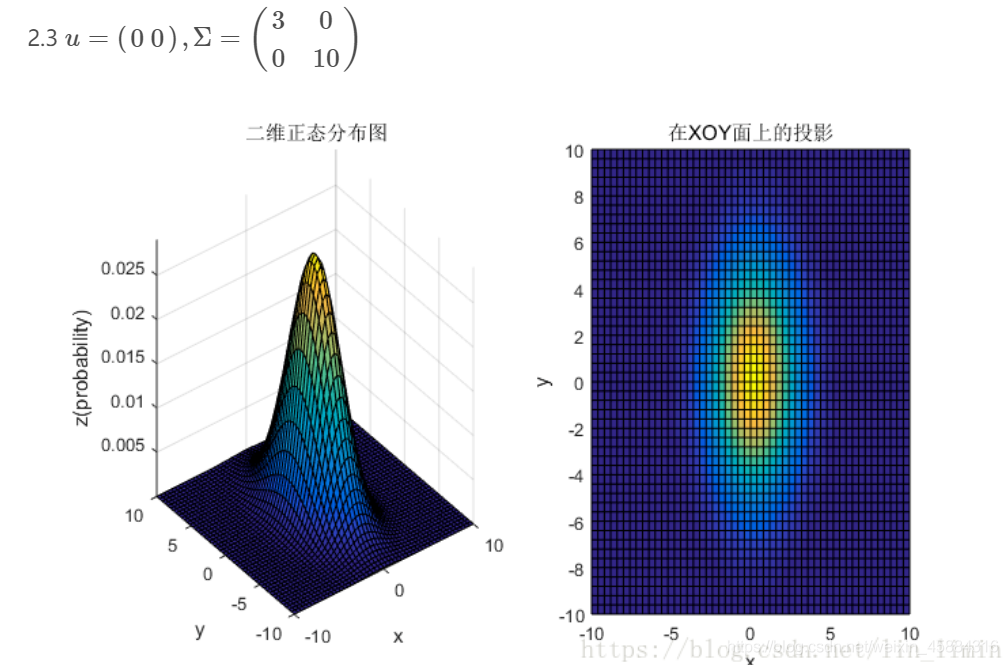
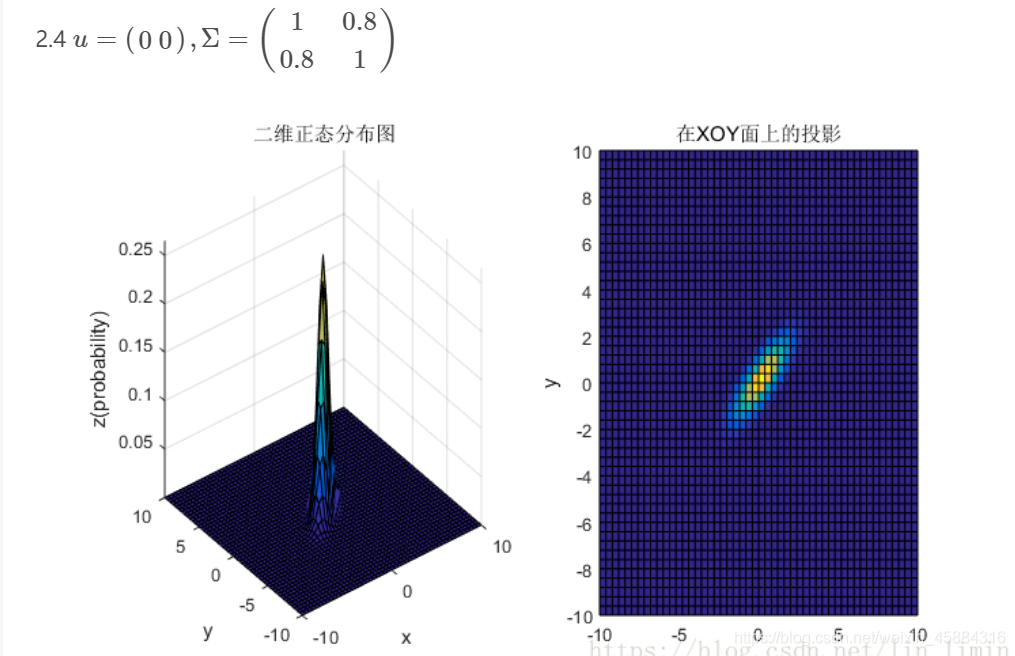
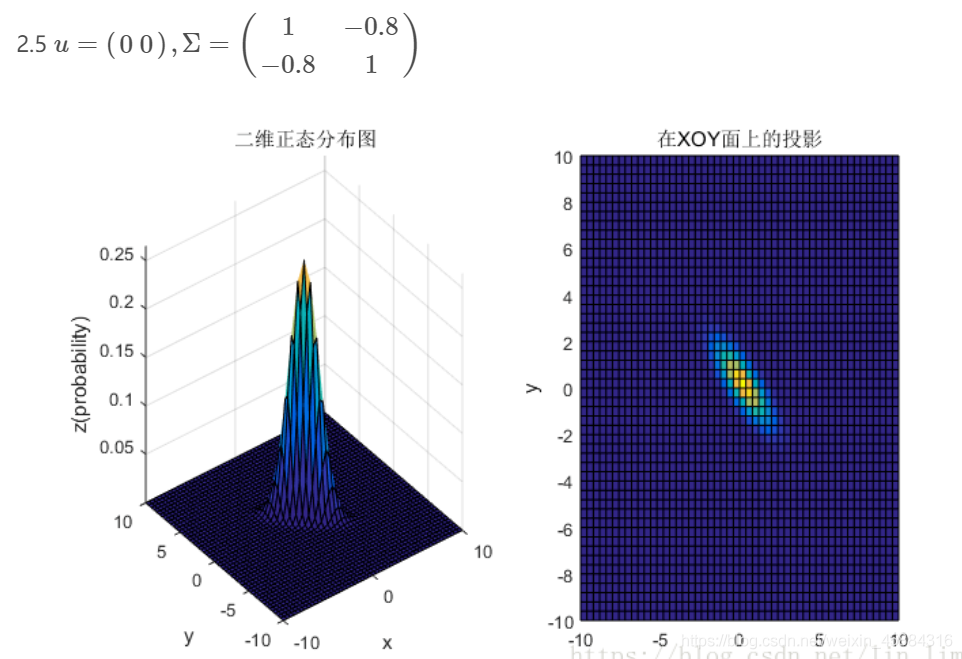
3、总结
①均值表征的是各维变量的中心,其对二维高斯曲面的影响较好理解,它使得整个二维高斯曲面在xoy平面上移动;
②对于协方差矩阵,对角线上的两个元素,即 δ 11 \delta _{11} δ11和 δ 22 \delta _{22} δ22表征的是x维和y维变量的方差,决定了整个高斯曲面在某一维度上的“跨度”,方差越大,“跨度”越大;
③协方差矩阵的斜对角线上面的两个元素,即 δ 12 \delta _{12} δ12和 δ 21 \delta _{21} δ21表征的是各维变量之间的相关性:δ12δ12>0说明x与y呈正相关(x越大,y越大),其值越大,正相关程度越大; δ 12 \delta _{12} δ12<0呈负相关;否则不相关。
————————————————
版权声明:本文为CSDN博主「林立民爱洗澡」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/lin_limin/article/details/81024228