碰撞检测

碰撞检测是3维游戏内必不可少的一个功能，有了碰撞检测，游戏才能显得更加真实。之前查找碰撞检测的资料，很多都提到了SAT以及GJK算法，但是少有对这两个算法进行深入解析的。于是本人花了一个星期左右去阅读GJK的论文，现在将论文内的细节进行整理，和大家分享。碰撞检测涉及到相当多数学知识，所以这个主题应该会有好几个部分组成。文章内可能会出现一些错的或者是不严谨的地方，也还请大家指正
论文地址：http://web.eecs.umich.edu/~grizzle/GilbertFest/Gilbert(58).pdf
论文的第一部分是总结前人工作以及对不同算法的比较，不涉及算法内容，因此跳过，直接从第二部分开始。还有一点是，公式后面的标号会和论文对应，所以可能不按顺序。

Objcet Representation And Distance

1.涉及的概念

• 紧集（compact sets）：紧集是指拓扑空间内的一类特殊点集，它们的任何开覆盖都有有限子覆盖。举个例子，实数的闭区间[a, b]即为紧集，而有理数的闭区间[c, d]不为紧集，这是因为实数是紧的，而有理数不是紧的。另一种表述是，如果一个有理数序列，其项为3，3.14，3.141，1.1415…可以知道，这个序列的极限是π，但是π不是有理数，也就是说由有理数构成的序列的极限可能不属于有理数，那么有理数的数轴上存在着无数的“洞”，既然有洞，那么肯定就不紧致。如果一个集合是紧的，那么它肯定是有界的。
• 欧几里得距离（Euclidean length）：欧几里得空间的度量函数，其实就是我们常用的计算向量长度的公式
• 凸多面体（convex polytopes）：简单来说就是如果一个多面体内任意两点之间的线段都包含在这个多面体内，那么这个多边形就是凸多面体。GJK算法适用于凸多面体，不适用与凹多面体（但是可以将凹多面体拆成多个凸多面体）。

2.内容详解

假设现在存在两个三维空间内的紧集$K_A,K_B\in R^3$，然后定义如下符号：
d ( K A , K B ) = m i n { ∣ x − y ∣ : x ∈ K A , y ∈ K B } ( 1 ) d(K_A, K_B ) = min \lbrace |x - y|: x \in K_A, y \in K_B \rbrace \kern3em \lparen1\rparen d(KA​,KB​)=min{∣x−y∣:x∈KA​,y∈KB​}(1)显然，上式表示的是这两个集合中最近的点的距离，下图线段cd的长度就代表了两个圆最短的距离（为了画图方便，这里用了二维的图）

如果集合A和B是由多个子集构成，这些子集满足：
$$K_A=\bigcup _{i\in I_A}{K}_i{K}_B=\bigcup _{j\in I_B}{K}_j(2)$$其中$I_A$和$I_B$是索引集(index set)。按照（1）式的定义，有：
d ( K A , K B ) = m i n { d i j : i ∈ I A , j ∈ I B } ( 3 ) d(K_A, K_B ) = min \lbrace d_{ij}: i \in I_A, j \in I_B \rbrace \kern3em \lparen3\rparen d(KA​,KB​)=min{dij​:i∈IA​,j∈IB​}(3)其中$d_{ij}$定义为：
d i j = m i n { ∣ x − y ∣ : x ∈ K i , y ∈ K j } ( 4 ) d_{ij} = min \lbrace |x - y|: x \in K_i, y \in K_j \rbrace \kern4em \lparen4\rparen dij​=min{∣x−y∣:x∈Ki​,y∈Kj​}(4)即$d_{ij}$表示的是子集$K_i$和$K_j$之间的最短距离，然后返回公式（3）可得，两个集合之间的最短距离是各自子集最短距离的最小值。论文中的图很好的表现了这一点，这里我不作过多阐述。

接下来是r-球面扩展。举两个例子，三维空间中，点的r-球面扩展就是一个球，线段的r-球面扩展就是两头为球面的圆柱(上图中的$K_2$)，这里的r指的是半径。其公式如下：
K r = { x : ∣ x − y ∣ ⩽ r , y ∈ K } ( 5 ) K^r = \lbrace x: |x - y| \leqslant r, y \in K\rbrace \kern3em \lparen5\rparen Kr={x:∣x−y∣⩽r,y∈K}(5)显然，在进行球面扩展之后两个闭集的最短距离可以表示为：
$$d(K_A^{r_A},K_B^{r_B})=(d(K_A,K_B)-r_A-r_B)+(6)$$其中+号是代表当值小于0时，值取0。
如果将公式（2）中的子集变成是球面扩展，那么结合公式（4）和公式（6）可得：
d ( K A , K B ) = m i n { ( d i j − r i − r j ) + : i ∈ I A , j ∈ I B } ( 8 ) d(K_A, K_B ) = min \lbrace (d_{ij} - r_i - r_j)+: i \in I_A, j \in I_B \rbrace \kern3em \lparen8\rparen d(KA​,KB​)=min{(dij​−ri​−rj​)+:i∈IA​,j∈IB​}(8)球面扩展可以在不少地方进行应用，像是要加壳的零件等。公式（8）提供了一个便利的计算方式。
接下来是讲当集合需要进行变换时该怎么处理。球面扩展和变换都稍微有点发散，所以这里不展开讲，有需要的话我在后面再进行补充。

Preliminaries

1.涉及的概念

• 仿射集、仿射包、凸集、凸包、锥：具体的概念参考这篇文章：凸优化1——仿射集、凸集、锥。这几个概念相当重要，如果是想透彻地了解这个算法，那么必须弄懂这几个概念及其数学的表达
• Minkowski difference(sum)：这个概念并不复杂，如果有两个集合A和B，那么它们的Minkowski sum就是集合 { x A + x B , x A ∈ A , x B ∈ B } \lbrace x_A + x_B, x_A \in A, x_B \in B \rbrace {xA​+xB​,xA​∈A,xB​∈B}，Minkowski difference就是集合 { x A − x B , x A ∈ A , x B ∈ B } \lbrace x_A - x_B, x_A \in A, x_B \in B \rbrace {xA​−xB​,xA​∈A,xB​∈B}

2.内容详解

在这个小节里，集合X表示m维空间内的紧集，而Y表示m维空间的有限集，即Y中包含有限个顶点。那么集合X的仿射包表示为：
a f f X = { ∑ i = 1 l λ i x i , x i ∈ X , λ 1 + . . . + λ l = 1 } ( 11 ) aff X= \lbrace \sum_{i = 1}^l \lambda^ix_i,x_i \in X, \lambda^1 + ... + \lambda^l = 1 \rbrace \kern3em \lparen11\rparen affX={i=1∑l​λixi​,xi​∈X,λ1+...+λl=1}(11)而集合X的凸包为：
c o X = { ∑ i = 1 l λ i x i , x i ∈ X , λ i ⩾ 0 , λ 1 + . . . + λ l = 1 } ( 12 ) coX= \lbrace \sum_{i = 1}^l \lambda^ix_i,x_i \in X,\lambda^i\geqslant 0 , \lambda^1 + ... + \lambda^l = 1 \rbrace \kern3em \lparen12\rparen coX={i=1∑l​λixi​,xi​∈X,λi⩾0,λ1+...+λl=1}(12)式（11）和式（12）只差了一个条件：凸包将系数${\lambda }^i$限定为大于0。从上面的定义可以看出，$affX$是一个线性空间的平移。首先需要明确线性空间这个概念，线性空间也称为向量空间，具体的定义可以参考百度百科：向量空间。为什么说是平移，举个例子， a f f Y = Y + { y 1 } affY = \bold{Y} + \lbrace y_1 \rbrace affY=Y+{y1​}，其中 Y = { y 2 − y 1 , y 3 − y 1 , . . . , y v − y 1 } \bold{Y} = \lbrace y_2-y_1, y_3-y_1, ...,y_v-y_1 \rbrace Y={y2​−y1​,y3​−y1​,...,yv​−y1​}，所以可以知道，这个平移就是说$Y$中后v-1个向量组成的向量空间按照向量$y_1$的方向进行平移。如果这时有$dimaffY=dim\mathbf{Y}=v-1$，那么仿射包$affY$称为仿射无关（affinely independent）也就是说此时$\mathbf{Y}$中的向量线性无关。否则，仿射包$affY$称为仿射相关，此时$\mathbf{Y}$中的向量线性相关，那么肯定存在$Y$的子集$\bar{Y}$使得$aff\bar{Y}=affY$，因为这个时候$\mathbf{Y}$中最多只要v-2个向量即可满足条件。
然后由线性相关的概念可以知道，式（11）和式（12）中的$l$最大值是这些向量所在的线性空间中的维度再加一，例如二维空间需要三个点才能组成面去覆盖二维的凸包，两个点就只能是线；三维空间需要4个点组成4面体才能覆盖三维的凸包，三个点就只能是面。严格的证明可以查看Caratheodory theorem的证明过程。
定义向量空间$\mathbf{X}$到原点最近的点为$v(\mathbf{X})$，则$v(\mathbf{X})$的长度的计算公式如下：
v ( X ) ∈ X , ∣ v ( X ) ∣ = m i n { ∣ x ∣ : x ∈ X } ( 13 ) v(\bold{X}) \in \bold{X}, |v(\bold{X})| = min\lbrace |x|: x \in \bold{X}\rbrace \kern3em \lparen13\rparen v(X)∈X,∣v(X)∣=min{∣x∣:x∈X}(13)一般来说$v(\mathbf{X})$可能会存在多个点，但是如果X是凸的，那么这个点是唯一的，那么结合式（12）可以得到：
$$v(coX)=\sum _{i=1}^l{\lambda }^i{x}_i,x_i\in X,{\lambda }^i⩾0,{\lambda }^1+...+{\lambda }^l=1(14)$$一般来说，上式中的${\lambda }^i$、$x_i$和$l$都不是唯一的，但是有两点是很重要的，a)如果$v(coX)=0$，那么$l⩽m+1$(m为向量空间的维度)，这是因为原点落在凸包内，结合Caratheodory theorem可以知道结论成立；如果$v(coX)\ne 0$，那么$l⩽m$，因为这个时候原点在凸包之外，那么离原点最近的点一定是落在超平面（凸包的“边”）上。b) { x 1 , x 2 , . . . , x l } \lbrace x_1, x_2, ...,x_l \rbrace {x1​,x2​,...,xl​}仿射无关，这个结论的证明和Caratheodory theorem的相似
定义向量空间$\mathbf{X}$内的函数$h_X(\eta ):R^m\to R$
h X ( η ) = m a x { x ⋅ η : x ∈ X } ( 15 ) h_X(\eta) = max\lbrace x · \eta: x \in \bold{X} \rbrace \kern3em \lparen15\rparen hX​(η)=max{x⋅η:x∈X}(15)这个函数返回获取向量空间内离特定向量最远的点。然后将式（15）改写成：
$$h_X(\eta )=s_X(\eta )\cdot \eta ,s_X(\eta )\in \mathbf{X}(16)$$容易证明$h_X=h_{coX},s_X=s_{coX}$，因为这时候的点一般都是在凸包的顶点上，而这些顶点也必定属于原来的向量空间（凸包的定义），后面有图会体现这点。
对于有限集$Y$，则有：
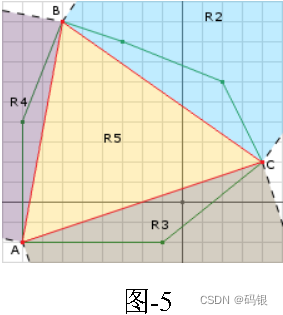
h c o Y = h Y = m a x { y i ⋅ η : i = 1 , 2 , . . . , v } s c o Y = s Y = y j , y j ⋅ η = h Y ( η ) ( 17 ) h_{coY} = h_Y = max\lbrace y_i · \eta: i = 1,2,...,v \rbrace \space s_{coY} = s_Y = y_j, y_j ·\eta = h_Y(\eta)\kern3em \lparen17\rparen hcoY​=hY​=max{yi​⋅η:i=1,2,...,v} scoY​=sY​=yj​,yj​⋅η=hY​(η)(17)上面的概念可以用下面这个图来进行理解：

我认为上面这个图还是比较清晰的，主要是注意各个符号的定义即可。
接下来我们返回公式（4），根据上面提到的概念去求出$d_{ij}$，为了简便，设$i=1,j=2$。根据公式（4）有：
d 12 = m i n { ∣ z ∣ : z ∈ K } = ∣ v ( K ) ∣ , K = K 1 − K 2 ( 18 ) d_{12} = min\lbrace |z|: z \in K \rbrace = |v(K)|, K = K_1 - K_2\kern3em \lparen18\rparen d12​=min{∣z∣:z∈K}=∣v(K)∣,K=K1​−K2​(18)要求$d_{ij}$，首先要求出$h_K$和$s_K$，公式如下：
$$h_K(\eta )=h_{K1}(\eta )+h_{K2}(-\eta ),s_K(\eta )=s_{K1}(\eta )-s_{K2}(-\eta )(21)$$直接这么看有点抽象，用文字描述就是：$h_K(\eta )$等于K1沿着$\eta$方向最长的投影距离减去K2沿着$\eta$方向最短的投影距离，减是因为$h_{K2}(-\eta )$ = $-h_{K2}(\eta )$。通过选取不同的$\eta$可以得到不同的点，如果这些点的凸包包含原点，那么说明K1和K2相交（说明K1和K2存在相同的点）。
现在最关键的问题就是如何有效地选取$\eta$，这一块将在第二部分中解决。