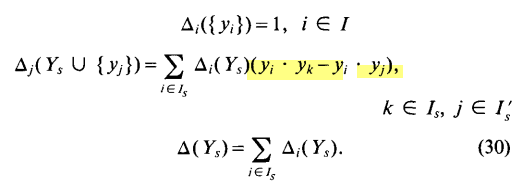原文:dyn4j:GJK (Gilbert–Johnson–Keerthi)
目录
- 1. Minkowski Sum(明可夫斯基和)
- 2. Simplex
- 3. support函数
- 4. 构建Simplex
G J K GJK GJK和 S A T SAT SAT一样用于检测凸多边形,和 S A T SAT SAT不同, G J K GJK GJK可以处理任意形状的凸多边形,然而 S A T SAT SAT处理圆的碰撞检测时需要用不同的算法。
1. Minkowski Sum(明可夫斯基和)
G J K GJK GJK是基于 M i n k o w s k i Minkowski Minkowski S u m Sum Sum概念上的,即形状1的所有点和形状2的所有点之和。
A + B = { a + b ∣ a ∈ A , b ∈ B } A + B = \{a + b | a \in A, b \in B \} A+B={a+b∣a∈A,b∈B}
如果 s h a p e A shape A shapeA和 B B B是凸的,则它们的和也是凸的
相应的可以定义它们的差运算:
A − B = { a − b ∣ a ∈ A , b ∈ B } A - B = \{a - b | a \in A, b \in B \} A−B={a−b∣a∈A,b∈B}
如果两个形状重叠,进行 M i n k o w s k i Minkowski Minkowski S u m Sum Sum后的形状包含原点。 M i n k o w s k i Minkowski Minkowski S u m Sum Sum的运算是 s h a p e shape shape A A A的每个顶点和 s h a p e shape shape B B B的所有顶点求和(或求差)。所得到点的外包络即是运算所得形状。


2. Simplex
单纯形是代数拓扑中的基本概念,单纯形是三角形和四面体的一种泛化,一个 k k k维单纯形是指包含 ( k + 1 ) (k+1) (k+1)个节点的凸多面体。不需要计算 M i n k o w s k i Minkowski Minkowski S u m Sum Sum,只需要计算 M i n k o w s k i Minkowski Minkowski S u m Sum Sum是否包含原点,如果包含原点则两个形状重叠,否则不重叠。在 M i n k o w s k i S u m Minkowski \;\; Sum MinkowskiSum得到的形状中迭代的构建 S i m p l e x Simplex Simplex,判断 S i m p l e x Simplex Simplex是否包含原点,包含则重叠,否则不重叠。
3. support函数
s u p p o r t support support函数返回两个形状 M i n k o w s k i Minkowski Minkowski S u m Sum Sum的一个点用以构建 S i m p l e x Simplex Simplex, s h a p e 1 shape1 shape1的点减去 s h a p e 2 shape2 shape2的点可以得到一个 M i n k o w s k i Minkowski Minkowski S u m Sum Sum的一个点,但我们不希望得到重复的点。使用 s u p p o r t support support函数得到 s h a p e shape shape在一个 d i r e c t i o n direction direction(方向)上的最远点,然后在不同的方向上得到另一个不同的点。在 d i r e c t i o n direction direction上选择最远点可以使生成的 S i m p l e x Simplex Simplex的面积最大化以增加包含原点的几率增加算法收敛速度。使用这种方法得到的点在 M i n k o w s k i Minkowski Minkowski S u m Sum Sum的边上,因此如果得到的点不包含原点则 M i n k o w s k i Minkowski Minkowski S u m Sum Sum不包含原点。
Public Point support(Shape shape1, Shape shape2, Vector d) {// d is a vector direction(doesn't have to normalized)// get points on the edge of the shapes in opposite directionPoint p1 = shape1.getFarthestPointInDirection(d);Point p2 = shape2.getFarthestPointInDirection(d.negative());// perform the Minkowski SumPoint p3 = p1.subtract(p2);// p3 is now a point in Minkowski space on the edge of the Minkowski Differencereturn p3;
}
4. 构建Simplex
首先选择三个点构造 S i m p l e x Simplex Simplex,如果包含原点,则两个多边形重叠,否则重新选择点构建新的 S i m p l e x Simplex Simplex。由 s u p p o r t support support函数可知,需要一个 d i r e c t i o n direction direction来选择 M i n k o w s k i Minkowski Minkowski S u m Sum Sum点,任意的 d i r e c t i o n direction direction都是可以的,但是选择两个多边形的中心点的向量方向是较优的选择。
Vector d = // choose a search direction
// get the first Minkowski Difference point
Simplex.add(support(A, B, d));
// negate d for the next point
d.negate();
// start looping
while (true) {// add a new point to the simplex because we haven't terminated yetSimplex.add(support(A, B, d));// make sure that the last point we added actually passed the originif (Simplex.geLast().dot(d) <= 0) {// if the point added last was not past the origin in the direction of d // then the Minkowski Sum cannot possibly contain the origin since// the last point added is on the edge of Minkowski Differencereturn false;} else {// otherwise we need to determine if the origin is in the current simplexif (Simplex.contains(ORIGIN)) {// if it does then we know there is a collisionreturn true;} else {// otherwise we cannot be certain so find the edge who is closest to the// origin and use its normal (in the direction of the origin) as the new// d and continue the loopd = getDirection(Simplex);}}
}Simplex.geLast().dot(d) <= 0的解释:
S i m p l e x Simplex Simplex最新得到的点是 M i n k o w s k i Minkowski Minkowski S u m Sum Sum在给定方向上的最远点,如果这个点没有 e n c l o s e enclose enclose原点,则 M i n k o w s k i Minkowski Minkowski S u m Sum Sum不会包含原点。如下图, d i r e c t i o n direction direction是 ( − 1 , 0 ) (-1, 0) (−1,0),点 p ( 1 , − 4 ) p(1, -4) p(1,−4)是在 d i r e c t i o n direction direction上的最远点。点 p p p在 d d d上的投影是-1,原点在 d d d上的投影是0,由于 p p p是 M i n k o w s k i Minkowski Minkowski S u m Sum Sum是最远点,所以其不会包含原点。

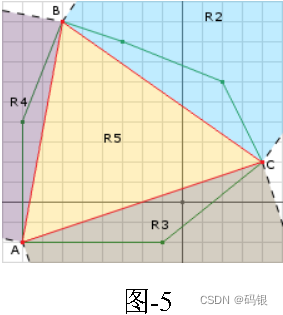
当得到两个 M i n k o w s k i Minkowski Minkowski S u m Sum Sum点时,如下图中左图, B B B是第一个点, A A A是第二个点, A A A和 B B B是 M i n k o w s k i Minkowski Minkowski S u m Sum Sum包络上的点,如果 o r i g i n origin origin在 R 1 R1 R1或者 R 4 R4 R4区域,则 M i n k o w s k i Minkowski Minkowski S u m Sum Sum不包含原点,Simplex.geLast().dot(d) <= 0 返回 t r u e true true。由图可知, o r i g i n origin origin在 R 3 R3 R3区域内,因此需要计算 A B AB AB的 p e r p e t u a l a r perpetualar perpetualar v e c t o r vector vector应该指向 R 3 R3 R3。
A B = B − A A O = O − A p e r p = ( A B × A O ) × A B AB = B - A \\ AO = O - A \\ perp = (AB \times AO) \times AB AB=B−AAO=O−Aperp=(AB×AO)×AB
如右图,此时 s u p p o r t support support函数得到新的 M i n k o w s k i Minkowski Minkowski S u m Sum Sum点 A A A,点 B B B是第二点(左图中的 A A A),点 C C C是第一个点(左图中的 B B B), o r i g i n origin origin可能存在于 R 3 R3 R3、 R 4 R4 R4和 R 5 R5 R5中,计算 ( A C × A B ) × A B (AC \times AB) \times AB (AC×AB)×AB生成 A B p e r p ABperp ABperp,计算 A B p e r p ⋅ ( A O ) ABperp \cdot (AO) ABperp⋅(AO)判断 o r i g i n origin origin是否在 R 4 R4 R4,计算 ( A B × A C ) × A C (AB \times AC) \times AC (AB×AC)×AC生成 A C p e r p ACperp ACperp,计算 A C p e r p ⋅ ( A O ) ACperp \cdot (AO) ACperp⋅(AO)判断 o r i g i n origin origin是否在 R 3 R3 R3。


Vector d = // choose a search direction
// get the first Minkowski Sum point
Simple.add(support(A, B, d));
// nagate d for the next point
d.negate();
// start loop
while (true) {// add a new point to the simplex because we haven't terminated yetSimple.add(support(A, B d));// make sure that the last point added actually passed the originif (Simple.getLast().dot(d) <= 0) {// if the point added last was not past the origin in the direction of d // then the Minkowski Sum cannot possibly contain the origin since// the last point added is on the edge of Minkowski Differencereturn false;} else {// otherwise determine if the origin is in the current simplexif (containsOrigin(Simple, d)) {// if it does, there is a collisionreturn true;}}
}public boolean containOrign(Simples s, Vector d) {// get the last point added to the simplexa = Simplex.getLast(); // the last point// compute AO (same thing as -A)ao = a.negate();if (Simplex.points.size == 3) {// in triangle case// get point B and Cb = Simplex.getB(); // the second pointc = Simplex.getC(); // the first point// compute the edgesab = b - a;ac = c - a;// compute the normalsabPerp = tripleProduct(ac, ab, ab);acPerp = tripltProdect(ab, ac, ac);// is the origin in R4if (adPerp.dot(ao) > 0) {// remove point CSimplex.remove(c);// set the new direction to ABPerpd.set(abPerp);} else {// is the origin in R3if (acPerp.dot(ao) > 0) {// remove point BSimples.remove(b);// set the new direction to ACPerpd.set(acPerp);} else {// otherwise origin in R5, there is a collisionreturn true;}}} else {// in line segment caseb = Simplex.getB();// compute ABab = b -a;// get the perp to AB in the direction of the originabPerp = tripleProduct(ab, ao, ab);// set the direction to ABPerpd.set(abPerp);}return false;
}