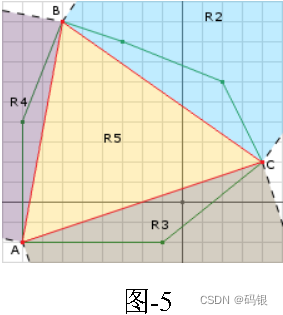
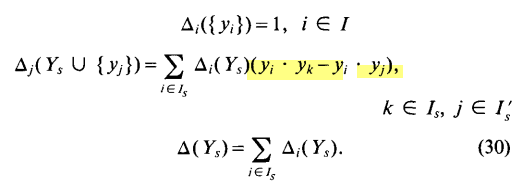引擎开发_ 碰撞检测_GJK 算法详细介绍

概述

和SAT(分离轴定理)算法一样，GJK算法也只对凸体有效。 GJK算法的优势是：通过support函数（后面会详细讲述），从而支持任何凸体形状之间的碰撞检测；相比SAT算法，你不需要一些额外的操作，比如增加特殊的代码和算法处理曲面形状。

GJK是一个迭代算法，但是如果事先给出穿透/分离向量，则它的收敛会很快，可以在常量时间内完成。在3D环境中，GJK可以取代SAT算法。GJK算法的最初目的是计算两个凸体之间的距离，在两个物体穿透深度比较小的情况下，可用它判定物体之间的碰撞。它也可以和别的算法相结合，用来检测两个物体之间深度穿透时候的碰撞情况。

凸体(凸多面体或凸多边形)

面说过，GJK算法只适用于凸体形状。凸体(其实就是一条直线穿越凸体，和该凸体壳的交点不能超过2个)的定义在介绍SAT算法时讲过，可参照那篇文章了解相关信息。

明可夫斯基和(Minkowski Sum)

GJK算法中使用了明可夫斯基和的概念。明可夫斯基和很好理解，假设有两个物体，它们的明可夫斯基和就是物体1上的所有点和物体2上的所有点的和集。用公式表示就是：

A + B = {a + b|a∈A, b∈B}

如果两个物体都是凸体，它们的明可夫斯基和也是凸体。

对于减法，明可夫斯基和的概念也成立，这时也可称作明可夫斯基差。

A – B = A + (-B) = {a + (– b)|a∈A, b∈B} = {a – b)|a∈A, b∈B}

接着往下讲，在两个物体之间执行明可夫斯基差操作的解释如下：

如果两个物体重叠或者相交，它们的明可夫斯基差肯定包括原点。

我们看一个例子，图1中两个物体进行明可夫斯基差操作，将得到图2的形状。可以看到，该形状包含原点，这是因为这两个物体是相交的。

执行这些操作需要物体1的顶点数*物体2的顶点数*2(原作者用的二维向量，如果在三维空间，当然就是*3了，如果是向量减法数量就什么都不用乘了) 个减法操作。物体包含无穷多个点，但由于是凸体，我们可以只对它们的顶点执行明可夫斯基差操作。在执行GJK算法过程中，实际上我们并不需要显式计算物体之间明可夫斯基差，这也是GJK算法的优势所在。

单纯形(Simplex)

我们不需要显式计算物体之间的明可夫斯基差，只要知道它们的明可夫斯基差是否包含原点就ok了。如果包含原点，物体之间就相交，否则，则不相交。

我们可以在明可夫斯基差形成的物体内迭代的形成一个多面体(或多变形），并使这个多面体尽量包围原点。如果这个多面体包含原点，显然明可夫斯基差形成的物体必然包括原点。这个多面体就称作单纯形。

Support函数

下面我们讲述如何建立一个单纯形？首先看什么是support函数，给定两个凸体，该函数返回这两个凸体明可夫斯基差形状中的一个点。我们知道，物体1上的一个点，它的位置减去物体2上的一个点的位置，可以得到它们明可夫斯基差形状上的一个点，但我们不希望每次都得到相同的点。如何保证做到这一点呢？我们可以给support函数传递一个参数，该参数表示一个方向(direction),方向不同，得到的点也不同。

在某个方向上选择最远的点有重要作用，因为这样产生的单纯形包含最大的空间区域，增加了算法快速返回的可能。另外，通过这种方式返回的点都在明可夫斯基差形状的边上。如果我们不能通过一个过原点的方向在单纯形上增加一个点，则明可夫斯基差不过原点，这样在物体不想交的情况下，算法会很快退出。

 public Point support(Shape shape1, Shape shape2, Vector d) {// d is a vector direction (doesn't have to be normalized)// get points on the edge of the shapes in opposite directionsPoint p1 = shape1.getFarthestPointInDirection(d);Point p2 = shape2.getFarthestPointInDirection(d.negative());// perform the Minkowski DifferencePoint p3 = p1.subtract(p2);// p3 is now a point in Minkowski space on the edge of the Minkowski Differencereturn p3;}

下面这个例子使用图2的物体形状，执行函数三次

开始操作，使用d = (1, 0)

p1 = (9, 9);
p2 = (5, 7);
p3 = p1 - p2 = (4, 2);

第二步，使用d = (-1, 0)

p1 = (4, 5);
p2 = (12, 7);
p3 = p1 - p2 = (-8, -2);

注意：p1可能是 (4, 5) 或者 (4, 11)。这两个都将在明可夫斯差形状的边上产生一个点。

下一步假定 d = (0, 1)

p1 = (4, 11);
p2 = (10, 2);
p3 = p1 - p2 = (-6, 9);

这样，我们得到图3所示的单纯形。

判定碰撞

前面我们说过，两个物体的明可夫斯基差中的单纯形包含原点时候，这个两个物体相交。在图3中，单纯形没有包含原点，但实际上，这两个物体是相交的。问题在于我们选择的方向，在第三步中，如果我们选择d = (0, -1) 作为方向，那么

p1 = (4, 5);
p2 = (5, 7);
p3 = p1 - p2 = (-1, -2);

这样产生的单纯形如图4所示，显然它包含了原点，我们由此能够判定这两个物体之间有碰撞。

可见，方向的选择影响输出结果。如果我们得到的单纯形不包含原点的话，我们能够用另一个点代替，产生新的单纯形来判断是否碰撞。这也是这个算法需要迭代的原因。我们不能保证我们最初选择的三个点包含原点，也不能保证明可夫斯基差形状包含原点。

如果我们改变第三个明可夫斯基差图形中选择点的方式，我们就能够包围原点，改变的方式如下所示：

d = ...
a = support(..., d)
d = ...
b = support(..., d)
AB = a - b
AO = a - ORIGIN
d = AB x AO x AB
c = support(..., d)

c 中使用的方向 d 依赖于 a 和 b 形成的直线，通过用相反的方向，我们可以选择离 a 最远的 b 点。

d = ...
a = support(..., d)
b = support(..., -d)
AB = a - b
AO = a - ORIGIN
d = AB x AO x AB
c = support(..., d)

现在，我们仅需要为第一次的明可夫斯基差图形求边界交点选择方向。当然我们也可以选择任意的方向，比如两个物体形状中心的差作为方向等等。怎样选择有很多的优化工作去做。

迭代

即使我们使用上面的方法，也仍有可能在三步内不能得到包含原点的单纯形，所以我们必须用迭代的方法创建单纯形，每次生成的单纯形比上次更接近包含原点。我们也需要检查两个条件：1）现在的单纯形包含原点吗? 2)我们能够包含原点吗?

下面我们看看迭代算法主要代码：

Vector d = // choose a search direction// get the first Minkowski Difference pointSimplex.add(support(A, B, d));//下面开始循环: 第一次迭代
// negate d for the next pointd.negate();// start loopingwhile (true) {// add a new point to the simplex because we haven't terminated yetSimplex.add(support(A, B, d));// make sure that the last point we added actually passed the originif (Simplex.getLast().dot(d) <= 0) {// if the point added last was not past the origin in the direction of d// then the Minkowski Sum cannot possibly contain the origin since// the last point added is on the edge of the Minkowski Differencereturn false;} else {// otherwise we need to determine if the origin is in// the current simplexif (Simplex.contains(ORIGIN)) {// if it does then we know there is a collisionreturn true;} else {// otherwise we cannot be certain so find the edge who is// closest to the origin and use its normal (in the direction// of the origin) as the new d and continue the loopd = getDirection(Simplex);}}
}

下面我们演示一下这个算法框架在图1的例子中如何工作。我们假设最初的方向是2个物体中心的连线的方向。

d = c2 - c1 = (9, 5) - (7.5, 6) = (1.5, -1);
p1 = support(A, B, d) = (9, 9) - (5, 7) = (4, 2);
Simplex.add(p1);
d.negate() = (-1.5, 1);

下面开始循环:
第一次迭代

last = support(A, B, d) = (4, 11) - (10, 2) = (-6, 9);
//we past the origin so check if we contain the origin
// we dont because we are line // get the new direction by (AB x AO) x AB = B(A.dot(C)) - A(B.dot(C))
AB = (-6, 9) - (4, 2)  = (-10, 7);
AO = (0, 0) - (-6, 9) = (6, -9);
ABxAOxAB = AO(149) - AB(-123)= (894, -1341) - (1230, -861)= (-336, -480)= (-0.573, -0.819)

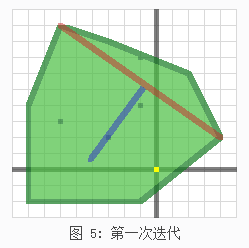
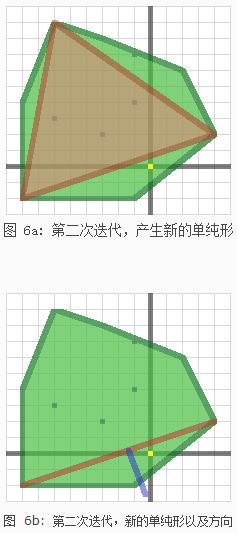
第一次迭代的结果，这时，我们在明可夫斯基差中有一个线段的单纯形（棕色），以及下一次使用的方向（蓝色），这个方向过垂直于上次增加的两个顶点形成的线段(蓝色垂直于棕色)。注意，这个方向不需要归一化，这儿归一化主要是验证给定方向的缩放是否有效。

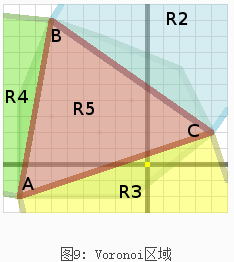
第二次迭代

last = support(A, B, d) = (4, 5) - (12, 7) = (-8, -2)
proj = (-8, -2).dot(-336, -480) = 2688 + 960 = 3648
//we past the origin so check if we contain the origin
//we dont (see Figure 6a)
// the new direction will be the perp of (4, 2) and (-8, -2)
// and the point (-6, 9) can be removed[把离原点较远的点移去]
AB = (-8, -2) - (4, 2)  = (-12, -4);
AO = (0, 0) - (-8, -2) = (8, 2);
ABxAOxAB = AO(160) - AB(-104)= (1280, 320) - (1248, 416)= (32, -96)= (0.316, -0.948)

第二次迭代后，单纯形仍没有包含原点，所以我们不能推断出两个物体是否相交。在第二次迭代中，我们移去了 (-6, 9) 点，因为我们任何时刻只需要 3 个点，我们在迭代开始后，会增加一个新的点。

第三次迭代


last = support(A, B, d) = (4, 5) - (5, 7) = (-1, -2)
proj = (-1, -2).dot(32, -96) = -32 + 192 = 160
// we past the origin so check if we contain the origin
// we do (Figure 7)!

检测单纯形

在上面的算法中，我们通过图和伪代码的形式进行了两个操作：一个是怎么知道现在的单纯形是否包含原点；另一个是我们怎么选择下一次迭代的方向。在前面的伪代码中，为了便于理解，我把这两个步骤分开，但实际上他们应该放在一起，应为它们有很多共用的东西。

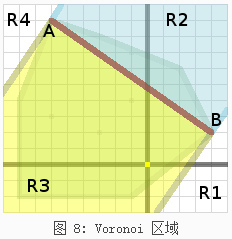
通过一系列基于点积操作的面测试（在二维是线测试），我们能够判定原点位于单纯形的什么位置。首先我们必须处理线段测试，看前面第一次迭代的例子，增加第二个点后(代码第9行)，单纯形现在是一条线段（AB）。我们能够通过Voronoi 区域判定单纯形是否包含原点(看图8).

线段的两个端点是A和B，A是增加到单纯形的最后一个顶点。我们知道A和B在明可夫斯基差的边上，因此原点不能位于R1和R4区域，这是因为11行的代码没有返回false，即AB和AO的点积大于0，所以原点位于R2或者R3区域。当单纯形(这儿是线段)没有包括原点的时候，我们就选择一个新的方向，准备下一次迭代。这可以通过下面的代码完成：

// the perp of AB in the direction of O can be found by
AB = B - A;
AO = O - A;
perp = AB x AO x AB;

当原点位于线段上的时候，我们将得到零向量，在11行的代码将会返回false，如果我们要考虑接触碰撞（两个物体正好接触上），这时就要做一些特殊处理，可以考虑用AB的左手或右手法向作为新的方向。【如果为0，而且原点在AB之间，就可返回true，直接判定为接触碰撞】
第二次迭代中个，我们得到一个三角形单纯形(ABC)（图9）

图中白色的区域不会被测试，因为通过了11行代码的测试[否则会返回false]，显然原点不会位于该区域。R2区域也不可能包含原点，因为上一个方向是在相反的方向，所以我们需要测试的是R3,R4,R5区域，我们能够执行AC x AB x AB 得到一个垂直于AB的向量，接着执行 ABPerp.dot(AO) 去判定是否原点在R4区域（小于0的话不在R4）。

AB = (-6, 9) - (-8, -2) = (2, 11)
AC = (4, 2) - (-8, -2) = (12, 4)
// AC x AB x AB = AB(AC.dot(AB)) - AC(AB.dot(AB))
ABPerp = AB(68) - AC(125)= (136, 748) - (1500, 500)= (-1364, 248)= (-11, 2)
// compute AO
AO = (0, 0) - (-8, -2) = (8, 2)
ABPerp.dot(AO) = -11 * 8 + 2 * 2 = -84
// its negative so the origin does not lie in R4

通过更多的测试，我们能够判定原点的位置:

AB = (-6, 9) - (-8, -2) = (2, 11)
AC = (4, 2) - (-8, -2) = (12, 4)
// AB x AC x AC = AC(AB.dot(AC)) - AB(AC.dot(AC))
ACPerp = AC(68) - AB(160)= (816, 272) - (320, 1760)= (496, -1488)= (1, -3)
// compute AO
AO = (0, 0) - (-8, -2) = (8, 2)
ACPerp.dot(AO) = 1 * 8 + -3 * 2 = 2
// its positive so that means the origin lies in R3正值表示在R3,负的表示在R5

所以我们能够判定原点在R3区域。最后，我们还要选择一个方向，以便得到在此方向上的下一个明可夫斯基点。由于已经知道AC的Voronoi区域包含原点，所以这是很容易实现的：
AC x AO x AC
这时，已经不需要点B,所以我们去掉它。最终代码如下所示：

Vector d = // choose a search direction// get the first Minkowski Difference pointSimplex.add(support(A, B, d));// negate d for the next pointd.negate();// start loopingwhile (true) {// add a new point to the simplex because we haven't terminated yetSimplex.add(support(A, B, d));// make sure that the last point we added actually passed the originif (Simplex.getLast().dot(d) <= 0) {// if the point added last was not past the origin in the direction of d// then the Minkowski Sum cannot possibly contain the origin since// the last point added is on the edge of the Minkowski Differencereturn false;} else {// otherwise we need to determine if the origin is in// the current simplexif (containsOrigin(Simplex, d) {// if it does then we know there is a collisionreturn true;}}}public boolean containsOrigin(Simplex s, Vector d) {// get the last point added to the simplexa = Simplex.getLast();// compute AO (same thing as -A)ao = a.negate();if (Simplex.points.size() == 3) {// then its the triangle case// get b and cb = Simplex.getB();c = Simplex.getC();// compute the edgesab = b - a;ac = c - a;// compute the normalsabPerp = tripleProduct(ac, ab, ab);acPerp = tripleProduct(ab, ac, ac);// is the origin in R4if (abPerp.dot(ao) > 0) {// remove point cSimplex.remove(c);// set the new direction to abPerpd.set(abPerp);} else {// is the origin in R3if (acPerp.dot(ao) > 0) {// remove point bSimplex.remove(b);// set the new direction to acPerpd.set(acPerp);} else{// otherwise we know its in R5 so we can return truereturn true;}}} else {// then its the line segment caseb = Simplex.getB();// compute ABab = b - a;// get the perp to AB in the direction of the originabPerp = tripleProduct(ab, ao, ab);// set the direction to abPerpd.set(abPerp);}return false;}

上面是二维凸多边形碰撞检测的代码。在判断原点是否包含在多面体中(两个物体的明可夫斯基差）时，我们使用了在基于三角形的单纯形测试法。这是根据Caratheodory定理：一个凸多面体的中任意一个点，能够被表示为其n+1点的组合。凸多面体是2维的，所以测试时用了三角形(3个点)，在3D的情况下，我们则需要测试四面体就ok了(4个点)。
现在已经完成了GJK碰撞检测算法教程。最初的GJK算法是计算两个凸体之间的距离。另外，如果你需要碰撞信息，比如法向和深度，你应该自己修改GJK算法或者把它和别的算法结合起来。EPA就是一个这样的算法。