这里要先纠正上篇文章的一些错误，就是上篇文章的最后其实并没有证明定理3，而只是给出了仿射集系数向量 $\lambda$的解的形式，而没有进一步说明如何从定理3的各个条件推导出结论；然后是之前把余子式和代数余子式的概念混杂在一起了，所以文中有些描述也错了。对于以上两点疏忽，我向大家道个歉。我修改了上篇文章的一些描述，整体内容没有变化，所以这篇文章继续从附录二开始，然后讲完第五部分。
为防止混乱，我这里先说明一下，文章内有时候会用 $y_i$表示点，有时候又会用 $x_i$表示点，但无论如何，只要是同一类型的符号就代表是在同一个集合内的，关键是抓住定义，所以不用纠结用的是哪一个符号。

再探Appendix Ⅱ

内容详解

在上一篇文章的最后，我们得到了仿射集系数${\lambda }^i$的形式，即下式：
$${\lambda }^i={\Delta }_i(Y_S)/\Delta (Y_S)$$然后进入引理1的分析。
引理1：当且仅当$Y_S$是仿射独立时，行列式$\Delta (Y_S)>0$。要证明这条引理，首先需要回顾(40)式和(41)式：

然后将$A_S$第一列除第一个元素外都变成0，也就是论文里提到的第二行之后每一行加上$(x_1-x_i)\cdot x_1$（看到$(x_1-x_i)\cdot x_1$和第一列的元素有什么区别吗？就是差一个负号）。这样的话$A_S$就会变成下面的矩阵：
$$\begin{gathered} \left|\begin{array}{cccc}1& 1& ...& 1\\ 0& (x_2-x_1)\cdot x_2-(x_2-x_1)\cdot x_1& ...& (x_2-x_1)\cdot x_r-(x_2-x_1)\cdot x_1\\ ...& ...& ...& ...\\ 0& (x_r-x_1)\cdot x_2-(x_r-x_1)\cdot x_1& ...& (x_r-x_1)\cdot x_r-(x_r-x_1)\cdot x_1\end{array}\right|= \\ \left|\begin{array}{cccc}1& 1& ...& 1\\ 0& (x_2-x_1)\cdot (x_2-x_1)& ...& (x_2-x_1)\cdot (x_r-x_1)\\ ...& ...& ...& ...\\ 0& (x_r-x_1)\cdot (x_2-x_1)& ...& (x_r-x_1)\cdot (x_r-x_1)\end{array}\right| \end{gathered}$$等式的右边是不是很有规律？它可以变成$Q_S^T{Q}_S$，其中$Q_S$是矩阵：

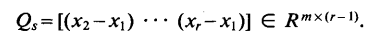
这里要注意，$x_i$是列主序的向量，所以$Q_S$确实是一个矩阵。当然你可以把$x_i$都拆开再进行矩阵的乘法，不过得到的是一样的结果。根据行列式的计算公式有：$det(A_S)=det(Q_S^T{Q}_S)$，所以$det(A_S)⩾0$，并且矩阵$rank(A_S)=rank(Q_S)$（rank代表矩阵的秩），如果$det(A_S)>0$那么代表$rank(A_S)=rank(Q_S)=r-1$，又因为矩阵$A_S$内的元素是集合$Y_S$内的点的线性组合，那么必然有$dimY=r-1$。回到第一篇文章，我们可以知道，如果$dimaffY=dimY=r-1$，那么说明$Y_S$是仿射独立的。至此，引理1证明完毕。
之前提到(30)式有很多新出现的符号，我们还未了解，所以不讲。但是现在我们已经有足够的知识去理解了，而且接下来的内容也需要用到(30)式，所以接下来先返回到第五部分的(30)式，梳理完之后会回到第五部分，这里主要是接着上面的思路，所以没有把(30)式的分析放到第五部分。
(30)式内容如下：

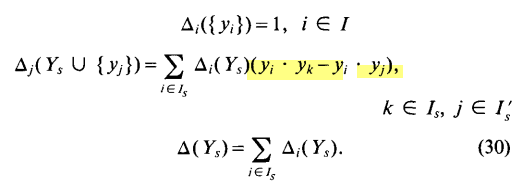
这里面有三个式子，这里分别称为30.1、30.2以及30.3。(30.1)式我自己是觉得有点疑惑的，与其说是公式，不如说是补充定义，因为只有一个点的话计算这个值也没有什么意义。(30.3)式应该比较好理解，这个就是使用代数余子式计算行列式的公式。关键是(30.2)式，简单来说就是按照(41)式的规律，往$A_S$矩阵加入$y_j$向量后，再取第一行$y_j$那列的代数余子式，这里以2阶的$A_S$矩阵为例
$$A_S=\left|\begin{array}{cc}1& 1\\ (y_2-y_1)\cdot y_1& (y_2-y_1)\cdot y_2\end{array}\right|$$那么加入$y_j$后的矩阵$A_S^j$则为：
$$A_S^j=\left|\begin{array}{ccc}1& 1& 1\\ (y_2-y_1)\cdot y_1& (y_2-y_1)\cdot y_2& (y_2-y_1)\cdot y_j\\ (y_j-y_1)\cdot y_1& (y_j-y_1)\cdot y_2& (y_j-y_1)\cdot y_j\end{array}\right|$$
然后根据上一篇文章的内容，可以知道：
Δ j ( Y S ⋃ { y j } ) = ( − 1 ) ( 1 + 3 ) d e t ∣ ( y 2 − y 1 ) ⋅ y 1 ( y 2 − y 1 ) ⋅ y 2 ( y j − y 1 ) ⋅ y 1 ( y j − y 1 ) ⋅ y 2 ∣ \Delta_j(Y_S \bigcup \lbrace y_j \rbrace) = (-1)^{(1 + 3)}det\begin{vmatrix} (y_2 - y_1)·y_1 & (y_2 - y_1)·y_2 \\ (y_j - y_1)·y_1 & (y_j - y_1)·y_2 \\ \end{vmatrix} Δj​(YS​⋃{yj​})=(−1)(1+3)det∣∣∣∣​(y2​−y1​)⋅y1​(yj​−y1​)⋅y1​​(y2​−y1​)⋅y2​(yj​−y1​)⋅y2​​∣∣∣∣​如果取最后一行的代数余子式来进行行列式计算，那么：
Δ j ( Y S ⋃ { y j } ) = ( − 1 ) ( 1 + 3 ) ∗ ( − 1 ) ( 1 + 2 ) ( ( y j − y 1 ) ⋅ y 1 ) ( ( y 2 − y 1 ) ⋅ y 2 ) + ( − 1 ) ( 1 + 3 ) ∗ ( − 1 ) ( 1 + 3 ) ( ( y j − y 1 ) ⋅ y 2 ) ( ( y 2 − y 1 ) ⋅ y 1 ) ( a ) \Delta_j(Y_S \bigcup \lbrace y_j \rbrace) = (-1)^{(1 + 3)}* (-1)^{(1 + 2)}((y_j - y_1)·y_1)((y_2 - y_1)·y_2) + (-1)^{(1 + 3)}* (-1)^{(1 + 3)}((y_j - y_1)·y_2)((y_2 - y_1)·y_1) \kern3em \lparen a \rparen Δj​(YS​⋃{yj​})=(−1)(1+3)∗(−1)(1+2)((yj​−y1​)⋅y1​)((y2​−y1​)⋅y2​)+(−1)(1+3)∗(−1)(1+3)((yj​−y1​)⋅y2​)((y2​−y1​)⋅y1​)(a)然后我们仔细分析一下上面这个式子，有没有发现，其实$${\Delta }_1{Y}_S=(-1{)}^{(1+1)}((y_2-y_1)\cdot y_2)$$而$${\Delta }_2{Y}_S=(-1{)}^{(1+2)}((y_2-y_1)\cdot y_1)$$
那么(a)式可以写成：
Δ j ( Y S ⋃ { y j } ) = − 1 ∗ Δ 1 Y S ( ( y j − y 1 ) ⋅ y 1 ) + ( − 1 ) ∗ Δ 2 Y S ( ( y j − y 1 ) ⋅ y 2 ) \Delta_j(Y_S \bigcup \lbrace y_j \rbrace) = -1*\Delta_1Y_S((y_j - y_1)·y_1) + (-1)*\Delta_2Y_S((y_j - y_1)·y_2) Δj​(YS​⋃{yj​})=−1∗Δ1​YS​((yj​−y1​)⋅y1​)+(−1)∗Δ2​YS​((yj​−y1​)⋅y2​)这个就是(30.2)式！理解(30.2)式非常重要，因为这是证明定理3的一个关键。想要进一步熟悉的不妨推导一下4阶的$A_S$矩阵。

再探The Distance Subalgorithm

内容详解

有了上面几篇文章的基础，现在我们终于能去证明定理3了，这真的是一个漫长的过程，但也代表我们快要看到曙光了。这一部分虽然是在说第五部分，但是实际上证明的主题还是在附录二上，这样安排是为了思路能够更加连贯（我自己也不想每隔几行就插个标题，然后跳来跳去）。首先我们来看一下定理3的描述。
定理3：当且仅当
\kern3em 1）$\Delta (Y_S)>0$；
\kern3em 2）$\forall i\in I_S,{\Delta }_i(Y_S)>0$；
\kern3em 3） ∀ i ∈ I S ′ , Δ j ( Y S ⋃ { y j } ) ⩽ 0 \forall i \in I_S',\Delta_j(Y_S \bigcup \lbrace y_j \rbrace) \leqslant 0 ∀i∈IS′​,Δj​(YS​⋃{yj​})⩽0
时，集合$Y$的凸包离原点最近的点能够以(29)式的形式进行表示。这里要注意的是$I_S^{\prime }$表示的是$I_S$的补集，也就是说如果 Y = { y 1 , y 2 , y 5 , y 6 } Y = \lbrace y_1, y_2, y_5, y_6\rbrace Y={y1​,y2​,y5​,y6​}，那么 I = { 1 , 2 , 5 , 6 } I = \lbrace 1, 2, 5, 6\rbrace I={1,2,5,6}，然后 Y S = { y 1 , y 5 , y 6 } Y_S = \lbrace y_1, y_5, y_6\rbrace YS​={y1​,y5​,y6​}，那么 I S = { 1 , 2 , 6 } I_S = \lbrace 1, 2, 6\rbrace IS​={1,2,6}， I S ′ = { 5 } I_S' = \lbrace 5 \rbrace IS′​={5}。下面是证明过程。

过程1

首先是根据(41)式，当且仅当下面式子成立:
$$y\cdot (y-y_k)=0\forall k\in I_S(43)$$才有$y=v(aff{Y}_S)$。这怎么得到的？我们回到(41)式，然后用$A_S$矩阵的第二行去和$\lambda$向量相乘，得到：
$${\lambda }^1(x_2-x_1)\cdot x_1+{\lambda }^2(x_2-x_1)\cdot x_2+...+{\lambda }^r(x_2-x_1)\cdot x_r=0$$合并一下多项式，得到：
$$({\lambda }^1{x}_1+{\lambda }^2{x}_2+...+{\lambda }^r{x}_r)\cdot (x_2-x_1)$$根据(12)式，以及$y$的定义，能得到：
$y\cdot (x_2-x_1)=0(1)$
同样的，我们能够得到以下式子：
$y\cdot (x_3-x_1)=0(2)$
$...$
$y\cdot (x_r-x_1)=0(r-1)$
然后将这r个式子乘以对应的系数${\lambda }^{i+1}$再相加，我们能得到：
$$y\cdot ({\lambda }^2{x}_2+...{\lambda }^r{x}_r-({\lambda }^2+...{\lambda }^r)x_1)=0$$然后${\lambda }^2{x}_2+...{\lambda }^r{x}_r=y-{\lambda }^1{x}_1$，$({\lambda }^2+...{\lambda }^r)=1-{\lambda }^1$，综合这些式子就能得到(43)式，从而也说明了$y=v(aff{Y}_S)$。

过程2

设$y=v(aff{Y}_S)$，并且假定定理3的1)和2)都满足，那么从引理1以及(42)式出发，我们可以用(29)式和(31)式来表示$y$，具体原因其实在文章叙述的过程中已经讲解了，这里就不再阐述。

过程3

定理3的条件1)和3)、(42)式加上(30)式表明$y\cdot (y_k-y_j)⩽0$，这个代入公式应该也不难理解，所以这里也不再阐述。
综合过程1、2、3，我们能得到以下信息：对于$\forall x\in coY$，我们有：
$$x=\sum _{i=1}^v{\alpha }^i{y}_i,\sum _{i=1}^v{\alpha }^i=1,{\alpha }^i⩾0$$这里的点的符号又变了，但不需要太纠结，抓住$\forall x\in coY$就好，上面的式子就是(12)式。那么我们可以得到下面的式子：
$$y\cdot (y-x)=\sum _{i=1}^v{\alpha }^{i}y\cdot (y-y_i)⩽0$$然后我们根据(43)式可以知道上面的式子等于0，那么这代表了$g_{coY}(y)=0$，$g_K(x)$的定义请参照(25)式，从而说明y就是离原点最近的点，即$v(coY)=y$。
可能大家会有点晕，最后我梳理一下，简单来说就是使用定理3来找距离原点最近的点，就是上面提到的$y$，只要满足定理3，那么这个点就是我们要找的点。
那么，我们终于可以写出这个子算法的过程了：
Distance Subalgorithm：对有限集 Y = { y 1 , . . . , y v } ⊂ R m Y = \lbrace y_1,...,y_v \rbrace \subset R^m Y={y1​,...,yv​}⊂Rm，按一定的索引集构造集合$Y_s$，其中$s=1,2,...,\sigma$，$\sigma$的定义为：
$$\sigma =\sum _{k=1}^v[v!/(k!(v-k)!)]$$（这里要注意的是$s$是一个数字，结合$\sigma$的定义可知，在有4个点的情况下，我们可以设定$s=1$时， Y s = { y 1 } Y_s=\lbrace y_1\rbrace Ys​={y1​}；$s=2$时， Y s = { y 2 } Y_s=\lbrace y_2\rbrace Ys​={y2​}；$s=15$时， Y s = { y 1 , y 2 , y 3 , y 4 } Y_s=\lbrace y_1, y_2, y_3, y_4\rbrace Ys​={y1​,y2​,y3​,y4​}），然后按照下面的步骤进行处理：
\kern3em 1.s = 1;
\kern3em 2.如果$Y_s$中的顶点满足定理3的所有条件，那么使用(29)式以及(31)式对$v(coY)$进行表示并且返回结果；
\kern3em 3.如果$s<\sigma$，那么s = s + 1，然后返回到步骤1继续执行；
\kern3em 4.如果上述步骤都没有得到结果，说明算法出了问题，返回错误。

到此，GJK的主要内容已经阐述得差不多了，后面我会把第六部分也梳理出来，第六部分主要是让整个算法更加健壮。然后我会加上一个简单的例子，让大家能更好的理解。