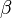Essence本质:LDA模型主要包括主题分布θ和词语分布,
- 主题分布:各个主题在文档中出现的概率分布。
- 词语分布:各个词语在某个主题下出现的概率分布。
pLSA模型中这两个分布是固定的,由期望最大化EM(Expectation Maximization)算法求参;
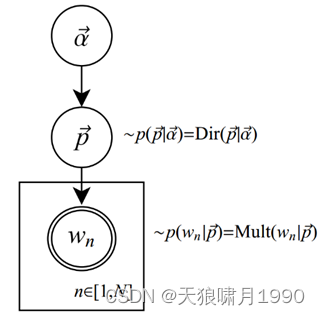
而LDA模型中这两个分布是随机的,由Dirichlet分布生成,而Dirichlet分布的参数α和β由Gibbs采样生成。
目录
1. 简介
1.1 LDA overall framework
1.2 Concept
1.3 对比:词袋模型和LDA模型
1.4 LDA模型生成文档过程
2. LDA基础知识
2.1 Gamma函数
2.2 伯努利分布
2.3 二项分布Binomial Distribution
2.4 多项分布Multinomial Distribution
2.5 Beta分布,二项分布的共轭先验分布
2.6 Dirichlet分布,多项分布的共轭先验分布
2.7 先验分布与后验分布
3. LDA主题模型
3.1 频率派与贝叶斯派
3.2 LDA基础模型
3.2.1 Unigram model一元模型
3.2.2 Mixture of unigrams model
3.3 pLSA模型(Probabilistic latent semantic analysis)
3.3.1 steps: pLSA得到"文档-词项"生成模型的步骤
3.3.2 example: pLSA模型生成文档
3.3.3 Problem: 词袋模型,未关注词与词之间的顺序
3.3.4 Understanding: pLSA模型
3.3.5 根据文档反推其主题分布
3.3.6 EM算法
3.3.6.1 E-step
3.3.6.2 M-step
3.4 LDA模型生成文档过程
3.5 pLSA与LDA区别
3.6 Gibbs采样
4. LDA codes
4.1 LDA implementation 1
4.2 LDA implementation 2
4.3 Ida2vec implementation
1. 简介
1.1 LDA overall framework
(1) 一个函数:gamma函数
(2) 四个分布:二项分布、多项分布、beta分布、Dirichlet分布
(3) 一个概念和一个理念:共轭先验、贝叶斯框架
(4) 两个模型:pLSA和LDA
(5) 一个采样:Gibbs采样
1.2 Concept
LDA(Latent Dirichlet Allocation)主题模型,它可以将文档集中每篇文档的主题以概率分布的形式给出。
1.3 对比:词袋模型和LDA模型
词袋模型:推测一篇文章是如何生成的
以一定的概率选取某个主题,再以一定的概率选取那个主题下的某个单词,不断重复这两步,最终生成一篇文档。(其中不同颜色的词语分别对应上图中不同主题)


LDA模型:根据给定的training文档,反推其主题分布。
各篇文章分别都写了些啥主题,且各篇文章中各个主题出现的概率大小(主题分布)是啥
1.4 LDA模型生成文档过程
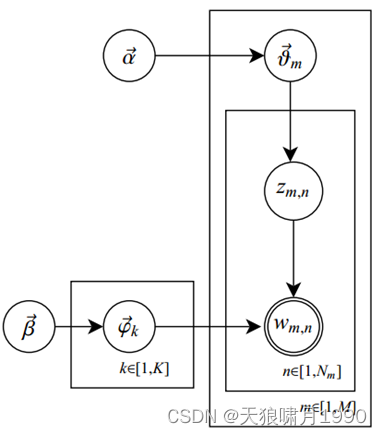
在LDA topic model中,文档生成方式如下:
1) 从Dirichlet分布α中取样生成文档i的主题分布θi;
2) 从主题多项分布θi中取样生成文档第j个词的主题Zi,j
3) 根据主题Zi,j,从Dirichlet分布β中取样生成主题Zi,j对应的词语分布
4) 从词语多项分布 中采样最终生成词语Wi,j
其中,Beta分布是二项分布的共轭先验概率分布,而Dirichlet分布是多项式分布的共轭先验概率分布。
2. LDA基础知识
2.1 Gamma函数
2.2 伯努利分布
伯努利分布就是最简单的0-1分布,搞科学的这群人就喜欢炒概念!!!
p(x=0)=p; p(x=1)=1-p
2.3 二项分布Binomial Distribution
2.4 多项分布Multinomial Distribution
二维分布扩展到多维的情况
2.5 Beta分布,二项分布的共轭先验分布
给定参数α>0和β>0,取值范围为[0,1]的随机变量x的概率密度函数:
其中,,
是gamma函数
2.6 Dirichlet分布,多项分布的共轭先验分布
Dirichlet分布是Beta分布在高维上的推广
2.7 先验分布与后验分布
- 先验分布:即根据已有数组的概率分布,推测未发生事件的概率。e.g. 已有天气数据,推测明天是否下雨。
- 后验分布:即根据预测事件发生概率,分析已有数据的概率分布。e.g. 已经天气预报数据因为涂鸦丢失而损坏了一部分,只能得到部分概率分布,这时根据明天下雨事件的概率,推测已有天气数据的概率分布。
3. LDA主题模型
3.1 频率派与贝叶斯派
- 频率派:把需要推断的参数θ看作是固定的未知数。即概率θ是未知的,但最起码是确定的一个值,同时,样本x是随机的,所以频率派重点研究样本空间,大部分的概率计算都是针对样本x的分布。
- 贝叶斯派:待估计的参数θ是随机的,服从一定的分布,而样本x是固定的,由于样本是固定的,所以他们重点研究的是参数θ的分布。
3.2 LDA基础模型
w, 表示词语。V表示所有单词的个数(固定值)
z, 表示主题。K是主题的个数(预先设定的固定值)
D=(d1,d2,...,dm)表示语料库。其中m是语料库中的文档数
d=(w1,w2,...,wn)表示文档。其中n表示一篇文档中单词数(随机变量)
3.2.1 Unigram model一元模型
Unigram model假设文本中的词服从Multinomial分布
对于文档d=(w1,w2,...,wn),用p(wn)表示词wn的先验概率,生成文档d的概率:
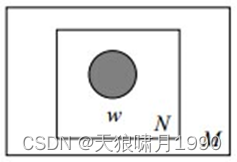
p是词服从Multinomial分布的参数
α是Dirichlet分布(即Multinomial分布的先验分布)的参数
3.2.2 Mixture of unigrams model
该模型的生成过程:给某个文档选择一个主题z,再根据该主题生成文档,该文档中的所有词都来自一个主题。假设主题有z1,z2,...,zk,生成文档d的概率为:
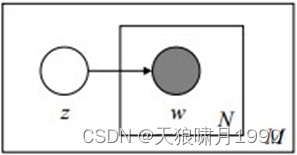
3.3 pLSA模型(Probabilistic latent semantic analysis)
3.3.1 steps: pLSA得到"文档-词项"生成模型的步骤
p(di})--表示海量文档中某篇文档被选中的概率
p(wj|di)--表示词wj在给定文档di中出现的概率
p(zk|di)--表示某个主题zk在给定文档di下出现的概率
p(wj|zk)--表示具体某个词wj在给定主题zk下出现的概率,与主题关系越密切的词,其条件概率p(wj|zk)越大。
(1) 按照概率p(di)选择一篇文档di
(2) 选定文档di后,从主题分布中按照概率p(zk|di)选择一个隐含的主题类别zk
(3)选定zk后,从词语分布中按照概率p(wj|zk)选择一个词wj。
3.3.2 example: pLSA模型生成文档
requirement: 你要写M篇文档,每篇文档由不同的词组成。
condition: 由K个可供选择的主题,由V个可选的词。
(1)每写一篇文档,就制作一颗K面的"文档-主题"骰子,和K个V面的"主题-词项"骰子。比如:令K=3,V=3,得到

(2) 每写一个词,先扔该"文档-主题"骰子选择主题,得到主题结果后,使用和主题对应的那颗"主题-词项"骰子,扔该骰子选择要写的词。
主题分布:各个主题在文档d中出现的概率分布,比如{教育:0.5,经济:0.3,交通:0.2},这是一个多项分布multi-nomial。
同理,词项分布也是一个多项分布。先从主题分布{教育:0.5,经济:0.3,交通:0.2}中抽取出主题:教育,然后从该教育主题对应的词分布{大学:0.5,老师:0.3,课程:0.2}中抽取出词:大学。
(3) 最后,重复扔"文档-主题"骰子和"主题-词项"骰子,重复N次(产生N个词),完成一篇文档,重复这产生一篇文档的方法M词,就完成M篇文档。
3.3.3 Problem: 词袋模型,未关注词与词之间的顺序
3.3.4 Understanding: pLSA模型
pLSA模型假设一组共现(co-occurrence)词项关联着一个隐含的主题类别zk∈{z1,z2,...,zk}。即假定某个主题zk下单词wi容易和某个单词wj共同作用,形成共现,e.g. 小米加步枪。
3.3.5 根据文档反推其主题分布
这是主题建模的目的:自动地发现文档training set中的主题分布。
由于p(di)和p(wj|di)可以事先算出,用EM算法估计pLSA模型的两个位置参数p(wj|zk)和p(zk|di)。
3.3.6 EM算法
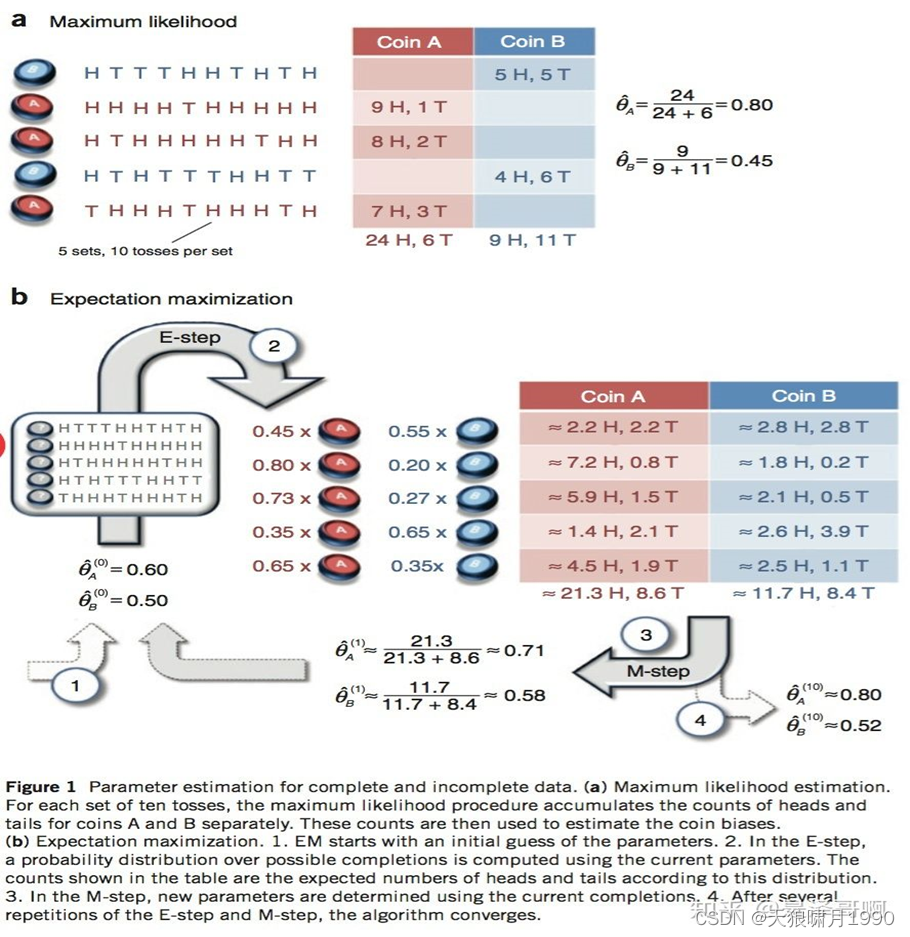
Essence本质:先随机设置初始概率,然后通过期望求出贡献,用极大似然估计新的概率,最终在反复迭代后,概率值极大逼近真实概率。
EM算法的思想非常简单,分为两步:Expection-Step和Maximization-Step。
- E-step主要通过观察数据和现有模型来估计参数,然后用这个估计的参数值来计算似然函数的期望。
- M-step是寻找似然函数最大化时对应的参数。
由于EM算法保证在每次迭代之后似然函数都会增加,所以函数最终会收敛。
Example:假设有两枚硬币A和B,它们的随机抛掷结果如下如所示:
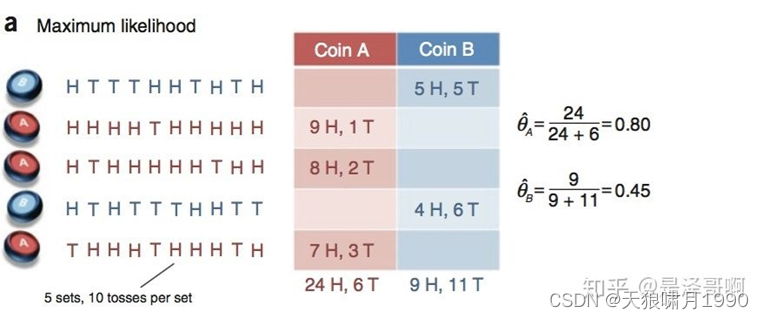
我们很容易估计出两枚硬币抛出正面的概率:
θA=0.8;θB=0.45
现在我们加入隐变量,抹去每轮投掷的硬币标记:
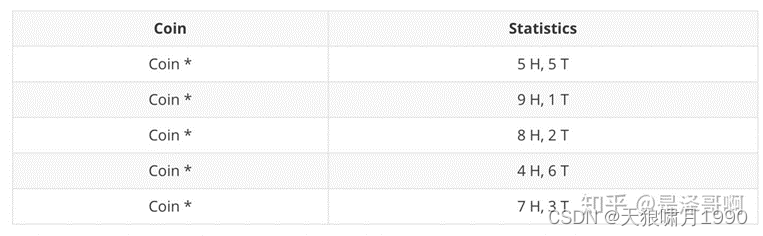
碰到这种情况,我们该如何估计θA和θB的值?
我们多了一个隐变量Z=(z1,z2,z3,z4,z5),代表每一轮所使用的硬币,我们需要知道每一轮抛掷所使用的硬币这样才能估计θA和θB的值,但估计隐变量Z我们又需要知道θA和θB的值,才能用极大似然估计法去估计出Z。这样就陷入了一个鸡生蛋还是蛋生鸡的问题。
Solution:其解决办法就是先随机初始化θA和θB,然后用去估计Z,然后基于Z按照最大似然概率去估计新的θA和θB,循环至收敛。
随机初始化θA=0.6,θB=0.5。
对于第一轮来说,如果是硬币A,得出5正5反的概率为 ;如果是硬币B,得到 5 正 5 反的概率为:
。我们可以算出使用硬币A和使用硬币B的概率分别为:

3.3.6.1 E-step
从期望的角度来看,对于第一轮抛掷,使用硬币A的概率是0.45,使用硬币B的概率是0.55。同理其他轮。这一步我们实际上是估计出了Z的概率分布,这就是E-step。
结合硬币A的概率和上一张投掷结果,我们利用期望可以求出硬币A和硬币B的贡献。
H: 0.8*9=7.2
T: 0.8*1=0.8

3.3.6.2 M-step
然后用极大似然估计来估计新的θA 和θB。
这步就对应了M-step,重新估计出了参数值。
如此反复迭代,我们就可以算出最终的参数值。
3.4 LDA模型生成文档过程
LDA就是在pLSA基础上加层贝叶斯框架,文档生成过程如下:
(1) 按照先验概率p(di)选择一篇文档。
(2) 从Dirichlet分布α中取样生成文档di的主题分布θi,即主题分布θi是由超参数α的Dirichlet分布生成的。
(3)从主题的多项式分布θi中取样生成文档di第j个词的主题Zi,j
(4) 从Dirichlet分布β中取样生成主题Zi,j对应的词语分布
(5) 从词语的多项式分布中采样最终生成词语Wi,j。
3.5 pLSA与LDA区别
(1) 生成文档过程不同
在pLSA中,主题分布和词分布是唯一确定的。{教育:0.5,交通:0.3}
在LDA中,主题分布和词分布不再是唯一确定的,而是由Dirichlet先验随机确定。可能是{教育:0.5,交通:0.3},也可能是{教育:0.4,交通:0.4}
(2) 反推 -> 估计未知参数的方式不同
pLSA模型:EM算法
LDA:Gibbs采样
3.6 Gibbs采样
Essence本质:以条件概率 -> 模拟联合概率分布
- 条件:需要知道条件概率
- 思想:Gibbs采样是Markov Chain Monte Carlo(MCMC)的一种算法,MCMC借助Markov链的平稳分布特征模拟高维概率分布!
Gibbs采样是通过条件分布采样模拟联合分布,再通过模拟的联合分布直接推导出条件分布,以此循环。当Markov链经过burn-in阶段,消除初始参数的影响,到达平稳状态后,每一次状态转移都可以生成待模拟分布的一个样本。
e.g. 跳过初始的一定数量的单元(比如100个),然后隔一定的数量取一个单元(比如隔20个取一个),这样sample的单元是逼近联合分布的。
- 意义:多维/高维(2维以上)积分、期望或联合分布是很难计算的,这时才需要Gibbs采样,得到近似解!
- 例子:
甲只能;E:吃饭、学习、打球,
时间;T:上午、下午、晚上,
天气;W:晴朗、刮风、下雨。
现在要一个sample,这个sample可以是:打球+下午+晴朗。
Condition:p(E|T,W),p(T|E,W),p(W|E,T)。现在要做的就是通过这三个已知的条件分布,再用gibbs sampling的方法,得到联合分布。
首先随便初始化一个组合,i.e. 学习+晚上+刮风,
然后依条件概率改变其中的一个变量。
具体说,假设我们知道晚上+刮风,我们给E生成一个变量,比如,学习-》吃饭。我们再依条件概率改下一个变量,根据学习+刮风,把晚上变成上午。类似地,把刮风变成刮风(当然可以变成相同的变量)。这样学习+晚上+刮风->吃饭+上午+刮风。
同样的方法,得到一个序列,每个单元包含三个变量,也就是一个马尔可夫链。然后跳过初始的一定数量的单元(比如100个),然后隔一定的数量取一个单元(比如隔20个取1个)。这样sample到的单元,是逼近联合分布的。
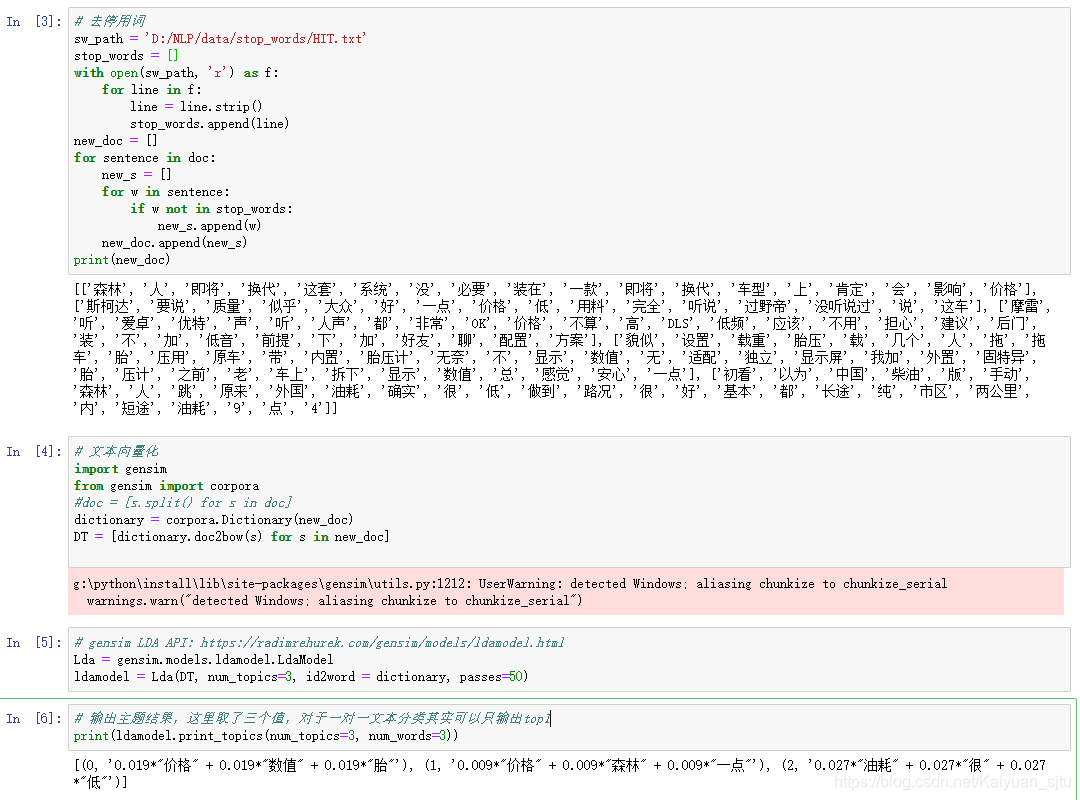
4. LDA codes
4.1 LDA implementation 1
github address: topic_models/LDA-demo at master · laserwave/topic_models · GitHub
python-codes package编解码包
codes.encode(obj, encoding='utf-8', errors='strict'),使用encoding指定的编解码器对obj进行编码,类似str.encode()方法
codes.decode(obj, encoding='utf-8', errors='strict'),使用encoding指定的编解码器对obj进行解码,类似str.decode()方法
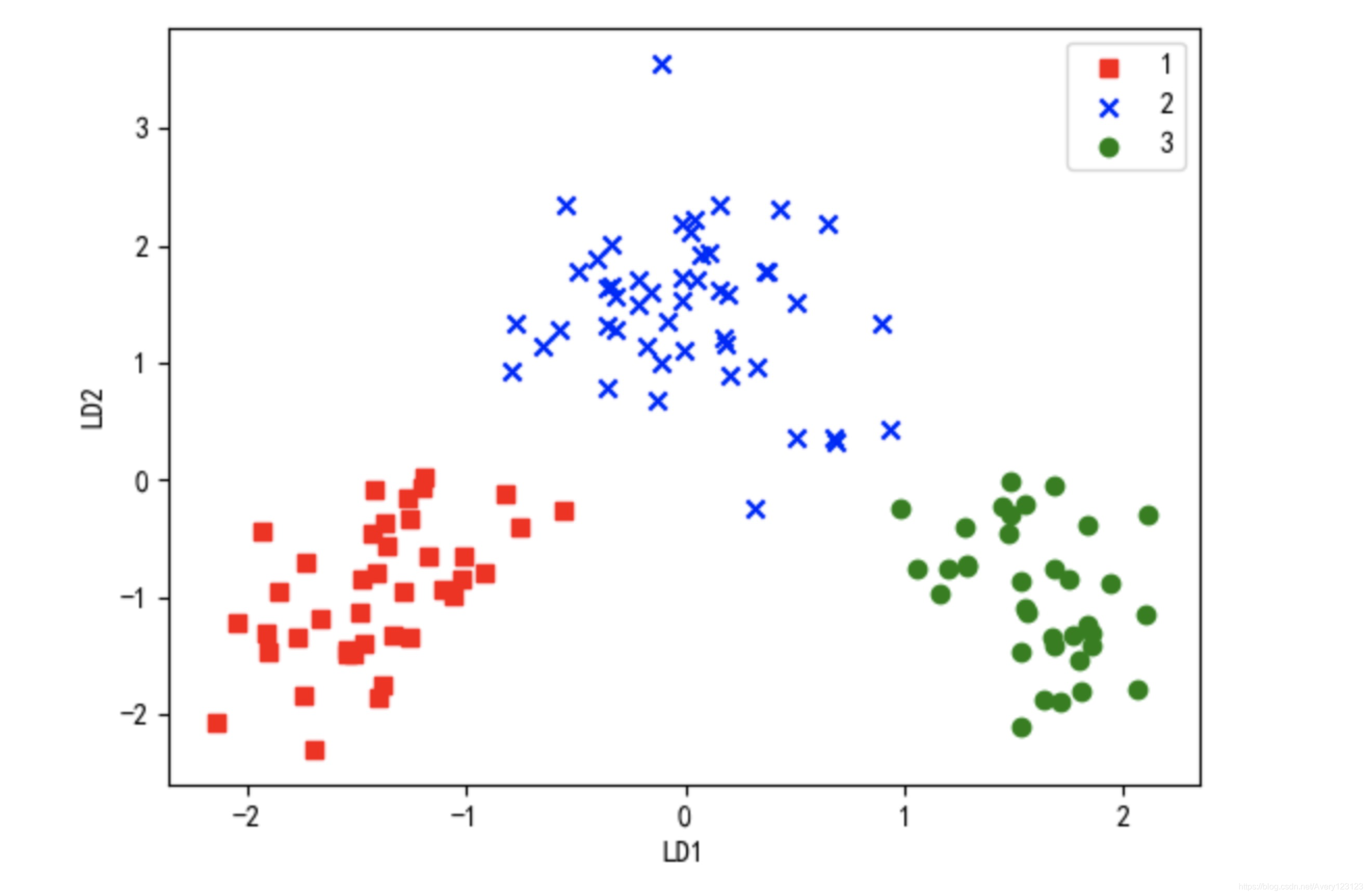
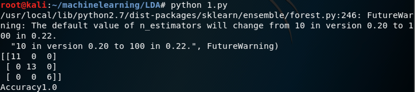
4.2 LDA implementation 2
github address: git@github.com:DengYangyong/LDA_gensim.git
常用函数:
- genism.doc2bow()方法,转化为单一向量。该方法只考虑词频,不考虑词语间的位置关系。
(1) slice。将分词后的字符串文档切分成词语列表。
(2) 构建词典dictionary。词典是所有文档所有单词的集合,并且记录了各词的出现次数。 <- 将词语映射到数字+只考虑词频。
Dictionary = corpora.Dictionary(text)
(3) 生成词典后,将其转化为向量形式。
Corpus = [dictionary.doc2bow(text) for text in texts]
<- genism内部用稀疏矩阵表示。因为单词总量极大,而一篇文档单词数有限,用密集矩阵来表示的话造成内存浪费。
4.3 Ida2vec implementation
essence本质:word2vec + document representation vector(来自于LDA而非paragraph vector)
LDA: topic distribution * each document's topic probability =each document representation vector
each topic vector is similar to word vectors in the same space
document vector is a weighted sum of topic vectors
lda2vec {word2vec: model word-to-word relationships
{LDA: model document-to-word relationships