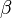提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档
文章目录
- 前言
- 一、LDA是什么?
- 二、公式推导
- 三、PCA和LDA的区别
- 总结
前言
线性判别分析(LDA)是一种有监督学习算法,同时经常被用来对数据进行降维。 它是1936年发明的,有些资料上也称之为Fisher LDA。LDA是目前机器学习、数据挖掘邻域中经典且热门的一种算法。提示:以下是本篇文章正文内容,下面案例可供参考
一、LDA是什么?
线性判别式分析,又称为Fisher线性判别。
找一个投影方向,使得把原来的类别投影到新的方向上,变成新的样本点,还能把它区分开。
准则:最大化类间均值,最小化类内方差
方差:方差小则样本不分散,更紧密。
不同类别间距离要大
二、公式推导
麻烦大家转一下手机,嘻嘻.


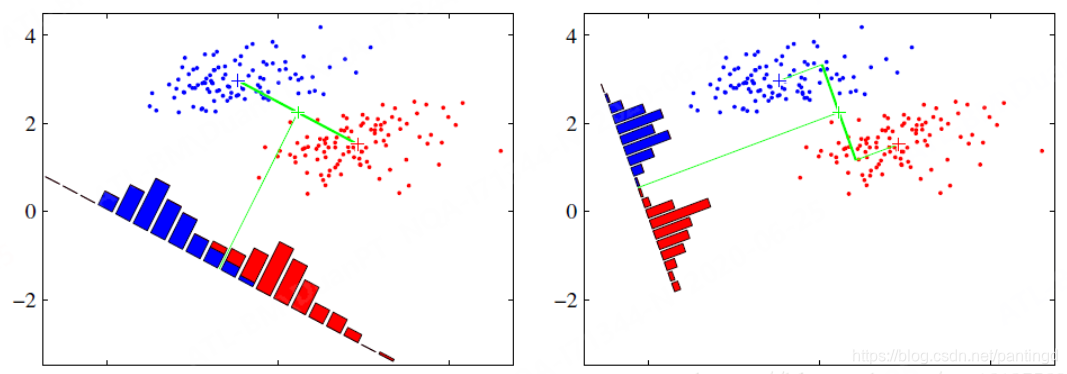
三、PCA和LDA的区别

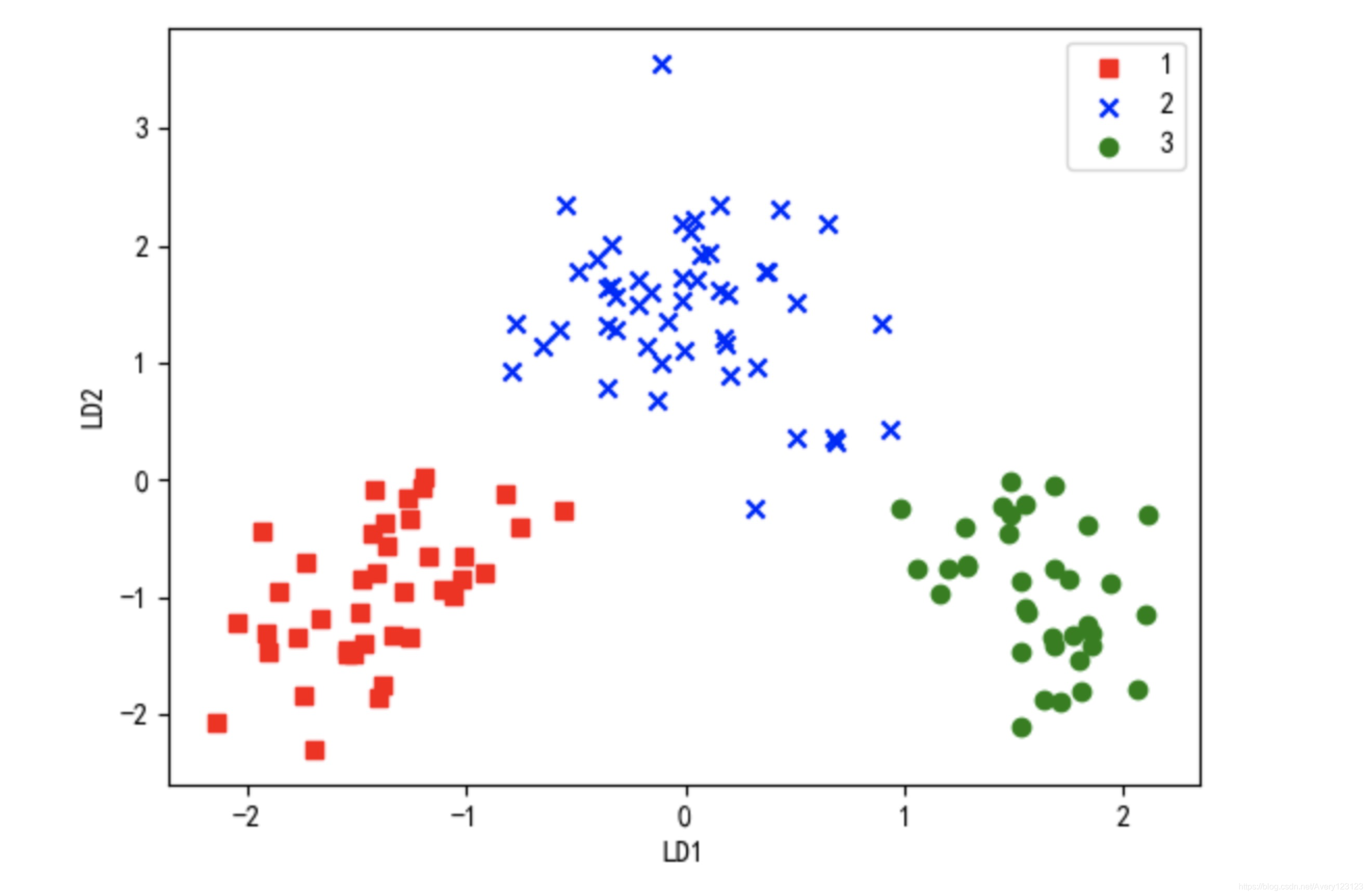
左图:PCA最小重构误差,使得投影后的值和原来的值尽量接近,属于非监督学习。
右图:LDA最大化类间距离,最小化类内距离,使得投影后的不同类别的样本分的更开,属于监督学习。
总结
提示:这里对文章进行总结:
至此,我们从最大化类间距离、最小化类内距离的思想出发,推导出了LDA的优化目标以及求解方法。LDA相比PCA更善于对有类别信息的数据进行降维处理,但它对数据的分布做了一些很强的假设,例如,每个类数据都是高斯分布、各个类的协方差相等。尽管这些假设在实际中并不一定完全满足,但LDA已被证明是非常有效的一种降维方法。主要是因为线性模型对于噪声的鲁棒性比较好,但由于模型简单,表达能力有一定局限性,我们可以通过引入核函数扩展LDA方法已处理分布较为复杂的数据。