目录
一、前言
二、什么是LDA?
三、LDA原理
1.二分类问题
2.多分类问题
3.几点说明
四、算法实现
一、前言
之前我们已经介绍过PCA算法,这是一种无监督的降维方法,可以将高维数据转化为低维数据处理。然而,PCA总是能适用吗?
考虑如下数据点:
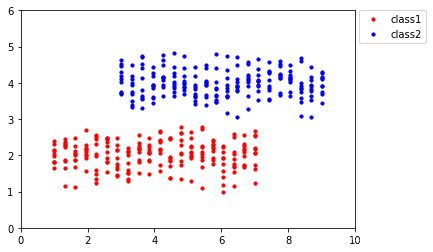
由PCA的原理我们可知,这些数据点在经PCA处理后会被映射到x轴上,如下所示:
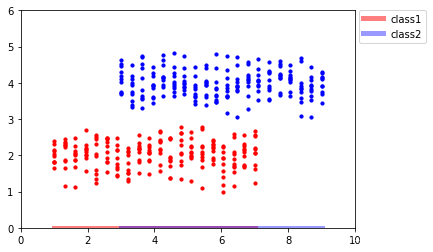
可以发现,投影后,红色数据点和蓝色数据点并不能很好地区分开。思考其背后的原因,在这个例子中,我们的数据点有了类别标签,而PCA是一种无监督学习算法,它会对所有类别的数据点 一视同仁,所以在分类问题中,PCA总是显得乏力。事实上,相比于X轴,将数据点投影到Y轴是一个更优选择:

如上图所示,将数据点投影到Y轴可以将两个类别的数据点很好地区分开来。那么我们该如何找到这种投影方式呢,下面我们将介绍一种新的降维方法——LDA算法。
二、什么是LDA?
线性判别分析(LDA),同PCA类似,也是一种降维算法,不一样的是,LDA是一种监督算法,它需要用到类别信息。LDA算法的思路同PCA一致,即通过某种线性投影,将原本高维空间中的一些数据,映射到更低维度的空间中,但LDA算法要求投影后的数据满足:1.同类别的数据之间尽可能地接近。2.不同类别的数据之间尽可能地远离。
三、LDA原理
1.二分类问题
从最简单的二分类问题开始讨论。根据LDA的投影目标,我们可以得到我们要优化的目标如下:
其中,代表投影后两个类别的数据的中心点,
代表投影后两个类别的数据的标准差。同PCA一致,我们一般用方差来表示数据的离散散程度,观察优化目标
,分子衡量的是投影后两个类别的数据中心点的距离,而分母衡量的是投影后两个类别的数据各自的离散程度。同类别的数据越接近(LDA投影目标1),分母越小,
越大;不同类别的数据越远离(LDA投影目标2),分子越大,
越大,目标合理。
方便起见,设为原始数据点,
分别为原始数据的中心点,
为投影向量,则有:
优化目标即为:
不妨设,则
可简化为
。
对求导,应有:
化简,得:
等式两边同除以,得:
变形,得:
显然,这又是一个矩阵分解问题,是矩阵
的特征值,同时也是我们优化的目标,而
即为对应的特征值,也是投影向量,所以我们将矩阵分解得到的特征值从大到小排列,然后取最大的几个特征值对应的特征向量作为我们的投影向量。
观察式子,由于
,代入,得:
由于代表的是投影后两类数据中心点间的距离,我们可以用常数
代替,于是有:
对于投影向量,我们只需要求得它的方向,对于它的大小(缩放程度)并无要求,所以我们最终求得的投影向量
即为
。通过这种方法,我们并不需要对矩阵进行分解便能求得投影向量,大大减少了计算量。
2.多分类问题
对二分类问题进行推广,考虑多分类问题。同样,投影的目的仍是使得同类数据点尽可能近,不同类别的数据点尽可能远。这里需要对优化目标做适当改变,如下:
其中,和二分类问题一致,仍是第i类数据的中心点和标准差,而
则代表所有数据的中心,
代表第i个类别的数据个数。仔细观察,可以发现,目标
的分母仍为各类别数据投影后的离散程度,而分子则是投影后各类别数据中心距所有数据中心点的距离的加权平方和,同样是衡量不同类别数据点的分离程度。优化的目标同二分类问题一致,重点关注LDA投影目标,万变不离其宗。
以二分类问题为例进行验证,有:
同样,我们只需要知道投影的方向,所以对于常数项,其只控制投影后数据点的缩放,并不影响最终结果,可以忽略。可以发现,用多分类问题的公式计算出来的结果同二分类的计算公式完全一致。
3.几点说明
(1).维度必减少
PCA算法降维可以理解为旋转坐标轴,新的坐标下每条轴作为一个维度也即成分,对于差距不大的维度可以略去从而达到降维的目的,也就是说实际上PCA算法可以将N维数据仍然变换为N维数据,然后可视情况删减维度。但LDA算法不尽然,使用LDA算法时,新的坐标维度必会减少。
以二分类为例,观察式子,由于
,可知
为奇异矩阵(它的秩最多为C-1),从而可以知道
也必为奇异矩阵,所以它分解后必有一个特征值为0,我们只能得到C-1个投影向量,C为类别个数。
(2).投影后各维度之间不一定正交
不一定是实对称矩阵,所以它分解后得到的特征向量未必正交。
(3).可能无解
当样本点个数少于样本维度时,会变为奇异矩阵,无法求逆。在这种情况下可能需要先用PCA降维,再使用LDA。
(4).无法适用
LDA并不是万能的,当同类别数据组成对角时,如下所示:
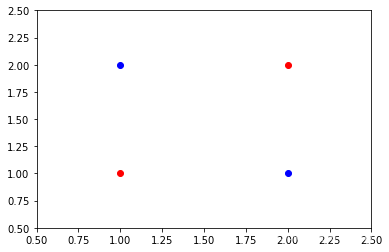
对于这种情况,我们可以发现,无论怎么投影均无法将两类数据点很好地区分开来。事实上,对于这种情况,普通的线性投影均束手无策,应该先增加维度再考虑区分。
此外,当不同类别的数据的中心重合,即时,有
=0,此时LDA也不再适用。
(5).对某些分类问题,PCA性能可能优于LDA
当数据重合度过高时,如下所示:
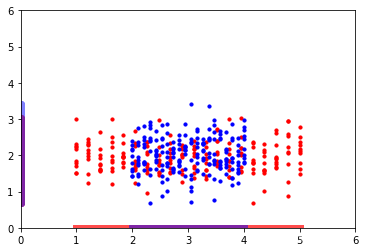
LDA会选择往Y轴方向进行投影,而PCA 由于不考虑类别信息,它会选择往X轴上进行投影。在这种情境下,PCA不失为一种更优选择。
四、算法实现
同样,根据前面的介绍,我们可以得到线性判别分析的一般步骤:给定样本,先中心化,然后求矩阵和
,再对矩阵
进行特征分解,代码实现如下:

当然,也可以不进行特征分解,直接套用公式 :

sklearn库里直接封装好了模型,可以直接使用:
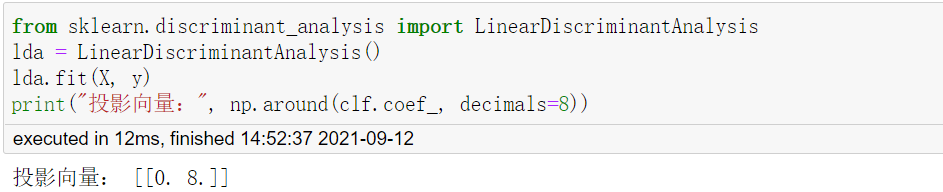
三种方法得到的特征向量分别为[0, -1],[0,-2],[0,8],标准化之后均为[0, 1],结果一致,即均投影到y轴上。观察特征分解结果,可以发现,有一个特征值为0,与前面对LDA的探讨一致。 ,
,