---

一、什么是页面置换算法？

进程运行时，若其访问的页面不在内存而需将其调入，但内存已无空闲空间时，就需要从内存中调出一页程序或数据，送入磁盘的对换区，其中选择调出页面的算法就称为页面置换算法。

好的页面置换算法应有较低的页面更换频率，也就是说，应将以后不会再访问或者以后较长时间内不会再访问的页面先调出

在地址映射过程中，若在页面中发现所要访问的页面不在内存中，则产生缺页中断。当发生缺页中断时，如果操作系统内存中没有空闲页面，则操作系统必须在内存选择一个页面将其移出内存，以便为即将调入的页面让出空间。而用来选择淘汰哪一页的规则叫做页面置换算法。

二、常用的页面置换算法

1. FIFO(先进先出算法)

(优先淘汰最早进入内存的页面)

FIFO算法是最简单的页面置换算法。FIFO页面置换算法为每个页面记录了调到内存的时间，当必须置换页面时会选择最旧的页面

"FIFO算法当进程分配到的页面数增加时，缺页中断的次数可能增加也可能减少”

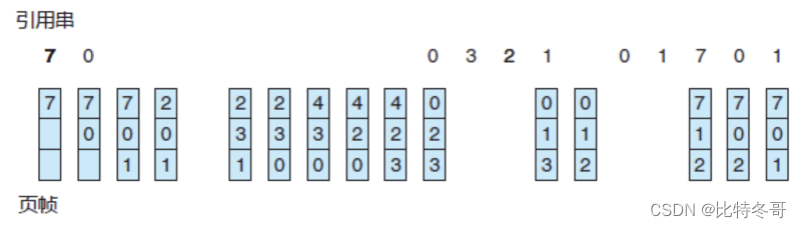
FIFO算法基于队列实现，不是堆栈类算法

注意，并不需要记录调入页面的确切时间，可以创建一个FIFO队列，来管理所有的内存页面。置换的是队列的首个页面。当需要调入页面到内存时，就将它加到队列的尾部

FIFO页面置换算法易于理解和编程。然而，它的性能并不总是十分理想:
（1）所置换的页面可以是很久以前使用过但现已不再使用的初始化模块
（2）所置换的页面可以包含一个被大量使用的变量，它早就初始化了，但仍在不断使用

2. OPT(最佳置换算法)

(淘汰以后不会使用的页面)

发现Belady 异常的一个结果是寻找最优页面置换算法，这个算法具有所有算法的最低的缺页错误率，并且不会遭受Belady 异常。这种算法确实存在，它被称为OPT 或 MIN

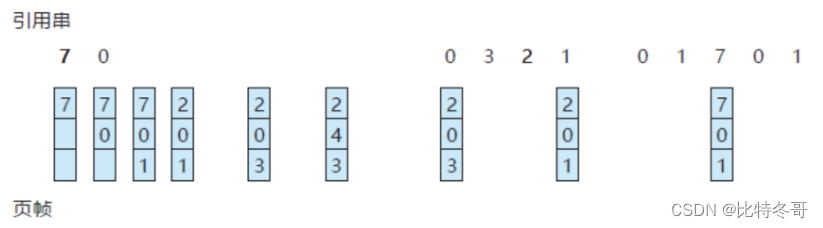
这种页面置换算法确保对于给定数量的帧会产生最低的可能的缺页错误率

FIFO和OPT算法的区别在于:除了在时间上向后或向前看之外，FIFO算法使用的是页面调入内存的时间，OPT算法使用的是页面将来使用的时间

3. LRU(最近最少使用算法)

(淘汰最近没有使用的页面)

选择最近最长时间未访问过的页面予以淘汰，它认为过去一段时间内未访问过的页面，在最近的将来可能也不会被访问。该算法为每个页面设置一个访问字段，来记录页面自上次被访问以来所经历的时间，淘汰页面时选择现有页面中值最大的予以淘汰

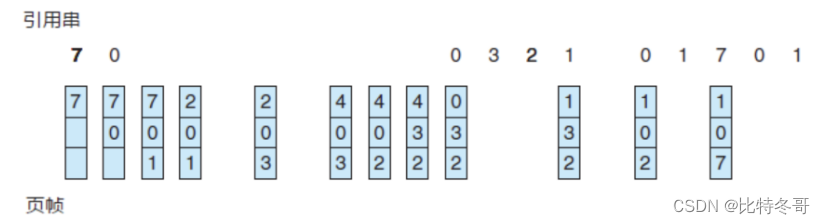
OPT和LRU算法的区别在于:LRU算法根据各页以前的情况，是"向前看"的，而最佳置换算法则根据各页以后的使用情况，是"向后看"的

LRU 性能较好，但需要寄存器和栈的硬件支持
LRU是堆栈类的算法，理论上可以证明，堆栈类算法不可能出现 Belady异常

4. Clock(时钟置换算法)

简单的CLOCK算法是给每一帧关联一个附加位，称为使用位。

当某一页首次装入主存时，该帧的使用位设置为1;
当该页随后再被访问到时，它的使用位也被置为1。

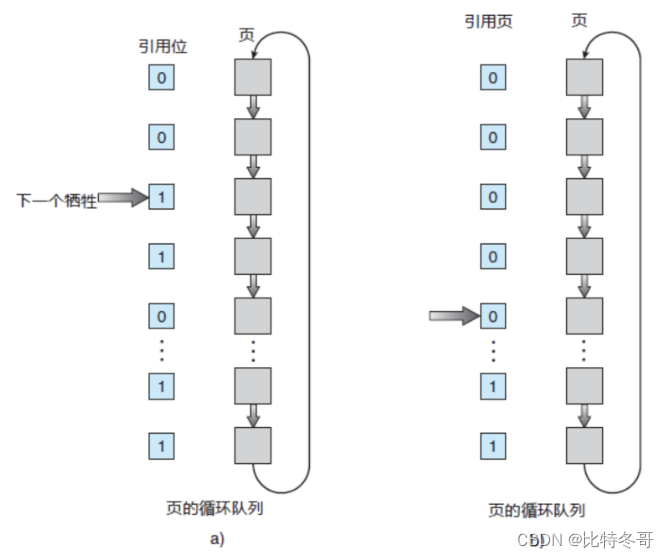
对于页替换算法，用于替换的候选帧集合看做一个循环缓冲区，并且有一个指针与之相关联。
当某一页被替换时，该指针被设置成指向缓冲区中的下—帧。
当需要替换一页时，操作系统扫描缓冲区，以查找使用位被置为0的一帧。
每当遇到一个使用位为1的帧时，操作系统就将该位重新置为0;

如果在这个过程开始时，缓冲区中所有帧的使用位均为0，则选择遇到的第一个帧替换;
如果所有帧的使用位均为1,则指针在缓冲区中完整地循环一周，把所有使用位都置为0，并且停留在最初的位置上，替换该帧中的页。

由于该算法循环地检查各页面的情况，故称为CLOCK算法，又称为最近未用( NotRecently Used,NRU )算法。

5. LFU(最不常用算法)

最不经常使用(LFU)页面置换算法要求置换具有最小计数的页面。

这种选择的原因是，积极使用的页面应当具有大的引用计数。然而，当一个页面在进程的初始阶段大量使用但是随后不再使用时，会出现问题。由于被大量使用，它有一个大的计数，即使不再需要却仍保留在内存中。一种解决方案是，定期地将计数右移1位，以形成指数衰减的平均使用计数。

6. MFU(最常使用算法)

最经常使用(MFU)页面置换算法是基于如下论点:具有最小计数的页面可能刚刚被引入并且尚未使用。
MFU和LFU置换都不常用。这些算法的实现是昂贵的，并且它们不能很好地近似OPT置换。

三、程序设计

#include<stdio.h>
#include<stdlib.h>
#define PN 12//页面访问列长度
#define FN 3//分配给进程的内存块数int *pageSeq;//页面访问序列
int *frames;//内存块数组
int fault,exchange;//缺页次数和置换次数
float ratio;//缺页率void init();//初始化页面访问向量
void clear();//初始化内存块
void print();//输出最后结果
void print1(int);//输出每一步结果
void OPT(int*,int,int*,int);//OPT算法
void FIFO(int*,int,int*,int);//FIFO算法
void LRU(int*,int,int*,int);//LRU算法
int search(int,int*,int,int);//搜索页面在序列某段中的位置，找到返回下标，否则返回-1int main()
{
int num;
printf("【页面置换算法】\n");
printf("序列长度：%d\n",PN);
printf("内存块数：%d\n",FN);
printf("======================\n\n");init();//初始化页面访问向量printf("操作说明：\n");printf("    num=0  程序结束\n");printf("    num=1  OPT算法\n");printf("    num=2  FIFO算法\n");printf("    num=3  LRU算法\n");printf("==============================\n");printf("\n");printf("输入操作序号num：");scanf("%d",&num);while(1){switch(num){case 0:printf("\n=====程序结束！=====\n");return 0;case 1:printf("\n【OPT算法】\n");OPT(pageSeq,PN,frames,FN);break;case 2:printf("\n【FIFO算法】\n");FIFO(pageSeq,PN,frames,FN);break;case 3:printf("\n【LRU算法】\n");LRU(pageSeq,PN,frames,FN);break;default:printf("\n=====重新输入=====\n");goto L1;}print();
L1:     printf("\n");printf("输入操作序号num：");scanf("%d",&num);}
}void init()//输入访问序列
{int i;pageSeq=(int*)(malloc(PN*sizeof(int)));frames=(int*)(malloc(FN*sizeof(int)));printf("向pageSeq输入页面访问序列：");for(i=0;i<PN;i++)scanf("%d",&pageSeq[i]);printf("\n");printf("页面访问序列：\n\n");//输出页面访问序列for(i=0;i<PN;i++)printf("%3d",pageSeq[i]);printf("\n\n");printf("===============================================================\n");
}void clear()//重新初始化内存块frames，因为有0号页面，所以置-1
{int i;fault=0;//缺页次数exchange=0;//置换次数for(i=0;i<FN;i++)//内存块置-1frames[i]=-1;
}void print1(int flag)//flag为缺页标志，输出每一步结果
{int t;for(t=0;t<FN;t++)//每访问一个页面，都输出一次内存块（页面）printf("%3d",frames[t]);if(flag) printf("  fault");//在缺页位置标记“fault”printf("\n");
}void print()//输出最后结果
{exchange=fault-FN;ratio=(float)fault/PN*100;printf("------------------------------\n");printf("缺页次数：%d\n",fault);printf("置换次数：%d\n",exchange);printf("缺 页 率：%4.1f%%\n",ratio);printf("==============================\n");
}int search(int p,int* ar,int start,int end)//参数说明：(页号，页面访问序列或者内存块数组，起点，终点)
{//检测页面p是否存在数组ar中(起点start，终点end)，存在则返回其在ar中的位置(下标)，否则返回-1int i,f;if(start>end)f=-1;//f作为方向标志，f=1时，循环变量递增；f=-1时，循环变量递减else f=1;i=start;//从strat位置开始搜索while(i!=end+f)//i超过end时结束循环{//在OPT算法中，start<end，循环变量递增，f=1；而在LRU算法中则相反，f=-1if(p==ar[i])return i;//首次搜索到p即返回下标i=i+f;}return -1;//未搜索到页面p，即p在未来不再被访问
}void OPT(int* arp,int p,int* arf,int f)
{//参数说明：(页面访问序列数组，数组长度，内存块数组，数组长度)int i=0,j,flag;int kf=0;//kf为进入内存页面数，当kf>=f时，内存块满，此时缺页产生置换，且kf的值不再增加int kp;//搜索起点，即页面访问序列中当前页的下一位置int posi,pmaxi,pmaxj;//未来最久不使用页面在arp和arf中的位置clear();//内存块数据清零printf("页面访问过程：\n");printf("------------------------------\n");for(i=0;i<p;i++)//扫描页面序列{flag=0;//缺页标志，初值置0，不缺页if(search(arp[i],arf,0,f-1)==-1)//页不在内存{flag=1;//缺页，flag置1fault++;//缺页+1if(kf<f)//有空闲内存块，无置换{arf[kf]=arp[i];//页面直接调入内存块arf[kf]中kf++;//当内存块放满页面后，kf不再增加}else//没有空闲内存块，将产生置换{kp=i+1; //设置页面访问序列arp中向后搜索的起点，选择淘汰页面pmaxi=-1;//被淘汰页面在访问序列arp中的位置，初值置-1for(j=0;j<f;j++){//对内存arf中的每个页面依次查找其在访问序列arp中（未来）第一次出现的位置，并存放在posi中posi=search(arf[j],arp,kp,p-1);if(posi==-1)//search()返回-1，说明该页面在未来不存在，即不会再被访问到{arf[j]=arp[i];//置换并终止循环break;}if(posi>pmaxi){//search()返回值不是-1，则记录最久未使用页面在访问序列arp中的位置pmaxi=posi;//记录最大位置pmaxj=j;//记录最久未使用页面在内存arf中的位置}}if(j>=f)arf[pmaxj]=arp[i];//当内存块数组arf中所有页面在未来都会被访问到时，置换}}print1(flag);//输出一次内存页面情况}
}void FIFO(int* arp,int p,int* arf,int f)
{//参数说明：(页面访问序列数组，数组长度，内存块数组，数组长度)int i,j=0,flag;clear();//内存块数据清零printf("页面访问过程：\n");printf("------------------------------\n");for(i=0;i<p;i++){flag=0;//缺页标志，同OPTif(search(arp[i],arf,0,f-1)==-1)//如果当前页面arp[i]不在内存{fault++;//缺页+1flag=1;arf[j]=arp[i];//页面调入内存j=(j+1)%f;//j+1，循环}print1(flag);//输出一次内存页面情况}
}void LRU(int* arp,int p,int* arf,int f)
{//参数说明：(页面访问序列数组，数组长度，内存块数组，数组长度)int i,j;int kf=0;//kf>=f时，内存块满，此时缺页产生置换int flag;//缺页标志int pmini,pminj;//最久未访问页面在arp[]中过去的位置和在arf[]中的位置int posi;clear();//清理内存块数据等for(i=0;i<p;i++){flag=0;if(search(arp[i],arf,0,f-1)==-1)//页面不在内存{flag=1;fault++;//缺页if(kf<f)//有空闲块，无置换{arf[kf]=arp[i];kf++;}else//无空闲块，产生置换{//在arp[]中向前搜索，寻找最久未被访问的页面位置pmini=p;//pmini值初值（最大值或者当前值i）for(j=0;j<f;j++){posi=search(arf[j],arp,i-1,0);//这里与OPT不同，不会出现页面不存在的情况if(posi<pmini){pmini=posi;pminj=j;}}arf[pminj]=arp[i];//置换}}print1(flag);//输出一次内存页面情况}
}