目录
- Echo State Network
- ESN的训练与预测
- 关于ESN工作原理的理解
- 基于Numpy的ESN
Echo State Network
ESN的训练与预测
回声状态网络(Echo State Network)又称为库计算,即Reservoir Computing,被视为是一种神经网络的扩展。
Reservoir Computing 多用于处理时间序列的预测问题,比如下图:

给定一个信号序列: u ( 0 ) , u ( 1 ) , . . . , u ( N t − 1 ) \textbf{u}(0),\textbf{u}(1),...,\textbf{u}(N_{t}-1) u(0),u(1),...,u(Nt−1)给定一个target序列: v ( 1 ) , v ( 2 ) , . . . , v ( N t ) \textbf{v}(1),\textbf{v}(2),...,\textbf{v}(N_{t}) v(1),v(2),...,v(Nt)要求学习一个black box模型,该模型能够预测出序列: v ( N t + 1 ) , v ( N t + 2 ) , . . . \textbf{v}(N_{t}+1),\textbf{v}(N_{t}+2),... v(Nt+1),v(Nt+2),...注意到,在符号表述上增加了粗体,用于表示向量,比如 u ( 0 ) \textbf{u}(0) u(0)可以是一个向量。
当然, u ( 0 ) \textbf{u}(0) u(0)可以是一维的时间序列,也可以是多维的时间序列。
网络包括三个部分:输入 I I I,储备池 R R R,输出 O O O。
假设输入为 M M M维向量,储备池内为 N N N维向量,输出为 L L L维向量。因此,输入到储备池的映射矩阵为 W I R ∈ R N × M W_{IR}\in R^{N\times M} WIR∈RN×M,储备池到输出的映射矩阵为 W R O ∈ R L × N W_{RO}\in R^{L\times N} WRO∈RL×N。储备池内部与前一时刻的储备池和输入关联: r ( t + 1 ) = f [ W r e s ⋅ r ( t ) + W I R ⋅ u ( t ) ] \textbf{r}(t+1)=f[W_{res}\cdot\textbf{r}(t)+W_{IR}\cdot\textbf{u}(t)] r(t+1)=f[Wres⋅r(t)+WIR⋅u(t)]其中, f f f是激活函数,一般为 t a n h tanh tanh, W r e s W_{res} Wres是储备池内部的连接关系,通常随机初始化为一个稀疏矩阵。
W r e s ∈ R N × N W_{res}\in R^{N\times N} Wres∈RN×N有邻接矩阵的含义,反映了向量 r ( t ) \textbf{r}(t) r(t)内各个元素的连接关系,表达了一个图结构。
网络输出为 W R O ⋅ r ( t ) W_{RO}\cdot\textbf{r}(t) WRO⋅r(t)。
回声状态网络的训练属于监督学习,损失函数为: L = ∑ t = d + 1 N t ∣ v ( t ) − W R O ⋅ r ( t ) ∣ 2 + η ∣ W R O ∣ 2 L=\sum_{t=d+1}^{N_{t}}|\textbf{v}(t)-W_{RO}\cdot\textbf{r}(t)|^{2}+\eta|W_{RO}|^{2} L=t=d+1∑Nt∣v(t)−WRO⋅r(t)∣2+η∣WRO∣2第二项为正则化项,用于避免过拟合。
从 d + 1 d+1 d+1步开始计算损失,是为了让储备池经过前 d d d次计算达到稳定状态,这与回声状态网络仅训练 W R O W_{RO} WRO的特性相关。
由于仅学习参数 W R O W_{RO} WRO,可以不采用梯度下降迭代就直接得到其解析解: W R O = V R T ( R R T + η I ) − 1 W_{RO}=VR^{T}(RR^{T}+\eta I)^{-1} WRO=VRT(RRT+ηI)−1其中, V V V和 R R R是向量 v ( t ) \textbf{v}(t) v(t)和 r ( t ) \textbf{r}(t) r(t)沿时间的堆叠表示。
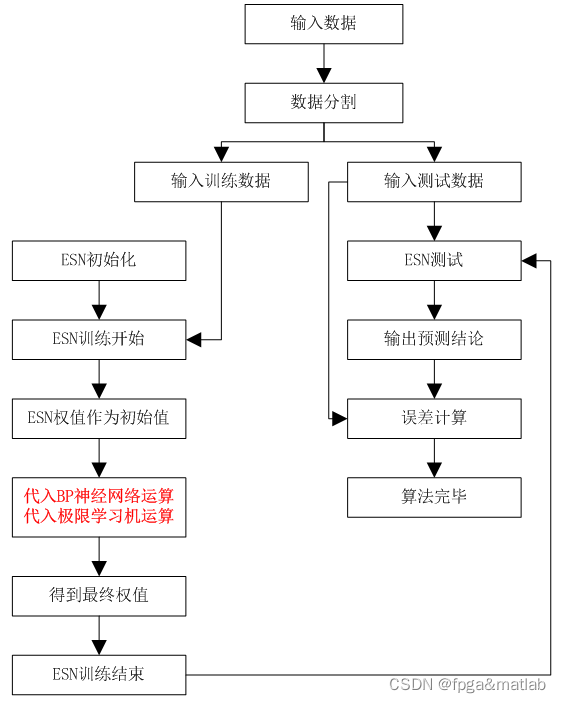
关于时间序列预测,通常,我们将输出再作为输入,从而实现不断地向后预测,因此有以下计算过程:
- 1.将输出作为输入: u ( t ) = W R O ⋅ r ( t ) \textbf{u}(t)=W_{RO}\cdot\textbf{r}(t) u(t)=WRO⋅r(t)
- 2.计算下一时刻的储备池: r ( t + 1 ) = t a n h [ W r e s ⋅ r ( t ) + W I R ⋅ u ( t ) ] \textbf{r}(t+1)=tanh[W_{res}\cdot\textbf{r}(t)+W_{IR}\cdot\textbf{u}(t)] r(t+1)=tanh[Wres⋅r(t)+WIR⋅u(t)]
- 3.将该时刻输出作为新的输入: u ( t + 1 ) = W R O ⋅ r ( t + 1 ) \textbf{u}(t+1)=W_{RO}\cdot\textbf{r}(t+1) u(t+1)=WRO⋅r(t+1)
- 4.回到第2步依次循环。
额外补充关于ESN中关于储备池的初始化内容:
- 热启动(warm start):在预测时,初始储备池 r ( t + 1 ) \textbf{r}(t+1) r(t+1)需要使用到 r ( t ) \textbf{r}(t) r(t),热启动可以使用训练结束时的储备池状态作为 r ( t ) \textbf{r}(t) r(t);
- 冷启动(cold start):将 r ( t ) \textbf{r}(t) r(t)初始化为零,结合初始输入信息得到初始的储备池状态 r ( t + 1 ) \textbf{r}(t+1) r(t+1)。
关于ESN工作原理的理解
Echo State Network提出于2001年,曾经是研究的热点,近年来随着RNN,LSTM与其它一些变种网络的出现,现在的相关研究越发减少,但是其在时间序列预测上依然有着很不错的应用。
传统的MLP网络的隐层是一层层的全连接的神经元,而ESN引入了一个储备池计算模式来替代MLP的隐层。
储备池的特点是:
- 储备池中神经元的连接状态是随机的,即神经元之间是否建立连接并不是我们人工确定的;
- 储备池中的连接权重是固定的,不像传统的MLP网络使用梯度下降进行权重的更新。这样做的好处是:(1)大大降低了训练的计算量;(2)一定程度上避免了梯度下降的优化算法中出现的局部最优情况。
ESN的基本思想就是由储备池生成一个随输入不断变化的复杂动态空间,当这个状态空间足够复杂时,就可以利用这些内部状态,再线性组合处所需要的对应输出。从而实现经典网络MLP拟合数据的能力。
基于Numpy的ESN
ESN的可学习参数仅有 W R O W_{RO} WRO,而 ( W I R , W r e s , η ) (W_{IR},W_{res},\eta) (WIR,Wres,η)均为超参数。
通常,我们随机从 [ − α , α ] [-\alpha,\alpha] [−α,α]均匀分布中生成 W I R W_{IR} WIR,一般来说, W I R W_{IR} WIR对网络的效果影响较小。
关于储备池内部的关系 W r e s W_{res} Wres,相当于一个邻接矩阵, N N N的值往往大于 M M M。 W r e s W_{res} Wres通常是一个稀疏的图结构。
经验上,我们可以通过谱半径(关于矩阵特征值的绝对值集合,当中的最大者)检验 W r e s W_{res} Wres对网络的影响。(注意,有些论文认为谱半径大于1是好的,而有些论文又表明谱半径小于1是好的)
下面是Numpy实现的ESN(本次实现是简单的demo,仅用于标量计算),使用数据集为Mackey-Glass (MG)序列,这个时间序列是混乱的,没有明确的周期。 级数不收敛也不发散,轨迹对初始条件高度敏感。 这个基准问题用于神经网络和模糊建模研究。数据集存放在个人资源处。
首先导入相关包:
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
下面认识数据集:
data = np.load('mackey_glass_t17.npy')print(data.shape) # (10000,)# 可视化前2000个数据
mylen = 2000
plt.figure(figsize=(12, 4))
plt.plot(np.arange(mylen), data[:mylen])
可视化结果为:

调整数据集形状:
# 调整形状
data = np.reshape(data, (1, data.shape[0]))
print(data.shape) # (1, 10000)
定义并初始化相关参数:
# 设置随机种子
np.random.seed(2050)N = 1000 # 储备池r(t)的规模
rho = 1.36 # 谱半径spetral radius
sparsity = 3/N # 用于设置稀疏矩阵
N_t = 2000 # 训练数据的容量
N_tp = 1000 # 测试数据的容量
d = 200 # 过度至稳定状态的前d步
eta = 1e-4# 参数初始化
W_IR = np.random.rand(N, 1) * 2 - 1 # [-1, 1] 的均匀分布,参数形状为(N,1)W_res = np.random.rand(N, N) # [0,1]的均匀分布,参数形状为(N,N)
W_res[W_res > sparsity] = 0
W_res = W_res / np.max(np.abs(np.linalg.eigvals(W_res))) * rho # 重置谱半径
训练模型,其本质是计算参数 W R O W_{RO} WRO:
# 训练
r = np.zeros((N, N_t+1)) # 历代储备池 (N,N_t+1)
u = data[:, :N_t] # 训练数据尺寸(1, N_t)# 叉乘:矩阵相乘,矢量积;点乘:两个矩阵的元素一一对应相乘
# tf.matmul(A,C)=np.dot(A,C)= A@C属于叉乘
# tf.multiply(A,C)=A*C属于点乘
for t in range(N_t):r[:, t+1] = np.tanh(W_res @ r[:, t] + W_IR @ u[:, t])rp = r[:, d+1:] # 去除前d步
v = data[:, d+1:N_t+1] # 取target序列
W_RO = v @ rp.T @ np.linalg.pinv(rp @ rp.T + eta * np.identity(N))
热启动并预测:
# 预测
u_pred = np.zeros((1, N_tp))
r_pred = np.zeros((N, N_tp))
r_pred[:, 0] = rp[:, -1] # 热启动warm start
for step in range(N_tp-1):u_pred[:, step] = W_RO @ r_pred[:, step]r_pred[:, step+1] = np.tanh(W_res @ r_pred[:, step] + W_IR @ u_pred[:, step])
计算误差,并可视化对比预测结果与真实序列:
# 计算误差
error = np.sqrt(np.mean((u_pred - data[:, N_t:N_t+N_tp])**2))
print(error) # 0.09937755711160892# 可视化对比
plt.figure(figsize=(12, 4))
plt.plot(u_pred.T, 'r', label='predict', alpha=0.6)
plt.plot(data[:, N_t:N_t+N_tp].T, 'b', label='True', alpha=0.6)
plt.legend(fontsize=16)
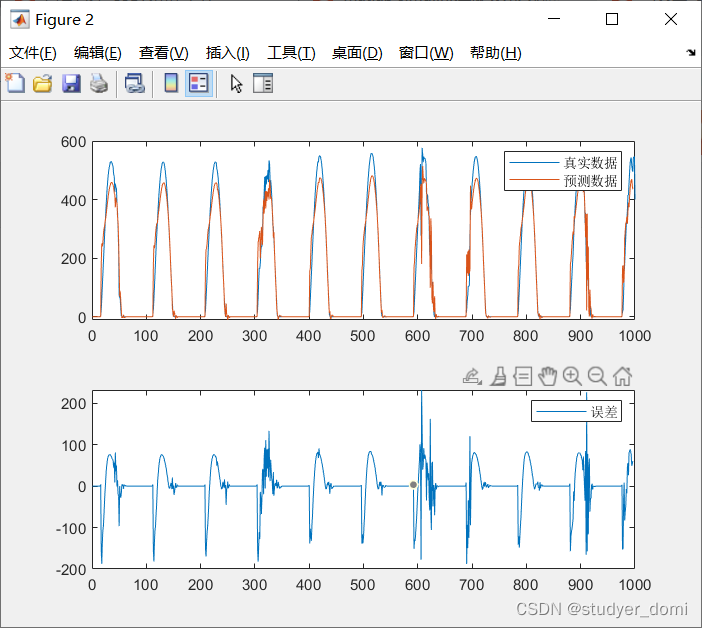
预测结果与真实序列的对比如下:

误差计算结果为:0.09937755711160892。