一、提出

循环神经网络（Recurrent Neural Networks,RNNs）的训练是通过反向对权值直接优化来实现的，这种方式容易产生两个问题：收敛速度慢和易陷入局部最优。回声状态网络( echo state network，ESN) 由 Jaeger于2001年提出，在模型构建与学习算法方面较传统的循环神经网络有较大差别，凭借不同于循环神经网络反向传播的形式进行学习，其相应的学习算法为递归神经网络的研究开启了新纪元。

回声状态网络又称储备池计算（RC，reservoir computing），采用由随机生成稀疏连接固定不变的内部权重矩阵得到神经元组成的储备池作为隐层，用以将输入进行投射到高维、非线性的表示。ESN将神经网络的隐层权值预先生成而非训练生成，与隐层至输出层的权值训练分开进行，其基本思想的前提是生成的储备池具有某种良好的属性，往往能够保证仅采用线性方法训练储备池至输出层的权值即可获得优良的性能。

二、基本原理

2.1 网络结构

ESN拓扑结构图

基本方程：

预先生成Win(输入单元与储备池内部连接权值矩阵)、W(储备池内部连接权值矩阵)、Wback(储备池与输出单元连接权值矩阵)，只训练Wout(储备池与输出单元连接权值矩阵)

$\small f$ :储备池单元的激活函数

$\small f^{out}$ :输出单元的激活函数

2.2 主要参数

2.2.1 储备池规模N

储备池其中神经元的个数N，常规来讲N值越大，预测的精度越高，但同时也会导致效率低下，容易过拟合。

2.2.2 储备池谱半径SR

SR是W最大特征值的绝对值，是影响储备池记忆能力的主要因素。一般需要保证SR<1，ESN才有回声状态性质，但后续研究逐步超越该界限，SR<1的要求不再严格。

2.2.3 储备池稀疏程度SD

SD是内部神经元的连接情况，表示储备池中相互连接的神经元占所有神经元总数的比例，通常为1%~5%。

2.2.4 输入单元尺度IS

IS是输入连接至储备池之前需要相乘的一个尺度因子。相乘使得输入信号变换至神经元激活函数相应的范围内。

2.3 构造方法

ESN的建立流程

（1）首先确定储备池的规模，即神经元的个数。节点数越多，拟合能力越强。由于ESN仅仅通过调整输出权值来线性拟合输出结果，所以一般ESN需要远大于常规神经网络的节点规模。
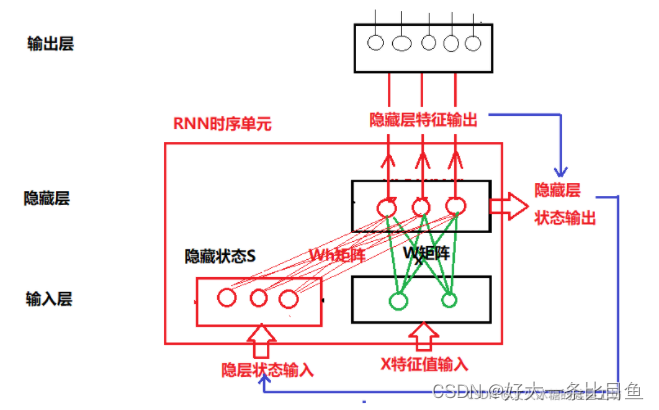
（2）随机生成连接矩阵W，这个矩阵表示了哪些神经元之间是有连接的，以及连接的方向和权值。此处往往使新接触ESN的同学存疑，并因此对ESN的储备池不太理解。事实上，内部权重矩阵是某时刻神经元与下一时刻神经元的连接，而非普通的互相连接，若对此有疑问，需回看循环神经网络，在此引用https://blog.csdn.net/HiWangWenBing/article/details/121387285，图片可供参考。

（3）其次是输入连接的权值大小以及内部连接矩阵的谱半径，这些关键参数会影响到网络短期记忆时间的长短，输入权值越小而内部矩阵的谱半径越接近1，网络短期记忆时间越长。但是增强记忆能力的同时，这种操作也造成了网络对“快速变化”系统建模能力下降。在实际应用中，要通过分析被建模系统的实际变化特征来选取相应的数值。

2.4 训练过程

2.4.1 采集状态

采样阶段即将输入数据经过输入连接权重、储备池、初始输出权重得到各个时刻的输出 y ( n），在此阶段需要把储备池的内部状态不断收集，为后续的训练做准备。

for t in range(trainLen):u = data[t]x = (1 - a) * x + a * tanh(dot(Win, vstack((1, u))) + dot(W, x))  # vstack((1, u)):将偏置量1加入输入序列if t >= initLen:  # 空转100次后，开始记录储备池状态X[:, t - initLen] = vstack((1, u, x))[:, 0]

从代码中容易理解，随着时间t的增长，输入数据不断传入，同时储备池状态持续更新，更新的过程中记录下储备池状态。空转100次的目的是缓冲随机生成状态造成的影响。

2.4.2 权值计算

为了实现权值的计算，需要根据在采样阶段收集到系统状态矩阵X和目标输出y，计算输出连接权 W out 。因为状态变量 x （ n）和系统输出 y （ n）之间是线性关系，而需要实现的目标是利用网络实际输出 y （ n）逼近期望输出 y （ n），即

也就是希望计算权值 Wout ，数学上讲这是一个线性回归问题，可使用常用的线性回归算法快速求解。

# 使用Wout根据输入值和储备池状态去拟合目标值，这是一个简单的线性回归问题，这里使用的是岭回归(Ridge Regression)。
reg = 1e-8  # 正则化系数
X_T = X.T
# Wout:  1 * 1+K+N
Wout = dot(dot(Yt, X_T), linalg.inv(dot(X, X_T) + \reg * eye(1 + inSize + resSize)))  # linalg.inv矩阵求逆；numpy.eye()生成对角矩阵，规模:1+inSize+resSize，默认对角线全1，其余全0

至此训练完成，使用时可直接使用上面训练完成的Wout进行输出预测值。

三、Python代码实现

from numpy import *
from matplotlib.pyplot import *
import scipy.linalg
import matplotlib.pyplot as plt# 加载数据
# 前2000个数据用来训练，2001-4000的数据用来测试。训练数据中，前100项用来初始化储备池，以让储备池中形成良好的回声之后再开始训练。
trainLen = 2000
testLen = 2000
initLen = 100  # 前100项用来初始化储备池data = loadtxt('MackeyGlass_t17.txt')# 绘制前1000条数据
figure(0).clear()
plot(data[0:1000])
title('A sample of data')# 生成ESN储层
inSize = outSize = 1  # inSize 输入维数 K
resSize = 1000  # 储备池规模 N
a = 0.3  # 可以看作储备池更新的速度，可不加，即设为1.random.seed(42)
# 随机初始化 Win 和 W
Win = (random.rand(resSize, 1 + inSize) - 0.5) * 1  # 输入矩阵 N * 1+K
W = random.rand(resSize, resSize) - 0.5  # 储备池连接矩阵 N * N# 对W进行防缩，以满足稀疏的要求。
# 方案 1 - 直接缩放 (快且有脏数据, 特定储层): W *= 0.135
# 方案 2 - 归一化并设置谱半径 (正确, 慢):
print('计算谱半径...')
rhoW = max(abs(linalg.eig(W)[0]))  # linalg.eig(W)[0]:特征值   linalg.eig(W)[1]:特征向量
W *= 0.9 / rhoW# 为设计（收集状态）矩阵分配内存
X = zeros((1 + inSize + resSize, trainLen - initLen))  # 储备池的状态矩阵x(t)：每一列是每个时刻的储备池状态。后面会转置
# 直接设置相应的目标矩阵
Yt = data[None, initLen + 1:trainLen + 1]  # 输出矩阵:每一行是一个时刻的输出# 输入所有的训练数据，然后得到每一时刻的输入值和储备池状态。
x = zeros((resSize, 1))
for t in range(trainLen):u = data[t]x = (1 - a) * x + a * tanh(dot(Win, vstack((1, u))) + dot(W, x))  # vstack((1, u)):将偏置量1加入输入序列if t >= initLen:  # 空转100次后，开始记录储备池状态X[:, t - initLen] = vstack((1, u, x))[:, 0]# 使用Wout根据输入值和储备池状态去拟合目标值，这是一个简单的线性回归问题，这里使用的是岭回归(Ridge Regression)。
reg = 1e-8  # 正则化系数
X_T = X.T
# Wout:  1 * 1+K+N
Wout = dot(dot(Yt, X_T), linalg.inv(dot(X, X_T) + \reg * eye(1 + inSize + resSize)))  # linalg.inv矩阵求逆；numpy.eye()生成对角矩阵，规模:1+inSize+resSize，默认对角线全1，其余全0
# Wout = dot( Yt, linalg.pinv(X) )# 使用训练数据进行前向处理得到结果
# run the trained ESN in a generative mode. no need to initialize here,
# because x is initialized with training data and we continue from there.
Y = zeros((outSize, testLen))
u = data[trainLen]
for t in range(testLen):x = (1 - a) * x + a * tanh(dot(Win, vstack((1, u))) + dot(W, x))y = dot(Wout, vstack((1, u, x)))  # 输出矩阵(1 * 1+K+N)*此刻状态矩阵(1+K+N * 1)=此刻预测值Y[:, t] = y  # t时刻的预测值   Y: 1 * testLen# 生成模型u = y# 预测模型# u = data[trainLen+t+1]# 计算第一个errorLen时间步长的MSE
errorLen = 500
mse = sum(square(data[trainLen + 1:trainLen + errorLen + 1] - Y[0, 0: errorLen])) / errorLen
print('MSE = {0}'.format(str(mse)))# 绘制测试集的真实数据和预测数据
figure(1).clear()
plot(data[trainLen + 1:trainLen + testLen + 1], 'g')
plot(Y.T, 'b')
title('Target and generated signals $y(n)$ starting at $n=0$')
legend(['Target signal', 'Free-running predicted signal'])# 绘制储备池中前200个时刻状态(x(t))的前20个储层结点值
figure(2).clear()
plot(X[0:20, 0:200].T)
title('Some reservoir activations $\mathbf{x}(n)$')# 绘制输出矩阵
figure(3).clear()
# bar(np.arange(1 + inSize + resSize), Wout.T, 8)
plot(np.arange(1 + inSize + resSize), Wout.T)title('Output weights $\mathbf{W}^{out}$')
show()

MackeyGlass_t17.txt - 蓝奏云，点击此连接获取数据集