转载自：https://zhuanlan.zhihu.com/p/25212301，本文只做个人记录学习使用，版权归原作者所有。

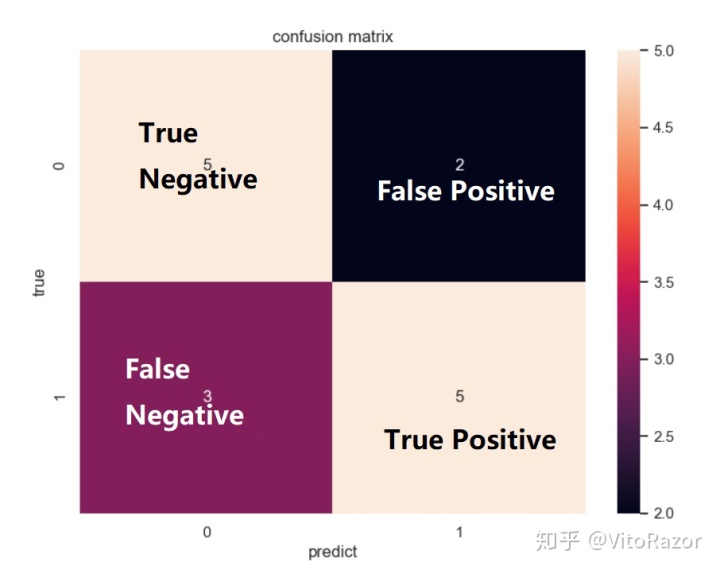
1、混淆矩阵

混淆矩阵如下图所示，分别用0和1代表负样本和正样本。FP代表实际类标签为0但是预测标签为1的样本数量，其余可类似推理。

2、假正率和真正率

假正率(False Positve Rate)是实际标签为0的样本中，被预测错误的比例。真正率(True Positive Rate)是实际标签为1的样本中被预测正确的比例，其公式如下：

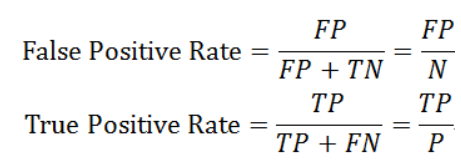
3、计算threshold=0.5上的混淆矩阵、假正率和真正率

假设我们通过训练集训练了一个二分类模型，在测试集上进行预测每个样本所属的类别，输出了属于类别1的概率。现在假设当P>=0.5时，预测的类标签为1.

（1）导入相关库

import pandas as pd
import matplotlib.pyplot as plt
import numpy as np#测试样本的数量
parameter=40

(2)随机生成结果集

data=pd.DataFrame(index=range(0,parameter),columns=('probability','The true label'))
data['The true label']=np.random.randint(0,2,size=len(data))
data['probability']=np.random.choice(np.arange(0.1,1,0.1),len(data['probability']))

结果如下：

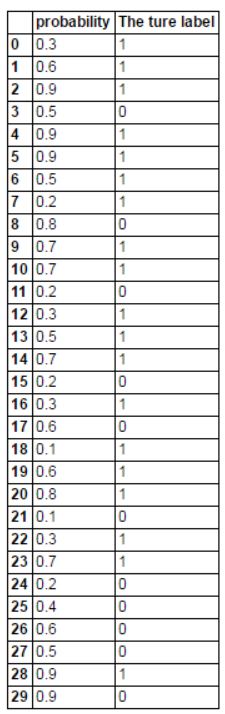
(3)计算混淆矩阵

cm=np.arange(4).reshape(2,2)
#TN
cm[0,0]=len(data[data['The true label']==0][data['probability']<0.5])
#FP
cm[0,1]=len(data[data['The true label']==0][data['probability']>=0.5])
#FN
cm[1,0]=len(data[data['The true label']==1][data['probability']<0.5])
#TP
cm[1,1]=len(data[data['The true label']==1][data['probability']>=0.5])

(4)计算假正率和真正率

import itertools
classes=[0,1]
plt.figure()
plt.imshow(cm,interpolation='nearest',cmap=plt.cm.Blues)
plt.title('Confusion matrix')
tick_marks=np.arange(len(classes))
plt.xticks(tick_marks,classes,rotation=0)
plt.yticks(tick_marks,classes)
thresh=cm.max()/2.
for i,j in itertools.product(range(cm.shape[0]),range(cm.shape[1])):plt.text(j,i,cm[i,j]),horizontalalignment="center",color="white" if cm[i,j]>thresh else "black"
plt.tight_layout()
plt.ylabel('True label')
plt.xlabel('Predicted label')

生成的threshold=0.5时候的混淆矩阵如下图所示：

然后，threshold=0.5的假正率FPR=6/(5+6)=0.55，真正率TPR=13/(13+6)=0.68

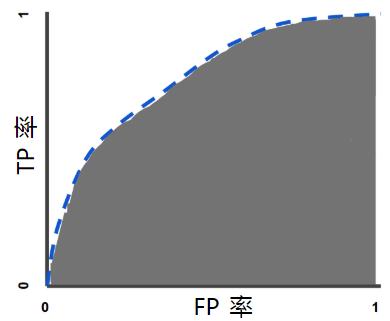
4.ROC曲线和AUC值

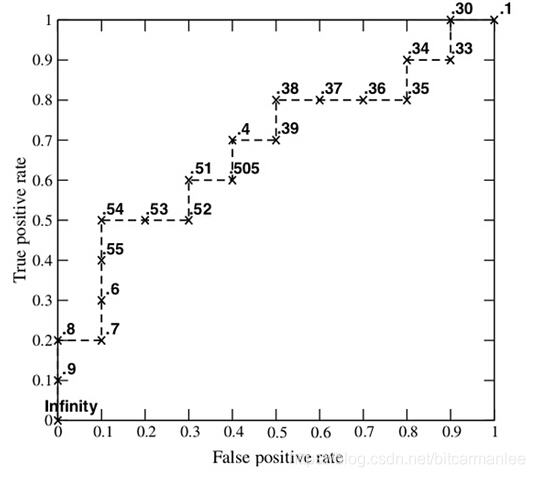
ROC曲线是一系列threshold下的(FPR,TPR)数值点的连线，此时的threshold的取值分别为测试数据集中各样本的测试概率，但，取各个概率的顺序是从大到小的。

(1)按照概率从大到小排序：

data.sort_values('probability',inplace=True,ascending=False)

排序结果如下：

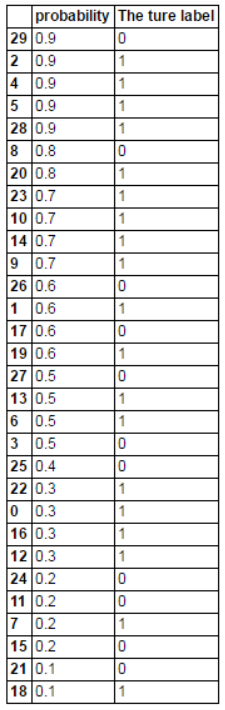
此时，threshold依次取0.9,0.9,0.9,0.9,0.9,0.9,0.8,0.8,0.7,....比如，当threshold=0.9(第3个0.9)，一个“0”预测错误，两个“1”预测正确，FPR=1/11=0.09，TPR=2/19=0.11.当threshold=0.9(第5个0.9)，一个“0”预测错误，四个“1”预测正确，FPR=1/11=0.09，TPR=4/19=0.21,以此类推。

(2)计算全部概率值下的FPR和TPR

TPRandFPR=pd.DataFrame(index=range(len(data)),columns('TP','FP'))
for j in range(len(data)):data1=data.head(n=j+1)FP=len(data1[data1['The true label']==0][data1['probability']>=data1.head(len(data1))[probability]])/float(len(data[data['The true label']==0]))TP=len(data1[data1['The true label']==1][data1['probability']>=data1.head(len(data1))['probability']])/float(len(data[data['The true label']==1]))TPRandFPR.iloc[j]=[TP,FR]

最后，threshold分别取样本中各个概率值时的FPR和TPR的点矩阵如下：

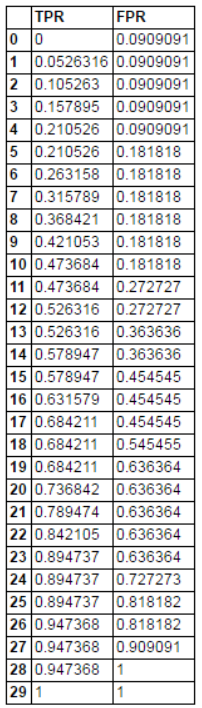
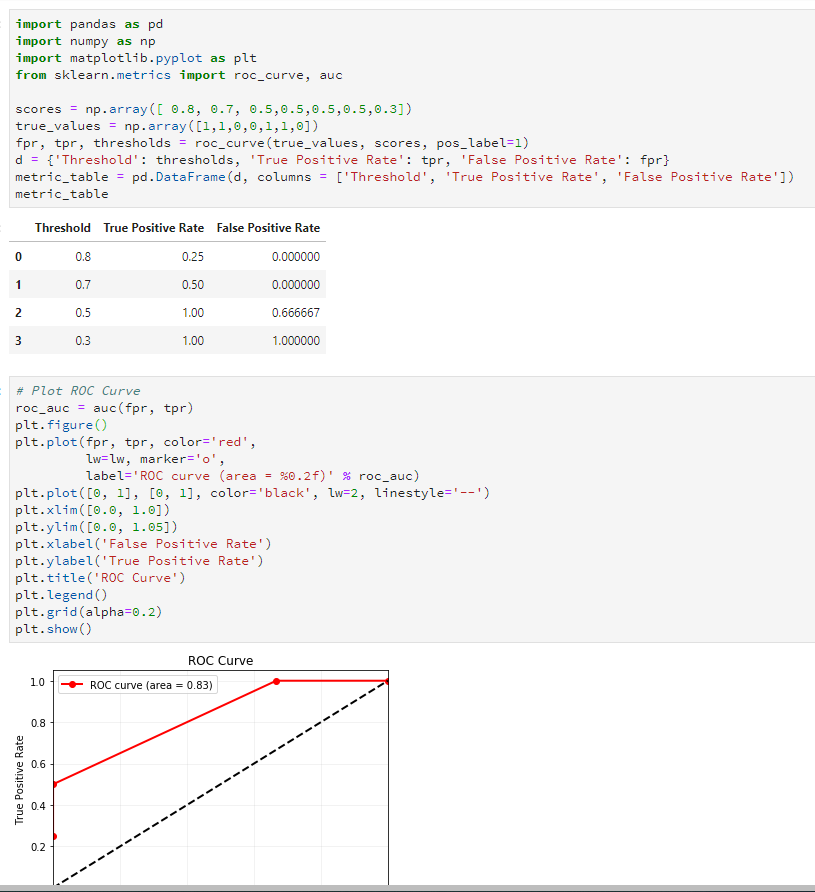
(3)画出最终的ROC曲线和计算AUC值

from sklearn.metrics import auc
AUC=auc(TPRandFPR['FP'],TPRandFPR['TP'])plt.scatter(x=TPRandFPR['FP'],y=TPRandFPR['TP'],label='(FPR,TPR)',color='k')
plt.plot(TPRandFPR['FP'],TPRandFPR['TP'],'k',label='AUC=%0.2f'%AUC)
plt.legend(loc='lower right')plt.title('Receiver Operating Characteristic')
plt.plot([(0,0),(1,1)],'r--')
plt.xlim([-0.01,1.01])
plt.ylim([-0.01,1.01])
plt.ylabel('True positive rate')
plt.xlabel('False positive rate')
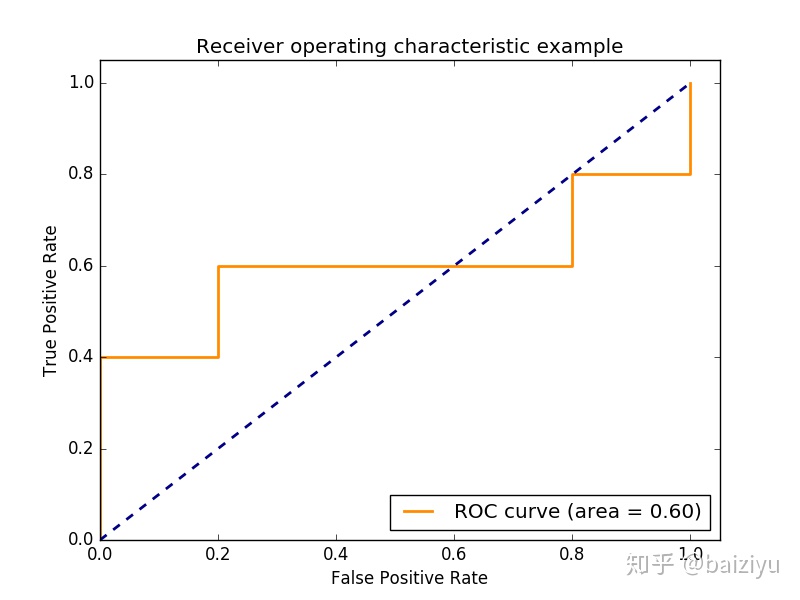
plt.show()

下图的黑色线即为ROC曲线测试样本中的数据点越多，曲线越平滑：

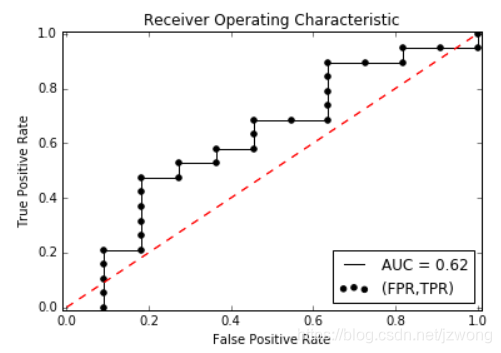
AUC(Area Under roc Curve)，顾名思义就是ROC曲线下的面积，在此例子中AUC=0.62.AUC值越大，说明分类效果越好。