再续FFT：信号的频谱分析

article/2025/8/10 2:09:08

摘自：http://www.ilovematlab.cn/thread-119939-1-1.html
http://www.360doc.com/content/13/1208/18/13670635_335496776.shtml

对于下面这句话该怎么理解？

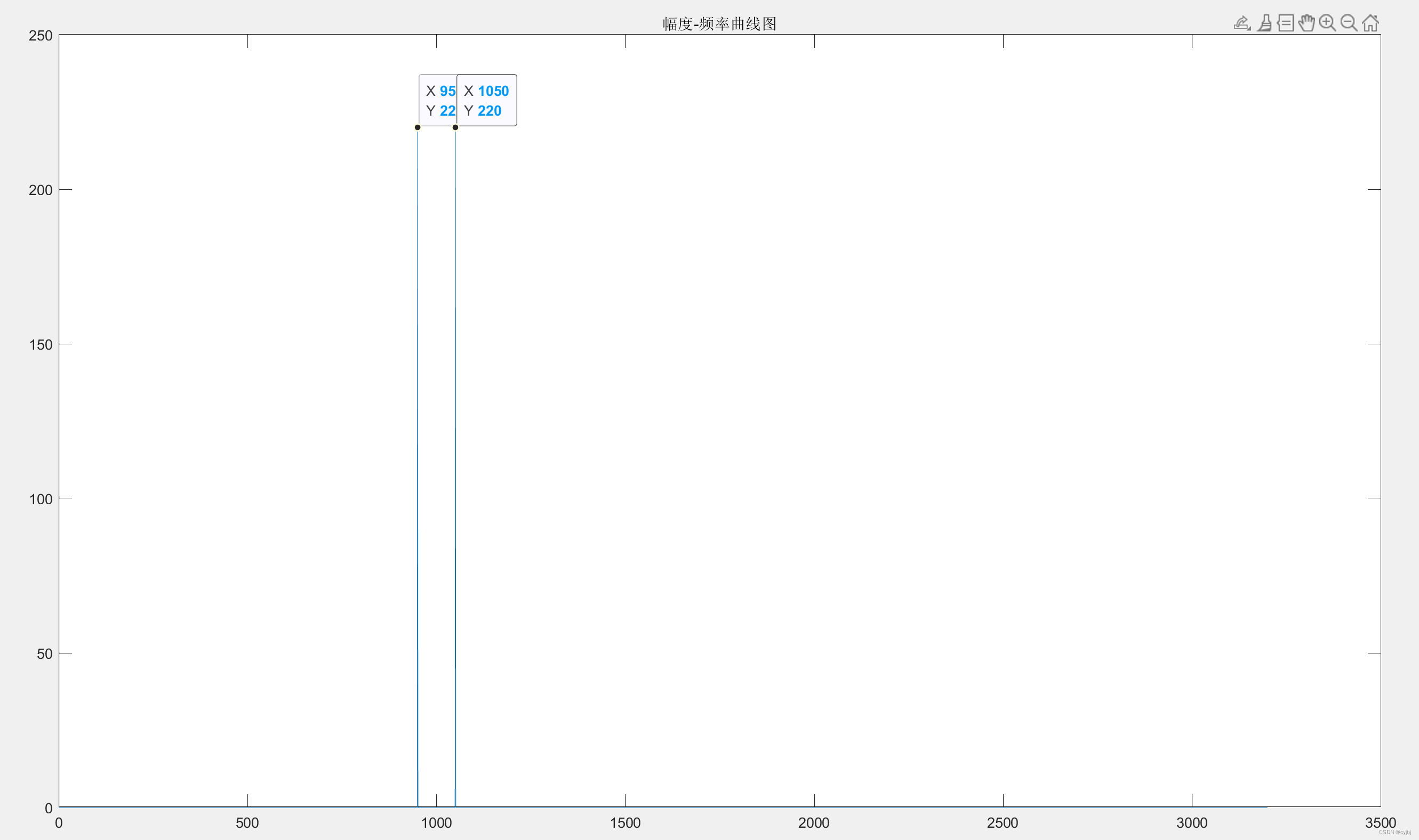
假设采样频率为Fs，信号频率F，采样点数为N。那么FFT之后结果就是一个为N点的复数。每一个点就对应着一个频率点。这个点的模值，就是该频率值下的幅度特性。具体跟原始信号的幅度有什么关系呢？假设原始信号的峰值为A，那么FFT的结果的每个点（除了第一个点直流分量之外）的模值就是A的N/2倍。而第一个点就是直流分量，它的模值就是直流分量的N倍。

思考：一个序列波形，怎样求得峰值及其位置，进而求得周期？

（注：要先进行平滑滤波处理。）

摘自：http://www.ilovematlab.cn/thread-289950-1-1.html

前言：
1）可用[a,b]=max(data)(data是一离散数列)求极大值，但这种方法作用有限，不能找到连续极值。
2）[a,b] = findpeaks(data)：a 对应峰值，b 对应峰值位数。但缺点是只能找波峰值，无法找波谷值。

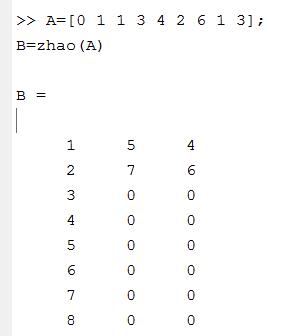
1.自建一个求峰值坐标函数

function A=zhao(M);
global n;
double M;double A;
n=1;
l=length(M);
a=zeros(1,(l-1));b=1:l-1;
A=[b' a' a'];       %对A进行初始化，(n-1)*3型
for i=1:l-1;if(M(i)>M(i+1)&&M(i-1))A(n,2)=i;A(n,3)=M(i);n=n+1;end
end
end

这里写图片描述

继而再求出周期（对于循环序列波形来说）：也就是相邻两个极大值之间的距离。

只需要再提取B的第二列（最高点出现的横坐标位置），做差分。若有负值，将负值及负值之后的全0数据都舍去。然后再将负值前面的s个数据相加再/s即可。

m=(B(:,2));     
p=diff(m);
t=0;
for i=1:l-2if(p(i)>0)t=p(i)+t;s=i;endT=t/s;

2.添注：用matlab函数找序列波形的零点

前言：基本波形绘制

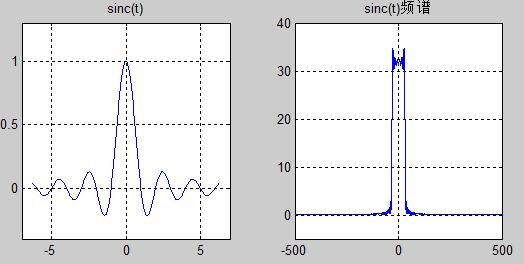
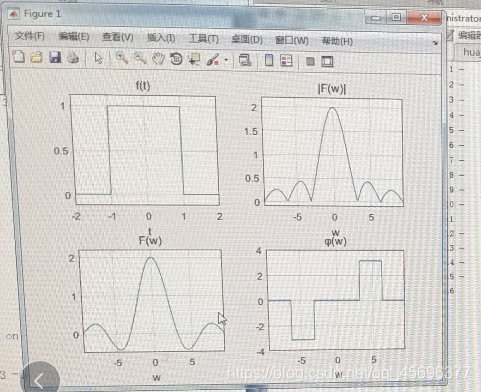
%%%%%%%%绘制在-2pi~2pi区间冲激函数y=sin(t)/t的时域和频域图
clear;
n=400;
delta=4*pi/n;
t=-2*pi:delta:2*pi;
y=sinc(t);      %定义冲激函数
subplot(121);
plot(t,y);axis([-7,7,-0.4,1.3]);
title('sinc(t)');
grid on;
subplot(122);
Y1=fft(y,2048);
Y=fftshift(Y1);
c=-1024:1023;
plot(c,abs(Y));
axis([-500,500,-5,40]);
title('sinc(t)频谱');
grid on;

这里写图片描述

对于fftshift（）；

解释：摘自http://blog.sina.com.cn/s/blog_68f3a4510100qvp1.html

第三段：根据Fourier分析的相关结论，我们知道时域的采样将会造成频域的周期化，该周期为采样频率f_s（即书本上的Fs），我们谱分析是就是观察0~Fs这一段。

由奈奎斯特采样定理可以知道，fs必须≥信号最高频率的2倍才不会发生信号混叠，因此fs能采样到的信号最高频率为fs/2.所以只有f=fs/2范围内的信号才是被采样到的有效信号。那么，在w的范围内，得到的频谱肯定是关于n/2对称的。（所以下文的频谱仪显示窗的频率范围为0~Fs/2，是为了便于观察和分析）

和后面：如果我们不使用fftshift，其变换后的横坐标为0:f_s/(N-1):f_s， 如果使用fftshift命令，0频率分量将会移到坐标中心，这也正是matlab中帮助中心给出的意思：对fft的坐标进行了处理。实际上由于频谱的周期性，我们这样做是合理的，可以接受的。

一.频谱仪的时窗谱线分析

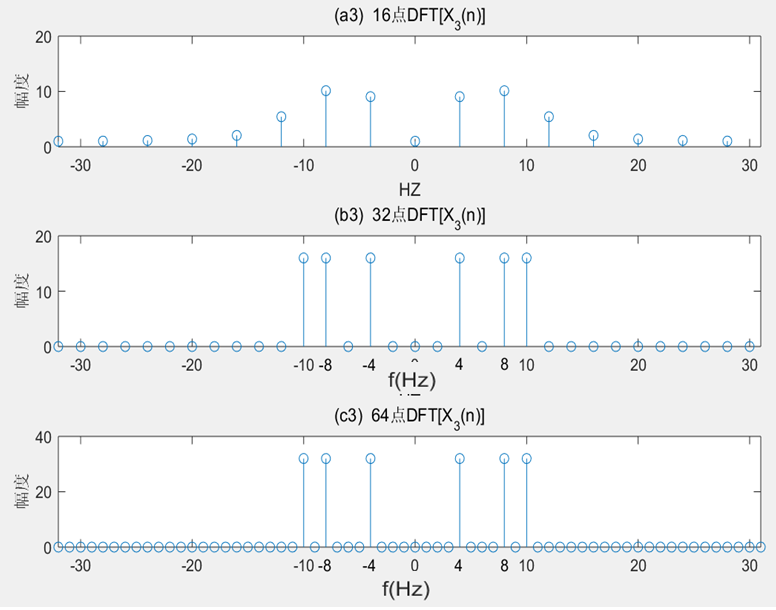
频谱仪用FFT完成数据流从时域到频域的变换。FFT长度为N(一般为2的n次幂)，N的大小，即时窗的长短，决定着频谱仪的频率分辨率，时窗越长，分辨率越高，可以将相隔很近的谱线区分开。

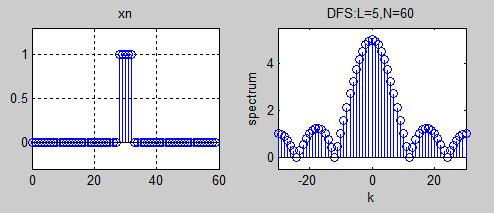
1.用矩阵运算的方法计算方波的DFS（离散傅里叶级数），在60的时窗宽度上方波宽度分别为5和12，并且画出x（n）和DFS（x（n））的杆状图。

clc;
L=5;N=60;
k=[-N/2:N/2];
xn=[zeros(1,(N-L+1)/2),ones(1,L),zeros(1,(N-L-1)/2)];    %方波信号的另一种表示
n=[0:N-1];subplot(221);stem(n,xn);grid;
axis([0,60,-0.3,1.3]);title('xn');p=[0:N-1];
WN=exp(-j*2*pi/N);
nk=n'*p;
WNnk=WN.^nk;
Xk=xn*WNnk;
magXk=abs([Xk(N/2+1:N) Xk(1:N/2+1)]);%   这一段是求和，好好理解（我也不会....）subplot(222);stem(k,magXk);grid
axis([-N/2,N/2,-0.5,5.5]);
xlabel('k');ylabel('spectrum');
title('DFS:L=5,N=60');grid;

这里写图片描述

注：方波的宽度越窄，响应频谱的带宽越宽。如冲激信号的频谱在无线区间上是一恒定值

2.+不同窗函数的频谱分析

a.

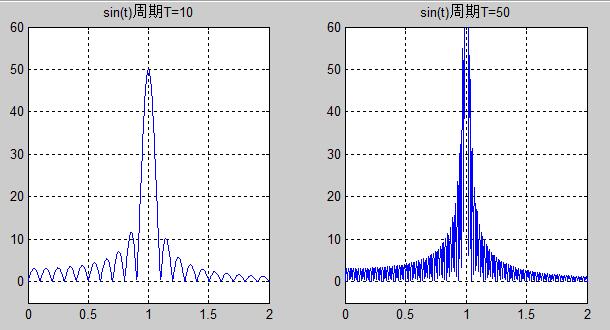
%%%%不同时窗正弦信号频谱的分析
%   设一个1Hz的正弦波，取10和50个周期，都做4096点FFT，比较二者的频谱
clear all;
t=0:0.1:10;
y=sin(2*pi*t);
Y1=fft(y,4096);
Y=fftshift(Y1);
c=[0:2047]/409.6;
subplot(121);
plot(c,abs(Y(2049:4096)));      %谁能告诉我这三行是什么意思吗？如为什么要/409.6，还有y的取值
axis([0,2,-5,60]);
title('sin(t)周期T=10');
grid;t=0:0.1:50;
y=sin(2*pi*t);
Y1=fft(y,4096);
Y=fftshift(Y1);
c=[0:2047]/409;
subplot(122);
plot(c,abs(Y(2049:4096)));
axis([0,2,-5,60]);
title('sin(t)周期T=50');
grid;

这里写图片描述

解释：无限长的正弦信号频谱是一根根垂直于频率轴的垂直线段，有限长的正弦信号等于无限长正弦信号与时窗等长且高度为1的方波的乘积，由卷积定理可知，有限长的正弦信号的频谱等于1/(2*pi)方波的频谱与正弦信号的谱线的卷积。而窄方波的频谱宽，宽方波的频谱窄，故将t取值为50可得到更宽时窗的频谱，且失真较小。

b.加窗函数后的频谱分析。


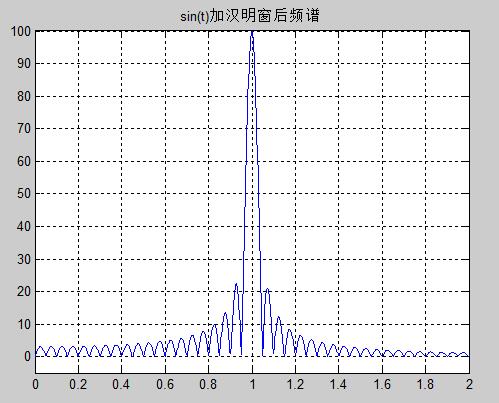
%%%   设一个1Hz的正弦波，取20个周期，求加上窗函数（汉明窗）之后的频谱clear all;
t=0.1:0.1:20;
y=sin(2*pi*t);
w=hamming(200);
y1=y.* w';
y2=fft(y,4096);
y3=fftshift(y2);
c=[0:2047]./409.6;
plot(c,abs(y3(2049:4096)));
axis([0,2,-5,100]);
title('sin(t)加汉明窗后频谱');
grid on;

这里写图片描述

解释：求频谱加不加函窗数的区别：不加窗函数是正弦谱线和矩形窗频谱的卷积，加窗函数是正弦谱线和汉明窗频谱的卷积。

二.周期序列的DFS及DFT

a.基本方波序列

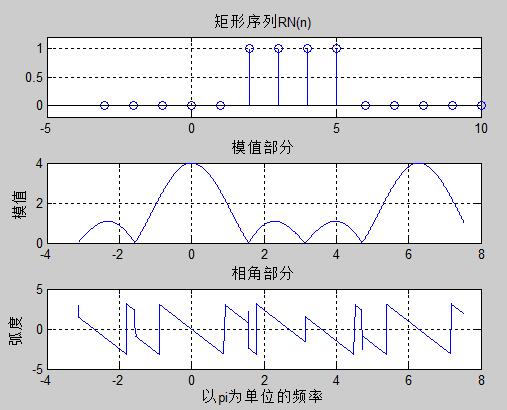
这里写图片描述

%%%%求序列x(n)=RN(n)的X(e.^jw)，并画出序列、模、相角曲线
%矩形序列：起点n0，终点n1，序列为1值区间[ns,nf].clear all;
clc;
n0=input('n0=');n1=input('n1=');ns=input('ns=');nf=input('nf=');
if(n0>=n1|ns>=nf|n0>=ns|nf>=n1)error('输入错误');
end;
n=n0:n1;
x=[zeros(1,ns-n0),ones(1,nf-ns+1),zeros(1,n1-nf)];      %单位阶跃序列产生
subplot(311);stem(n,x);title('矩形序列RN(n)');
axis([-5,10,-0.2,1.2]);grid;k=-500:1200;w=(pi/500)*k;       %[0,pi]段分为501点
X=x*(exp(-j*pi/500)).^(n'*k);       % 用矩阵-向量乘法求DTFT   subplot(312);plot(w,abs(X));grid;
xlabel('');ylabel('模值');title('模值部分');
subplot(313);plot(w,angle(X));grid;
xlabel('以pi为单位的频率');ylabel('弧度');title('相角部分');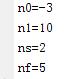

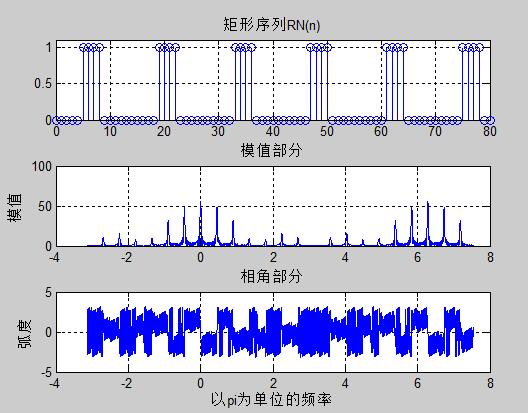
这里写图片描述
这里写图片描述

b.周期序列

这里写图片描述

条件同上，将其以N=8为周期进行周期延拓，得到序列x(n)~.画出DTFT.

%%%%求序列x(n)=RN(n)的X(e.^jw)，并画出序列、模、相角曲线
%矩形序列：起点n0，终点n1，序列为1值区间[ns,nf].clear all;
clc;
n0=input('n0=');n1=input('n1=');ns=input('ns=');nf=input('nf=');
if(n0>=n1|ns>=nf|n0>=ns|nf>=n1)error('输入错误');
end;
n=n0:n1;
x=[zeros(1,ns-n0),ones(1,nf-ns+1),zeros(1,n1-nf)];      %单位阶跃序列产生xtidle=x'*ones(1,n1-n0+1);  %用x转置乘以x的长度大小的全1矩阵。
xtidle=xtidle(:);          % A(:)就是按matlab中的存储顺序，从A(1)到A(end)依次按列排序,第二列接到第一列上，然后依次反复，使A变成一个列向量
xtidle=xtidle';     再转置形成1*（n1-n0+1）^2行矩阵
%%%%%%%%%%%%上面三行就是进行周期延拓的n=0:length(xtidle)-1;subplot(311);stem(n,xtidle);title('矩形序列RN(n)');
axis([0,80,0,1.1]);grid;k=-500:1200;w=(pi/500)*k;       %[0,pi]段分为501点
X=xtidle*(exp(-j*pi/500)).^(n'*k);       % 用矩阵-向量乘法求DTFT   subplot(312);plot(w,abs(X));grid;
xlabel('');ylabel('模值');title('模值部分');
subplot(313);plot(w,angle(X));grid;
xlabel('以pi为单位的频率');ylabel('弧度');title('相角部分');

这里写图片描述

三.FFT实现周期信号的频谱分析（暂略，待补）


http://chatgpt.dhexx.cn/article/R3FrcoOH.shtml

相关文章

实验五 连续信号的频谱分析

实验五 连续信号的频谱分析

目录 一、实验目的二、实验原理1、连续周期信号的傅里叶级数、各次谐波及叠加2、连续周期信号的周期T的变化对频谱的影响3、连续非周期信号的频谱 三、实验内容1、在实验原理1中，绘制加入5次谐波后的波形，根据该仿真图，说明为什么加入5次谐波…
阅读更多...
【信号与系统】（十四）傅里叶变换与频域分析——周期信号的频谱及特点

【信号与系统】（十四）傅里叶变换与频域分析——周期信号的频谱及特点

文章目录 周期信号的频谱及特点1 周期信号的频谱2 单边谱和双边谱的关系3 周期信号频谱的特点4 周期信号的功率 周期信号的频谱及特点 频谱——信号的一种新的表示方法 1 周期信号的频谱 频谱：周期信号分解后，各分量的幅度和相位对于频率的变化&#x…
阅读更多...
信号频谱和傅氏变换

信号频谱和傅氏变换

信号频谱和傅氏变换基本思想： 把一个复杂信号分解成许多简单的正弦信号的叠加,这些正弦信号的频率是已知的，相应的振幅和相位则可由原始信号确定。 周期信号都可以表示成谐波关系的正弦信号的加权和，非周期信号都可以用正弦信号的加权积分来…
阅读更多...
基于FFT的信号频谱分析

基于FFT的信号频谱分析

设计要求 用MATLAB产生正弦波及白噪声信号,并显示各自时域波形图。进行FFT变换,显示各自频谱图。做出两种种信号的均方根图谱,功率图谱,以及对数方均根图谱。用IFFT傅里叶反变换恢复信号,并显示时域波形图 正弦波的信号频谱分析 正弦波源代码 clear all clc %*************…
阅读更多...
近代数字信号处理实验-DFT分析信号的频谱

近代数字信号处理实验-DFT分析信号的频谱

一、实验目的 （1）掌握利用DFT近似计算不同类型信号频谱的原理和方法。 （2）理解误差产生的原因及减小误差的方法。 （3）培养学生自主学习能力，以及发现问题、分析问题和解决问题的能力。 二、…
阅读更多...
Matlab中利用FFT实现信号频谱搬移

Matlab中利用FFT实现信号频谱搬移

目录 Matlab中利用FFT实现信号频谱搬移只有实部的频谱搬移只有虚部的频谱搬移复函数下的频谱搬移 Matlab中利用FFT实现信号频谱搬移 在fft的理论中，fft的频移特性表示为： 也就是说，要想对信号f（t）实现频域的频谱搬移&…
阅读更多...
转|周期矩形脉冲信号频谱及特点

转|周期矩形脉冲信号频谱及特点

周期矩形波信号及其频谱 如图所示信号为脉冲宽度τ，脉冲幅度A，周期为T的周期矩形脉冲信号。 上述周期矩形脉冲信号的傅里叶系数推导可参考占空比任意方波的傅里叶级数展开最终化简可得到下面的表达式。 由此式可得知，该信号频谱谱线大致按照…
阅读更多...
用Matlab求余弦信号的频谱

用Matlab求余弦信号的频谱

如果你是电子信息类专业的学生，一定对频谱这个词听过无数次了，当然求频谱的方法之一就是可以采取快速傅里叶的方法，今天来给大家介绍一种用Matlab对余弦信号求频谱的实际操作。 第一步：构建原始余弦信号 Matlab代码如下&#xf…
阅读更多...
2、信号与频谱

2、信号与频谱

2.1、概述 信号传输的实质：信息传输的过程就是信号变换和处理的过程。如何观察信息传输过程中信号发生了什么变化？ 一种方法是在时域 观察信号波形的变化，另一种方法是在频域观察信号频谱的变化。最常见的基本信号：正弦信号。 2…
阅读更多...
matlab画信号频谱

matlab画信号频谱

为了让大学生活充实一点，多学点东西，我选修了《数字信号处理》。现在充实得不要不要的。 clc close all clear%参数设置% Fs 1000; % Sampling frequency T 1/Fs; % Sampling period L 1500; …
阅读更多...
利用DFT分析信号频谱【信号与系统二】

利用DFT分析信号频谱【信号与系统二】

利用DFT分析信号频谱 1. 利用FFT分析信号频谱2. 产生一个淹没在噪声中的信号x(t)，分析信号的频谱3. 利用有限项分析三角波信号4. 利用频域分析方法，重新对第一次实验时的含噪信号进行滤波处理5. 通过频谱分析，识别电话拨号音的电话号码6. 试着…
阅读更多...
信号与系统（3）——周期矩形脉冲信号频谱及特点

信号与系统（3）——周期矩形脉冲信号频谱及特点

周期矩形脉冲 如图所示信号为脉冲宽度τ，脉冲幅度A，周期为T的周期矩形脉冲信号。 傅里叶变换推导 上述周期矩形脉冲信号的傅里叶系数推导方式如下： 由此式可得知，该信号频谱谱线大致按照采样函数（Sa(t)）…
阅读更多...
冲激信号的卷积性质采样信号频谱的周期性延拓

冲激信号的卷积性质采样信号频谱的周期性延拓

文章目录 1. 冲激信号的卷积2. 性质:3. 仿真验证： 1. 冲激信号的卷积 由冲激信号的卷积性质可知：冲激信号具有显像性。 任何信号对单位冲激函数的卷积等于该信号本身，那么单位冲激函数就相当于是一种“显像”信号，当冲激函数对冲激…
阅读更多...
Matlab使用fft画出信号频谱（详细注释）

Matlab使用fft画出信号频谱（详细注释）

做雷原作业，需要对信号进行频谱分析，网上一搜太乱了，很多不是我想要的，特此整理。 DSP还没学到fft，就不对fft原理进行详细解释了，直接上代码。 fs500;%采样率 f15;%信号频率 f210;%信号频率 T1;%时宽1s nr…
阅读更多...
连续信号频域分析：功率信号的频谱与能量信号频谱密度

连续信号频域分析：功率信号的频谱与能量信号频谱密度

频域分析： 周期信号非周期信号频谱(离散)频谱密度(也称频谱，连续）功率谱密度能量谱密度 周期信号and非周期信号幅度谱都是偶函数。 一、功率(周期)信号的频谱 认为周期信号为功率信号、非周期信号为能量 信号 1.1周期信号的虚指数/三角傅里…
阅读更多...
FFT_频谱分析（数字信号处理）

FFT_频谱分析（数字信号处理）

~~ 如果有什么问题可以在我的个人博客留言 ，我会及时回复。欢迎来访交流 ~~ FFT_频谱分析（数字信号处理） （一）实验原理 用FFT对信号作频谱分析是学习数字信号处理的重要内容。经常需要进行谱分析的信号是模拟信号和时…
阅读更多...
数字信号处理(matlab)——FFT对信号频谱分析

数字信号处理(matlab)——FFT对信号频谱分析

FFT频谱分析法 频谱分辨率D FFT能够实现的频率分辨率是2pi/N 要求2pi/N≤D 误差主要来自于用FFT做频谱分析时，得到的是离散谱，但是信号是连续谱，只有当N较大时，离散谱的包络才能逼近离散谱，因此N要大一些。 为了方便读…
阅读更多...
matlab信号频谱分析FFT详解

matlab信号频谱分析FFT详解

前言 做OFDM通信少不了频谱分析，基带信号DA后的频谱，以及基带数字上变频后的DA信号都要频谱分析。我觉得其实做任何工程都是这样，先规定实施方案，然后仿真成功，再实际开发，不过也可以一边开发，…
阅读更多...
信号与频谱

信号与频谱

身为一名通信专业出生的我，居然淡忘了信号的基本知识，今天带大家回顾一下，通俗易懂。 信号(singal)简介 我们在生活中经常遇到信号。比如说，股票的走势图，心跳的脉冲图等等。在通信领域，无论是的GPS、手机…
阅读更多...
【信号与系统】笔记（3-2）信号的频谱与傅里叶变换（一图看懂傅里叶变换）

【信号与系统】笔记（3-2）信号的频谱与傅里叶变换（一图看懂傅里叶变换）

Author：AXYZdong 自动化专业 工科男 有一点思考，有一点想法，有一点理性！ 文章目录 一图看懂傅里叶变换前言一、周期信号的频谱1、周期信号频谱的相关概念2、周期信号频谱的特点3、谱线的结构与波形参数的关系 二、非周期信号的频谱…
阅读更多...
推荐文章

Copyright @ 2022~2023