一: Spfa算法分析

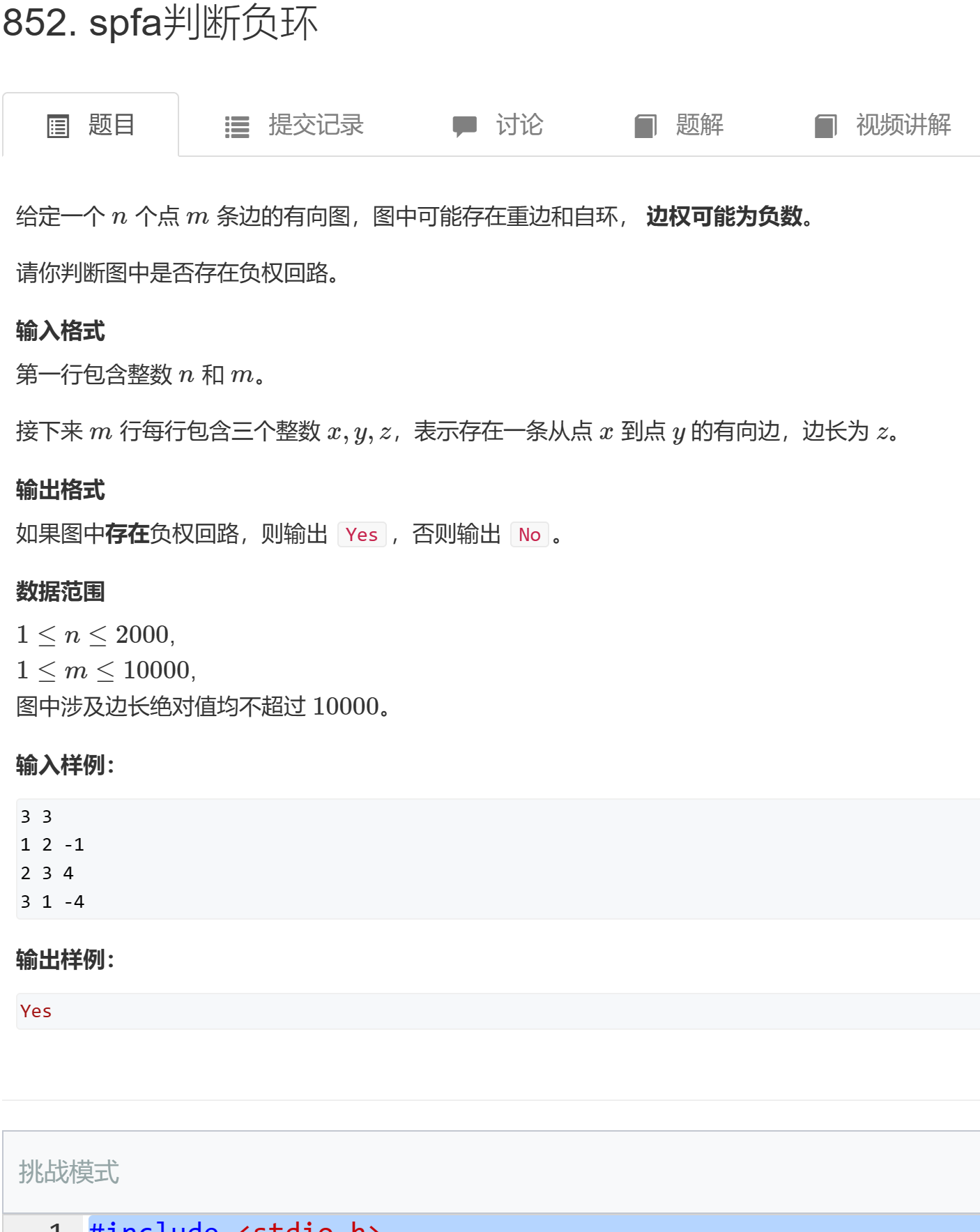
 1. 问题介绍：



 2. 问题分析：
 当我们遇到单源最短路+边权为负值问题时这时候该如何处理呢？
 其实我们现在就可以使用Floyd()算法了，我们可以从两个方面来理解这个算法.
 第一个方面从Bellman_ford()算法来理解,Spfa算法其实就是对Bellman-ford算法的一个优化，因为Bellman_ford算法每次其实都是对所有边的一个松弛过程，但其实我们可以优化为只去松弛那些距离变小的点并将其放入队列当中继续松弛即可。
 其实有一个更好理解的方式，Spfa算法其实就和Dijkstra算法类似，不过的是Dijkstra算法每次都可以确定一个最优解，而Spfa无法确定，所以Spfa可以就看作从一个点开始让整个图不断优化，可以优化就又从那个点开始继续优化直至优化到这个图内所有点都无法再去优化其他点(即所有点达到最优解)。
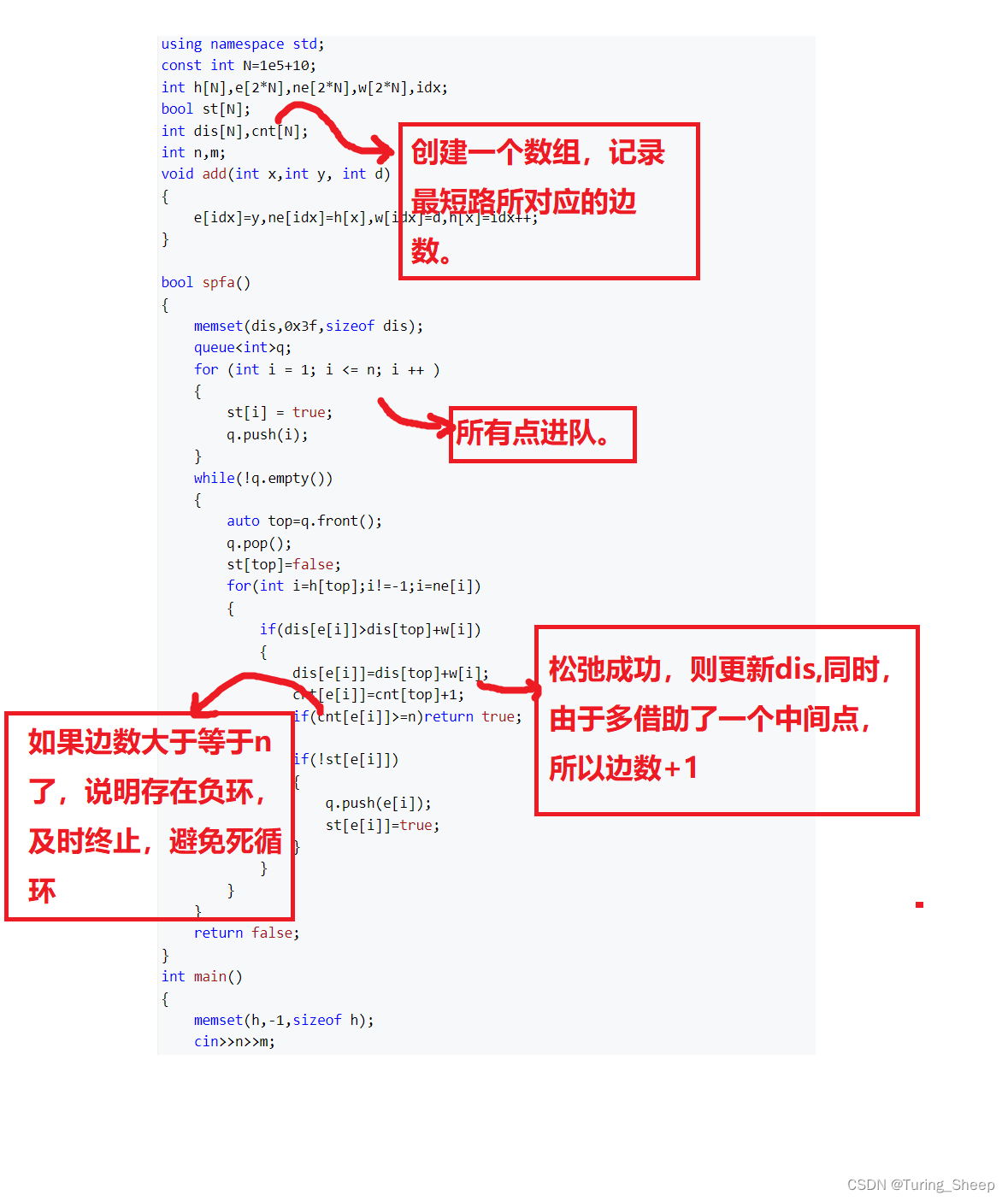
 负环判断：先让所有点都进入队列(相当于引入一个虚拟点到所有点)，然后同时从所有点开始去走，同时记录走到当前点所经过得边数，当边数 >= n结点数量的时候，我们就可以确认必定出现负环，因为经过了n个结点则代表一定经过了n + 1条边.


 3. 算法细节对比：
  a.相同点：算法格式和Dijkstra算法类似
  b.不同点：
  Dijkstra算法使用优先队列, Spfa使用一般队列即可。
  Dijkstra算法每次选取出来的值即是最优解，其状态st[ ] 表示是否已经选取，且状态不可逆 false 变为 true 不可倒退。
  Spfa算法因为可能此点会被其他点再次优化所以其 状态st[ ]表示的是是否进入队列当中，可能会再次出队列所以要同步更新st[ ] 状态。


 4. 算法总结：
 时间复杂度: 最优 O(m) ,最差退回bellman-ford O(n m)
 处理问题: 单源最短路 + 权值为负

二: 代码分析

a.注意时刻保持st[ ]状态和点是否在队列当中一致

	// 出队列int u = q.front();q.pop();// 进队列st[u] = false;q.push(j);st[j] = true;

b.可以利用cnt[ ]数组记录离源点边数，当边数>=n 证明存在负环

for(int i = h[u]; ~ i; i = ne[i] ){int j = e[i];if(dis[j] > dis[u] + w[i] ){dis[j] = dis[u] + w[i];cnt[j] = cnt[u] + 1;if (cnt[j] >= n) puts("存在负环")if(!st[j]){q.push(j);st[j] = true;}}
}

c.完整代码

#include<iostream>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
const int N = 1e5 + 10, inf = 0x3f3f3f3f;
int h[N], e[N], ne[N], w[N], idx = 0;
int n, m, dis[N];
bool st[N];
void add(int x, int y, int z){e[idx] = y, ne[idx] = h[x], w[idx] = z, h[x] = idx ++;
}
void spfa(){queue<int> q;q.push(1);dis[1] = 0;st[1] = true;/* 判断整个图是否有负环，先全部入队列for(int i = 1; i <= n; i ++ ){q.push(i);st[i] = true;}*/while(!q.empty() ){//先初始化放入初始源点int u = q.front();q.pop();st[u] = false;//将此点优化过的点再次放入队列，重复这个过程直至队列为空即可for(int i = h[u]; ~ i; i = ne[i] ){int j = e[i];if(dis[j] > dis[u] + w[i] ){dis[j] = dis[u] + w[i];// cnt[j] = cnt[u] + 1;// if (cnt[j] >= n) puts("存在负环")if(!st[j]){q.push(j);st[j] = true;}}}}}int main(){memset(h, -1, sizeof(h) );memset(dis, 0x3f, sizeof(dis) );cin >> n >> m;for(int i =0; i < m; i ++ ){int x, y, z;cin >> x >> y >>z;add(x, y, z);}spfa();if(dis[n] == inf) puts("impossible");else cout << dis[n] << endl;
}